Half Of 1 1/2 Cups
cibeltiagestion
Sep 04, 2025 · 5 min read
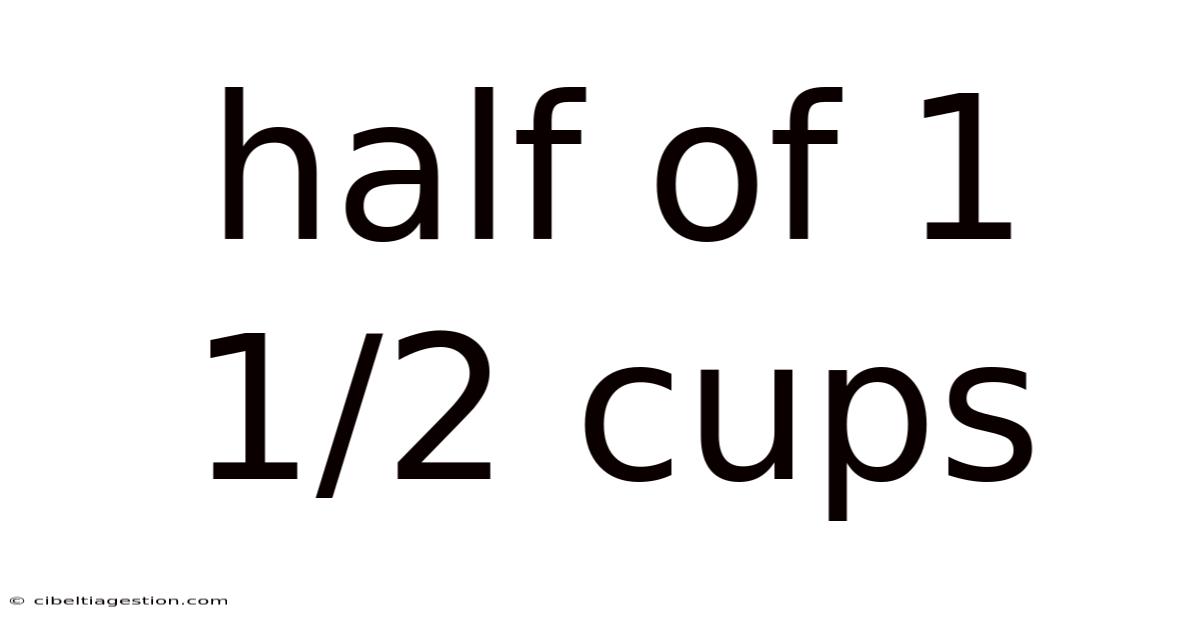
Table of Contents
Decoding the Mystery: Half of 1 1/2 Cups
Finding half of a measurement can seem deceptively simple, but when dealing with fractions like 1 ½ cups, it can become a bit trickier. This article will guide you through calculating half of 1 ½ cups, providing a step-by-step process, explanations of the underlying mathematics, and answering frequently asked questions. Understanding this seemingly basic concept can prove invaluable in baking, cooking, and various other applications requiring precise measurements. We'll explore different approaches, ensuring you feel confident in tackling similar fraction-based measurements in the future.
Understanding the Problem: Half of 1 ½ Cups
The core problem is calculating half of 1 ½ cups. This involves working with mixed numbers (a whole number and a fraction). To find half, we need to convert the mixed number into an improper fraction, making the calculation much easier. This process allows us to apply basic fractional arithmetic principles consistently and accurately. Many everyday tasks, from following a recipe to adjusting medication dosages (under professional guidance), benefit from this skill.
Method 1: Converting to an Improper Fraction
This is the most common and arguably easiest method. Let's break it down:
-
Convert the mixed number to an improper fraction: 1 ½ cups can be written as (1 + ½) cups. To convert this to an improper fraction, we multiply the whole number (1) by the denominator (2) and add the numerator (1). This result becomes the new numerator, while the denominator remains the same. Therefore, 1 ½ cups becomes 3/2 cups.
-
Find half of the improper fraction: To find half, we multiply the improper fraction by ½: (3/2) * (1/2) = 3/4.
-
Result: Half of 1 ½ cups is 3/4 of a cup.
Method 2: Working with Whole and Fractional Parts Separately
This method involves dividing the whole number and fractional part separately, then combining the results.
-
Divide the whole number: Half of 1 cup is ½ cup.
-
Divide the fractional part: Half of ½ cup is ¼ cup.
-
Combine the results: Adding the results together, we get ½ cup + ¼ cup. To add these fractions, we need a common denominator, which is 4. So, ½ cup becomes 2/4 cup. Adding 2/4 cup and ¼ cup gives us 3/4 cup.
-
Result: Again, half of 1 ½ cups is 3/4 of a cup.
Visual Representation: Understanding Fractions
Imagine a measuring cup. A full cup represents 1. Divide this cup into two equal halves; each half represents ½. Now, if we have 1 ½ cups, we have a full cup and half a cup. Dividing that in half means splitting the full cup into two halves (resulting in two ½ cups) and the additional ½ cup into two ¼ cups. This gives us a total of three ¼ cups, or 3/4 of a cup. Visualizing the process can greatly enhance understanding, particularly for those who are visually-oriented learners.
Practical Applications: Beyond the Kitchen
While initially seeming limited to cooking and baking, understanding how to halve mixed numbers has broad practical implications. For instance:
- Baking & Cooking: Adjusting recipes for smaller portions requires accurate fractional calculations.
- Construction & DIY: Precise measurements are essential for projects like carpentry, plumbing, and electrical work.
- Gardening: Calculating the correct amount of fertilizer or pesticide based on package instructions often involves fractional measurements.
- Sewing & Crafting: Accurate fabric or yarn measurements are crucial for creating precise garments or other crafts.
- Medicine (under professional guidance): In some instances, adjusting medication dosages might involve working with fractions. Always consult with a healthcare professional before making any changes to prescribed medications.
Scientific Explanation: The Mathematics of Fractions
The core mathematical principle at play here is the multiplication of fractions. When we multiply two fractions, we multiply the numerators together and the denominators together. Converting the mixed number to an improper fraction simplifies the process, allowing for a straightforward multiplication. This aligns with fundamental algebraic principles related to fractional arithmetic. A strong grasp of these principles extends beyond this specific problem, making you more comfortable with various fraction-based calculations in various contexts.
Frequently Asked Questions (FAQ)
Q1: What if I don't have a measuring cup that shows ¼ cups?
A1: You can use other tools. A tablespoon is approximately 1/16 of a cup, and there are 16 tablespoons in a cup. Therefore, 3/4 of a cup equals 12 tablespoons. You can measure 12 tablespoons using a tablespoon measuring spoon. Alternatively, you could use a liquid measuring cup and estimate 3/4 of a cup visually. Practice will improve your estimation skills.
Q2: Can I use a calculator to solve this?
A2: Yes, absolutely! Most calculators have fraction functionalities. Inputting the fraction 3/2 and then multiplying by 0.5 (or 1/2) will give you the decimal equivalent of 0.75, which represents 3/4. Using a calculator is particularly helpful for more complex fraction calculations.
Q3: What are some common errors to avoid?
A3: A common error is forgetting to convert the mixed number to an improper fraction before performing the calculation. This can lead to inaccurate results. Another error is incorrectly adding or subtracting fractions without finding a common denominator.
Q4: How can I improve my skills in working with fractions?
A4: Practice regularly! Start with simple fraction problems and gradually increase the complexity. There are many online resources and workbooks available to help you improve your skills. Understanding the underlying principles of fraction arithmetic is key to success.
Q5: Is there a way to check my answer?
A5: Yes, you can double your answer to verify if it matches the original amount. If you have 3/4 of a cup, doubling it (multiplying by 2) should result in 1 ½ cups (which is 3/2, the improper fraction form of 1 ½ cups).
Conclusion: Mastering Fractions for Everyday Success
Mastering the skill of calculating fractions, particularly halving mixed numbers, is a valuable life skill that extends far beyond the kitchen. By understanding the underlying mathematical principles and employing the methods discussed, you can confidently tackle similar calculations in various contexts. Remember that practice is key. Start with the basic method of converting to an improper fraction, and then experiment with the alternative methods to find the approach that works best for you. With a little practice, you'll soon be comfortable navigating the world of fractions with ease and accuracy. This empowers you to approach recipes, DIY projects, and various other tasks with greater precision and confidence, proving that understanding simple mathematical concepts can indeed lead to significant practical benefits.
Latest Posts
Latest Posts
-
Noble Gas Configuration For Barium
Sep 04, 2025
-
What Is 25 Of 47
Sep 04, 2025
-
Gcf Of 96 And 80
Sep 04, 2025
-
How Many Ounces 1 3 Cup
Sep 04, 2025
-
Where Does Cellular Respiration Occur
Sep 04, 2025
Related Post
Thank you for visiting our website which covers about Half Of 1 1/2 Cups . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.