Half Of 2 1 2
cibeltiagestion
Sep 02, 2025 · 4 min read
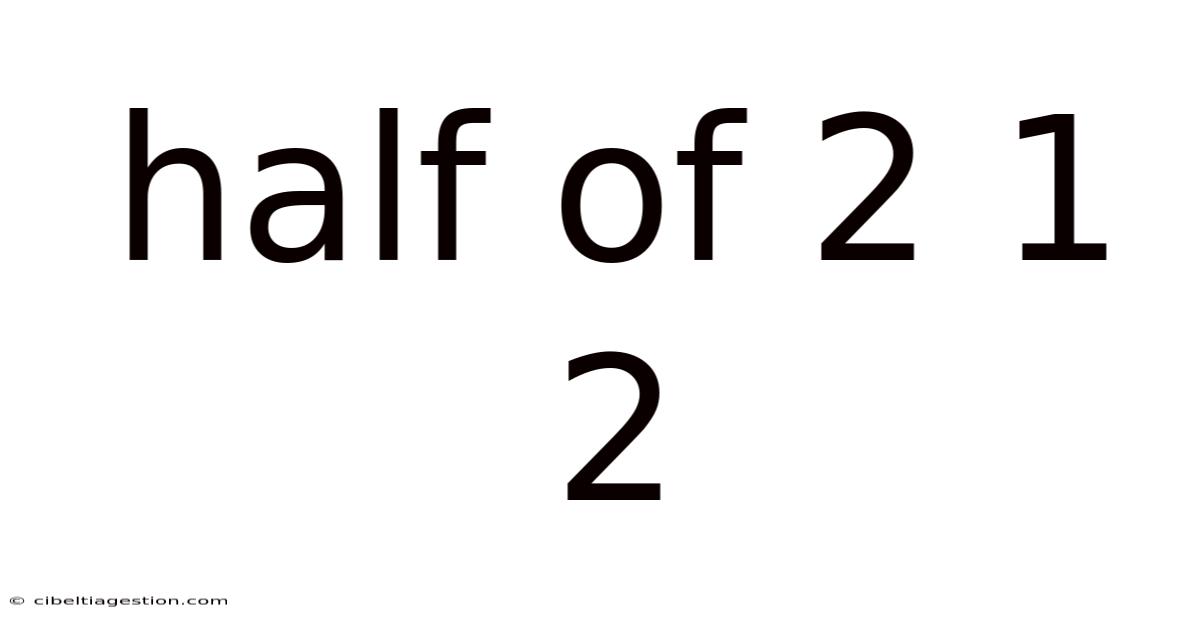
Table of Contents
Decoding "Half of 2 1 2": A Deep Dive into Mathematical Interpretation and Problem-Solving
This article explores the multifaceted interpretation and solution to the seemingly simple problem: "half of 2 1 2". The ambiguity inherent in this phrase highlights the crucial role of mathematical notation and precision in problem-solving. We will unpack various interpretations, delve into the underlying mathematical principles, and address common misconceptions. This comprehensive guide will equip you with the tools to tackle similar ambiguous problems confidently.
Introduction: The Ambiguity of the Problem
The phrase "half of 2 1 2" is deliberately ambiguous. The lack of clear mathematical operators between the numbers leaves room for several interpretations. This ambiguity isn't a flaw; it's an opportunity to examine the importance of precise mathematical language and the different ways we can approach a problem with seemingly limited information. Understanding how to interpret and solve such problems builds critical thinking and problem-solving skills crucial in various fields, from basic arithmetic to advanced mathematics and even programming.
Interpretation 1: "Half of 212"
The most straightforward interpretation treats "2 1 2" as a single number, two hundred and twelve. In this case, the problem becomes finding half of 212.
Solution:
Half of 212 is calculated as 212 / 2 = 106.
Explanation: This interpretation relies on the common understanding of number representation. The digits are concatenated to form a single integer. Dividing this integer by two gives the straightforward answer. This is likely the interpretation most people will initially consider.
Interpretation 2: "Half of (2 + 1 + 2)"
Another interpretation involves treating "2 1 2" as a sum of three individual numbers: 2, 1, and 2.
Solution:
- Sum the numbers: 2 + 1 + 2 = 5
- Find half of the sum: 5 / 2 = 2.5
Explanation: This approach involves separating the digits and performing addition before finding the half. This interpretation demonstrates the importance of understanding the order of operations.
Interpretation 3: "Half of (2 * 1 * 2)"
A less likely but mathematically valid interpretation involves viewing "2 1 2" as representing a product.
Solution:
- Multiply the numbers: 2 * 1 * 2 = 4
- Find half of the product: 4 / 2 = 2
Explanation: This interpretation shows that the same set of numbers can yield a different result depending on the mathematical operation applied. This highlights the need for explicit operators in mathematical expressions to remove ambiguity.
Interpretation 4: Introducing Possible Operations: A Deeper Dive
The lack of explicit operators encourages exploration of various combinations. Let's assume the use of addition, subtraction, multiplication, and division. We could construct expressions to find different results. For example:
- (2 + 1) / 2 + 2 = 3.5 This expression uses both addition and division.
- 2 * (1 + 2) / 2 = 3 This one uses multiplication, addition, and division.
- 2 - 1 + 2 / 2 = 3 Illustrates the importance of order of operations (PEMDAS/BODMAS).
These examples demonstrate the limitless possibilities when operators aren't specified. The resulting answer would depend entirely on the assumptions made about the implied operation between the numbers.
The Importance of Mathematical Notation
The ambiguity of "half of 2 1 2" underscores the paramount importance of precise mathematical notation. Clear operators (+, -, ×, ÷) and parentheses are essential for ensuring that a mathematical expression has only one interpretation. Without them, multiple interpretations are possible, leading to different solutions. This lack of clarity can lead to significant errors, especially in complex calculations or programming contexts where precise instructions are crucial.
Extending the Concept: Similar Ambiguous Problems
The problem "half of 2 1 2" is a simplified illustration of a broader class of ambiguous mathematical problems. Similar puzzles involving sequences of numbers without explicit operators frequently appear in math puzzles and brain teasers. These often rely on creative interpretation and exploring potential relationships between the numbers to find a solution.
Addressing Common Misconceptions
A frequent misconception is that there's only one correct answer. The inherent ambiguity of the problem means that multiple solutions are possible, each valid within its own interpretative framework. The key isn't finding the "correct" answer but rather understanding the different valid interpretations and the reasoning behind them.
Conclusion: The Power of Precise Language and Critical Thinking
The seemingly simple problem "half of 2 1 2" serves as a powerful lesson in the importance of precise mathematical language and critical thinking. The ambiguity inherent in the phrase highlights the need for clear notation and the multiple ways a problem can be interpreted. By exploring different interpretations and their corresponding solutions, we develop a deeper understanding of mathematical principles and enhance our problem-solving abilities. This exercise is not just about finding an answer; it's about cultivating the skills to tackle ambiguous situations and appreciate the importance of clear communication in mathematics and beyond. The lesson extends to various fields, emphasizing the need for unambiguous instructions and precise communication to avoid errors and ensure clarity.
Latest Posts
Latest Posts
-
How Long Is A Sandbox
Sep 02, 2025
-
20 Degrees C In F
Sep 02, 2025
-
Ounces In Pounds How Many
Sep 02, 2025
-
Solve The Given Exponential Equation
Sep 02, 2025
-
Longest Coastline In South America
Sep 02, 2025
Related Post
Thank you for visiting our website which covers about Half Of 2 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.