Half Of 2 2 3
cibeltiagestion
Sep 08, 2025 · 5 min read
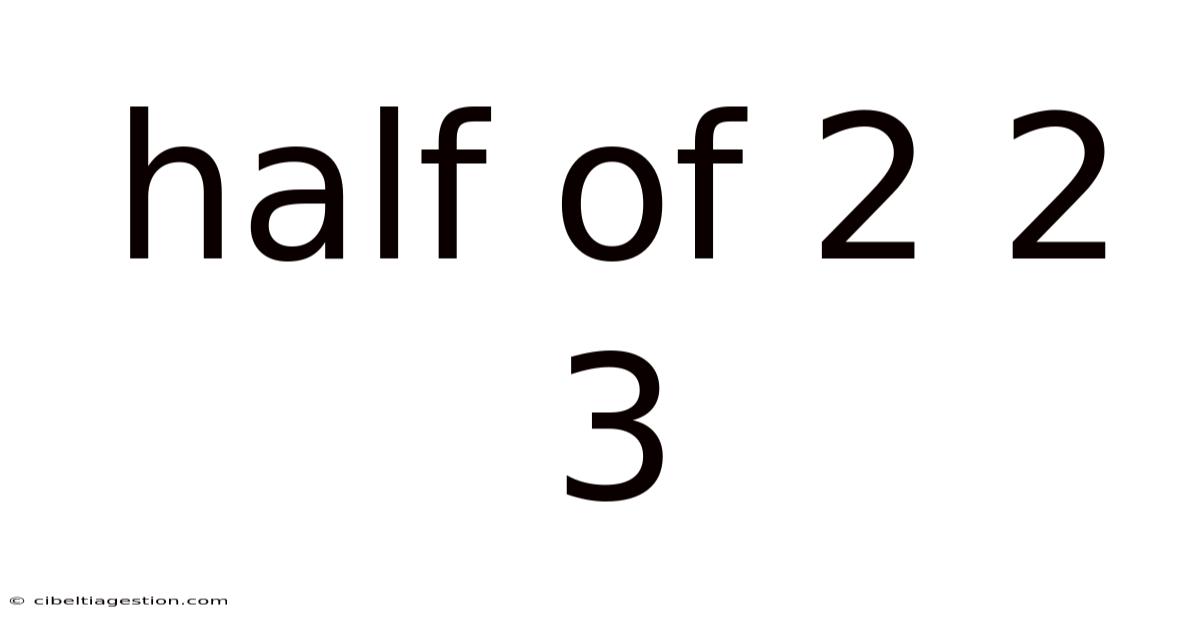
Table of Contents
Decoding "Half of 2 2 3": Exploring Mathematical Ambiguity and Problem-Solving
The seemingly simple phrase "half of 2 2 3" presents a fascinating challenge in mathematical interpretation. Its ambiguity highlights the importance of precise notation and the multiple ways we can approach a problem. This article will delve into the various interpretations of this phrase, explore the underlying mathematical principles, and offer a structured approach to solving similar ambiguous problems. We'll examine the order of operations, different interpretations of the phrasing, and finally, offer some broader insights into mathematical thinking.
Understanding the Ambiguity: Why "Half of 2 2 3" is Tricky
The core issue lies in the lack of explicit operators between the numbers. Is "2 2 3" a concatenation of digits representing a single number (223), or does it imply mathematical operations between them? This ambiguity necessitates careful consideration of the possible interpretations and the application of mathematical rules.
Potential Interpretations and Solutions
Let's explore the most plausible interpretations of "half of 2 2 3":
1. Interpretation 1: "Half of (223)"
This is perhaps the most straightforward interpretation. It assumes "2 2 3" represents the single number 223. Therefore, the problem becomes:
- Half of 223 = 223 / 2 = 111.5
This interpretation directly addresses the phrase "half of" and treats the remaining digits as a single entity. It's a simple division problem and yields a clear, unambiguous answer.
2. Interpretation 2: "Half of (2 + 2 + 3)"
This interpretation assumes addition is implied between the numbers. The problem then becomes:
- Half of (2 + 2 + 3) = Half of 7 = 7 / 2 = 3.5
Here, we've applied the order of operations, performing the addition within the parentheses first, before calculating the half. This interpretation is also relatively straightforward, assuming an implied addition operation.
3. Interpretation 3: Exploring Other Possible Operations
We could, theoretically, consider other mathematical operations like multiplication or a combination of operations. However, without explicit operators, these interpretations become less likely and often lead to multiple solutions depending on the assumed order of operations. For instance:
- Scenario A: (2 x 2) + 3 = 7; Half of 7 = 3.5
- Scenario B: 2 + (2 x 3) = 8; Half of 8 = 4
- Scenario C: (2 + 2) x 3 = 12; Half of 12 = 6
These scenarios highlight the importance of clear notation. The absence of explicit operators introduces considerable ambiguity, leading to multiple valid (depending on the assumptions) mathematical solutions.
The Importance of Order of Operations (PEMDAS/BODMAS)
The order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), is crucial in evaluating mathematical expressions. It dictates the sequence in which operations should be performed to obtain a consistent and unambiguous result. The ambiguity in "half of 2 2 3" arises precisely because the order of operations isn't explicitly defined.
Solving Ambiguous Mathematical Problems: A Structured Approach
When faced with ambiguous mathematical problems like this, a structured approach is essential:
-
Identify the Ambiguity: Clearly define the source of ambiguity. In this case, it's the lack of explicit operators between the numbers.
-
Explore Possible Interpretations: Systematically consider all plausible interpretations, as we did above. List each interpretation and its corresponding mathematical expression.
-
Apply Order of Operations (If Applicable): If an interpretation involves multiple operations, apply the order of operations consistently to reach a unique solution for that interpretation.
-
State Assumptions: Clearly state any assumptions made during the problem-solving process. For instance, "Assuming '2 2 3' represents the number 223," or "Assuming addition is implied between the numbers."
-
Present Multiple Solutions (If Necessary): If multiple interpretations lead to different valid solutions, present them all, clearly indicating the assumptions made for each.
-
Highlight the Importance of Clear Notation: Conclude by emphasizing the importance of precise mathematical notation to avoid ambiguity and ensure clear communication of mathematical ideas.
Expanding the Understanding: Beyond "Half of 2 2 3"
This seemingly simple problem touches upon fundamental concepts in mathematics:
-
The Power of Notation: The example underscores the critical role of precise notation in preventing ambiguity and facilitating clear communication of mathematical ideas. Ambiguous notation can lead to multiple interpretations and potentially incorrect solutions.
-
Interpretative Skills: Solving such problems requires strong interpretative skills. We must analyze the language used and consider various possibilities based on the context and common mathematical conventions.
-
Critical Thinking: The problem encourages critical thinking by forcing us to consider different perspectives and make informed decisions based on the available information (or lack thereof).
-
Problem-Solving Strategies: Tackling the problem involves applying systematic problem-solving strategies: identifying the problem, exploring possibilities, applying relevant rules, and stating assumptions.
Frequently Asked Questions (FAQs)
Q: What is the definitive answer to "half of 2 2 3"?
A: There's no single definitive answer due to the inherent ambiguity in the phrasing. The answer depends on the interpretation of "2 2 3" and the assumed operations.
Q: Why is this problem considered ambiguous?
A: It's ambiguous because there are no explicit mathematical operators (+, -, *, /) between the numbers. This lack of clarity allows for multiple valid interpretations, leading to different answers.
Q: How can I avoid similar ambiguity in my own mathematical writing?
A: Always use clear and explicit mathematical notation. Use parentheses to group terms, specify the operations clearly, and avoid relying on implied operations.
Conclusion: Embracing Mathematical Ambiguity
The seemingly simple phrase "half of 2 2 3" serves as a valuable lesson in the importance of precise mathematical notation and the power of careful interpretation. It highlights the need for clear communication and systematic problem-solving strategies when tackling ambiguous problems. By exploring the various interpretations and applying a structured approach, we can not only find multiple solutions but also deepen our understanding of fundamental mathematical concepts. This exercise encourages critical thinking and reinforces the crucial role of precise language in mathematics. The ambiguity, far from being a flaw, presents a unique opportunity to hone our problem-solving skills and appreciate the nuances of mathematical expression.
Latest Posts
Latest Posts
-
Is Cartel Masculine Or Feminine
Sep 09, 2025
-
Prime Mover Of Back Extension
Sep 09, 2025
-
Edmentum Mastery Test Answers English
Sep 09, 2025
-
Mi Madre Preparo La Comida
Sep 09, 2025
-
Is Length Or Width First
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Half Of 2 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.