Half Of 2 3 8
cibeltiagestion
Sep 06, 2025 · 5 min read
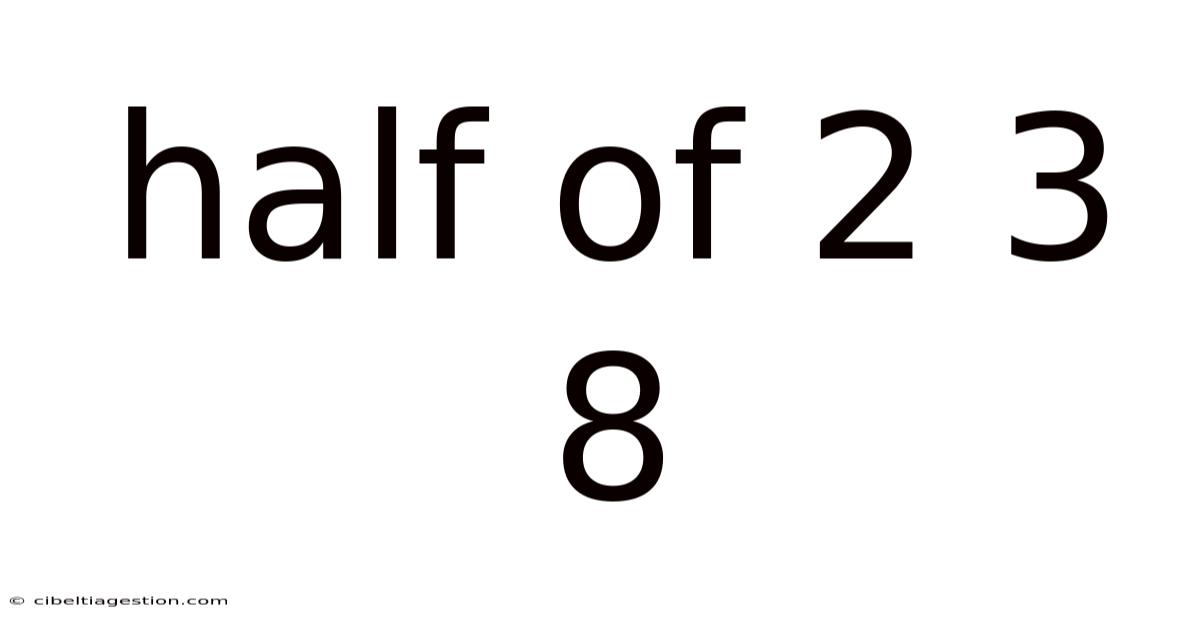
Table of Contents
Decoding "Half of 2, 3, and 8": A Deep Dive into Fractions, Decimals, and Practical Applications
Finding "half of" a number is a fundamental concept in mathematics, crucial for understanding fractions, decimals, and a wide range of real-world applications. This article will explore the seemingly simple task of calculating half of 2, 3, and 8, delving into the underlying principles and extending the concept to more complex scenarios. We'll move beyond simple calculations and explore the practical significance of understanding fractions and their decimal equivalents. This understanding is essential for everyday tasks, from cooking and sewing to more complex fields like engineering and finance.
Introduction: Understanding Fractions and Halves
The phrase "half of" inherently involves the concept of fractions. A fraction represents a part of a whole. The simplest fraction, representing one half, is denoted as ½ or 0.5. When we say "half of 2," we're essentially asking for ½ x 2. This is equivalent to dividing 2 by 2. Similarly, "half of 3" is ½ x 3 or 3 ÷ 2, and "half of 8" is ½ x 8 or 8 ÷ 2.
Calculating Half of 2, 3, and 8: A Step-by-Step Approach
Let's tackle each calculation individually, illustrating the process and highlighting the different representation methods:
-
Half of 2:
- Fraction Method: ½ x 2 = 2/2 = 1
- Decimal Method: 0.5 x 2 = 1
- Division Method: 2 ÷ 2 = 1
-
Half of 3:
- Fraction Method: ½ x 3 = 3/2 = 1 ½ (This is an improper fraction, meaning the numerator is larger than the denominator)
- Decimal Method: 0.5 x 3 = 1.5
- Division Method: 3 ÷ 2 = 1.5
-
Half of 8:
- Fraction Method: ½ x 8 = 8/2 = 4
- Decimal Method: 0.5 x 8 = 4
- Division Method: 8 ÷ 2 = 4
Notice that the results for half of 2 and half of 8 are whole numbers, while half of 3 results in a fraction or decimal. This illustrates that dividing an even number by 2 always yields a whole number, while dividing an odd number by 2 results in a fraction or decimal, representing a value between two whole numbers.
Understanding Different Representations: Fractions, Decimals, and Percentages
The examples above showcase three common ways to represent halves:
-
Fractions: Fractions use a numerator (top number) and a denominator (bottom number) to express a part of a whole. ½, ¾, and ⅘ are examples. Fractions provide a precise and unambiguous representation of parts of a whole.
-
Decimals: Decimals use a base-ten system to represent numbers. The decimal point separates the whole number from the fractional part. 0.5, 0.75, and 0.8 are examples. Decimals are often preferred for calculations involving addition, subtraction, multiplication, and division, particularly with the aid of calculators.
-
Percentages: Percentages express a fraction as a portion of 100. Fifty percent (50%) is equivalent to ½, seventy-five percent (75%) is equivalent to ¾, and eighty percent (80%) is equivalent to ⅘. Percentages are useful for representing proportions and comparing quantities. Half of a number can be expressed as 50% of that number.
Beyond the Basics: Extending the Concept of Halves
The concept of finding "half of" extends far beyond simple numbers. Consider these examples:
-
Half of a Quantity: If you have 12 apples, half of them is 6 apples (12 ÷ 2 = 6).
-
Half of a Measurement: If a piece of wood is 10 meters long, half its length is 5 meters (10 ÷ 2 = 5).
-
Half of a Time Period: Half an hour is 30 minutes (60 minutes ÷ 2 = 30 minutes).
-
Half in Geometry: Finding the midpoint of a line segment involves calculating half the distance between its endpoints.
-
Half in Data Analysis: Calculating the median (the middle value) of a dataset often involves finding the middle point, conceptually similar to finding a half.
Practical Applications: Where Finding Halves is Essential
The ability to quickly and accurately calculate halves is crucial across numerous fields:
-
Cooking and Baking: Recipes often require halving or doubling ingredient quantities, necessitating a clear understanding of fractions and their decimal equivalents.
-
Sewing and Tailoring: Accurate measurements and adjustments often involve halving lengths or widths of fabric.
-
Construction and Engineering: Precise measurements and calculations are fundamental to building structures and designing machinery. Halving dimensions is a common task.
-
Finance: Calculating interest, discounts, and profit margins frequently involves working with percentages and fractions, which are directly related to the concept of halves.
-
Everyday Life: Splitting bills, sharing resources, and making fair divisions often require calculating halves.
Explanation of the Mathematical Principles Involved
The core mathematical principle behind finding "half of" a number is division. When we find "half of x," we're essentially dividing x by 2. This is because "half" implies splitting something into two equal parts. The operation can be represented as:
- ½ * x = x ÷ 2
This relationship holds true regardless of whether 'x' is a whole number, a fraction, or a decimal. The result may be a whole number, a fraction, or a decimal, depending on the value of 'x'.
Frequently Asked Questions (FAQ)
-
Q: What if I need to find more than half of a number?
- A: To find a different fraction of a number, you would multiply the number by that fraction. For example, to find ¾ of 12, you would calculate (3/4) * 12 = 9.
-
Q: How can I easily calculate half of a number mentally?
- A: For even numbers, simply divide by 2. For odd numbers, divide by 2 and the result will be a number and a half. Practice with smaller numbers to improve your mental calculation skills.
-
Q: Are there different ways to express "half"?
- A: Yes, "half" can be expressed as ½, 0.5, 50%, or one out of two.
Conclusion: Mastering the Concept of Halves
Understanding the concept of finding "half of" a number is a foundational skill in mathematics with far-reaching practical applications. This article has explored various methods for calculating halves, clarified the use of fractions, decimals, and percentages, and highlighted the importance of this concept across different fields. By mastering this fundamental concept, you equip yourself with a valuable tool for tackling more complex mathematical problems and real-world challenges. The ability to easily work with fractions, decimals, and percentages directly contributes to improved problem-solving abilities and a deeper appreciation for the power of mathematics in our daily lives. Remember, the seemingly simple act of finding "half of" something opens the door to a broader understanding of numerical relationships and their practical applications.
Latest Posts
Latest Posts
-
How Many Bytes In Char
Sep 07, 2025
-
160 Degrees C To Fahrenheit
Sep 07, 2025
-
What Does An Enzyme Do
Sep 07, 2025
-
What Hemisphere Is Georgia In
Sep 07, 2025
-
Born In 83 How Old
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about Half Of 2 3 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.