Hcf Of 24 And 32
cibeltiagestion
Sep 07, 2025 · 7 min read
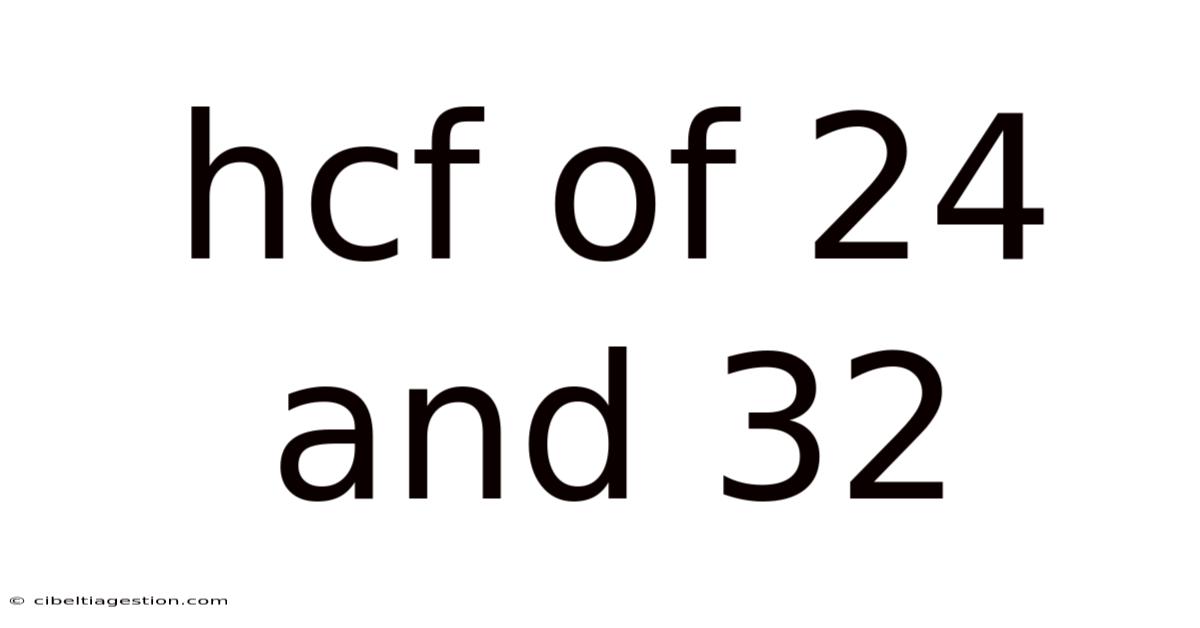
Table of Contents
Understanding the Highest Common Factor (HCF) of 24 and 32: A Deep Dive
Finding the Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), of two numbers is a fundamental concept in mathematics. This article will explore the HCF of 24 and 32 in detail, explaining multiple methods to calculate it and delving into the underlying mathematical principles. We'll cover various techniques, from prime factorization to the Euclidean algorithm, ensuring a comprehensive understanding for learners of all levels. This guide will equip you with the knowledge to confidently tackle similar problems and appreciate the significance of HCF in various mathematical applications.
Introduction: What is the Highest Common Factor?
The Highest Common Factor (HCF) of two or more numbers is the largest number that divides each of them without leaving a remainder. In simpler terms, it's the biggest number that's a factor of both numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The highest number that appears in both lists is 6, so the HCF of 12 and 18 is 6. Understanding HCF is crucial for simplifying fractions, solving algebraic problems, and working with ratios and proportions. This article will specifically focus on finding the HCF of 24 and 32, illustrating several methods to achieve this.
Method 1: Prime Factorization
This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. Let's apply this to find the HCF of 24 and 32.
Step 1: Find the prime factorization of 24.
24 can be broken down as follows:
24 = 2 x 12 = 2 x 2 x 6 = 2 x 2 x 2 x 3 = 2³ x 3
Step 2: Find the prime factorization of 32.
32 can be broken down as follows:
32 = 2 x 16 = 2 x 2 x 8 = 2 x 2 x 2 x 4 = 2 x 2 x 2 x 2 x 2 = 2⁵
Step 3: Identify common prime factors.
Both 24 and 32 share the prime factor 2.
Step 4: Determine the lowest power of the common prime factors.
The lowest power of 2 present in both factorizations is 2³.
Step 5: Calculate the HCF.
The HCF is the product of the common prime factors raised to their lowest power. In this case, it's 2³.
Therefore, the HCF of 24 and 32 is 2³ = 8.
Method 2: Listing Factors
This is a more straightforward method, particularly useful for smaller numbers.
Step 1: List all the factors of 24.
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Step 2: List all the factors of 32.
Factors of 32: 1, 2, 4, 8, 16, 32
Step 3: Identify common factors.
The common factors of 24 and 32 are 1, 2, 4, and 8.
Step 4: Determine the highest common factor.
The highest number among the common factors is 8.
Therefore, the HCF of 24 and 32 is 8.
Method 3: The Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the HCF of two numbers, particularly useful for larger numbers where prime factorization can become cumbersome. It's based on the principle that the HCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Step 1: Divide the larger number (32) by the smaller number (24).
32 ÷ 24 = 1 with a remainder of 8.
Step 2: Replace the larger number with the remainder.
The new pair of numbers is 24 and 8.
Step 3: Repeat the process.
24 ÷ 8 = 3 with a remainder of 0.
Step 4: The HCF is the last non-zero remainder.
Since the remainder is 0, the HCF is the previous remainder, which is 8.
Therefore, the HCF of 24 and 32 is 8.
A Deeper Look at the Mathematics Behind HCF
The concept of HCF is deeply rooted in number theory. It's intimately connected to the idea of divisibility and prime factorization. Every positive integer can be uniquely represented as a product of prime numbers (Fundamental Theorem of Arithmetic). When we find the prime factorization of two numbers, we are essentially breaking them down into their fundamental building blocks. The HCF represents the shared building blocks, raised to the lowest power they appear in either number. This is why the prime factorization method works so effectively.
The Euclidean algorithm, on the other hand, provides an elegant and efficient alternative. Its effectiveness stems from the property that the HCF of two numbers remains unchanged when the larger number is replaced by its difference with the smaller number. This iterative process quickly reduces the numbers until the HCF is revealed as the last non-zero remainder. This method avoids the need for explicit prime factorization, making it particularly advantageous for larger numbers.
Applications of HCF
The HCF has numerous applications across various branches of mathematics and beyond:
-
Simplifying Fractions: Finding the HCF of the numerator and denominator allows you to simplify a fraction to its lowest terms. For example, the fraction 24/32 can be simplified to 3/4 by dividing both numerator and denominator by their HCF (8).
-
Solving Algebraic Problems: HCF is used in solving algebraic equations and simplifying expressions involving fractions and ratios.
-
Ratio and Proportion Problems: HCF helps in simplifying ratios and finding equivalent ratios.
-
Measurement and Geometry: HCF is used in finding the largest possible square tile to cover a rectangular area without any gaps or overlaps.
-
Cryptography: Concepts related to HCF, such as the Euclidean algorithm, play a significant role in modern cryptography, particularly in public-key cryptography systems.
-
Computer Science: HCF computations are used in various algorithms and data structures.
Frequently Asked Questions (FAQ)
-
Q: What if the HCF of two numbers is 1?
A: If the HCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they share no common factors other than 1.
-
Q: Can the HCF of two numbers be larger than either number?
A: No. The HCF is always less than or equal to the smaller of the two numbers.
-
Q: How do I find the HCF of more than two numbers?
A: You can extend any of the methods described above. For example, using prime factorization, you would find the prime factorization of each number and then identify the common prime factors raised to their lowest power. The Euclidean algorithm can also be extended to handle multiple numbers by iteratively finding the HCF of pairs of numbers.
-
Q: What's the difference between HCF and LCM?
A: HCF (Highest Common Factor) is the largest number that divides both numbers without a remainder, while LCM (Least Common Multiple) is the smallest number that is a multiple of both numbers. They are inversely related; for two numbers a and b, HCF(a, b) * LCM(a, b) = a * b
Conclusion
Finding the HCF of 24 and 32, as demonstrated through prime factorization, listing factors, and the Euclidean algorithm, highlights the fundamental importance of this concept in mathematics. Understanding the HCF is not merely an academic exercise; it's a crucial tool with wide-ranging applications in diverse fields. Whether you are simplifying fractions, solving complex equations, or delving into the intricacies of number theory, the ability to efficiently calculate the HCF will prove invaluable. By mastering these methods, you will develop a deeper appreciation for the elegant structure and interconnectedness of mathematical concepts. Remember to choose the method best suited to the numbers involved – prime factorization is often intuitive for smaller numbers, while the Euclidean algorithm shines with larger ones. Regardless of the method chosen, the result remains consistent: the HCF of 24 and 32 is 8.
Latest Posts
Latest Posts
-
Where Does Glycolysis Take Place
Sep 07, 2025
-
What Percentage Is A Quorum
Sep 07, 2025
-
Coati Vs Fig Eating Bat
Sep 07, 2025
-
85 Cm How Many Inches
Sep 07, 2025
-
Molar Mass Of Magnesium Hydroxide
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 24 And 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.