How Many 1/4 In 3/4
cibeltiagestion
Sep 10, 2025 · 6 min read
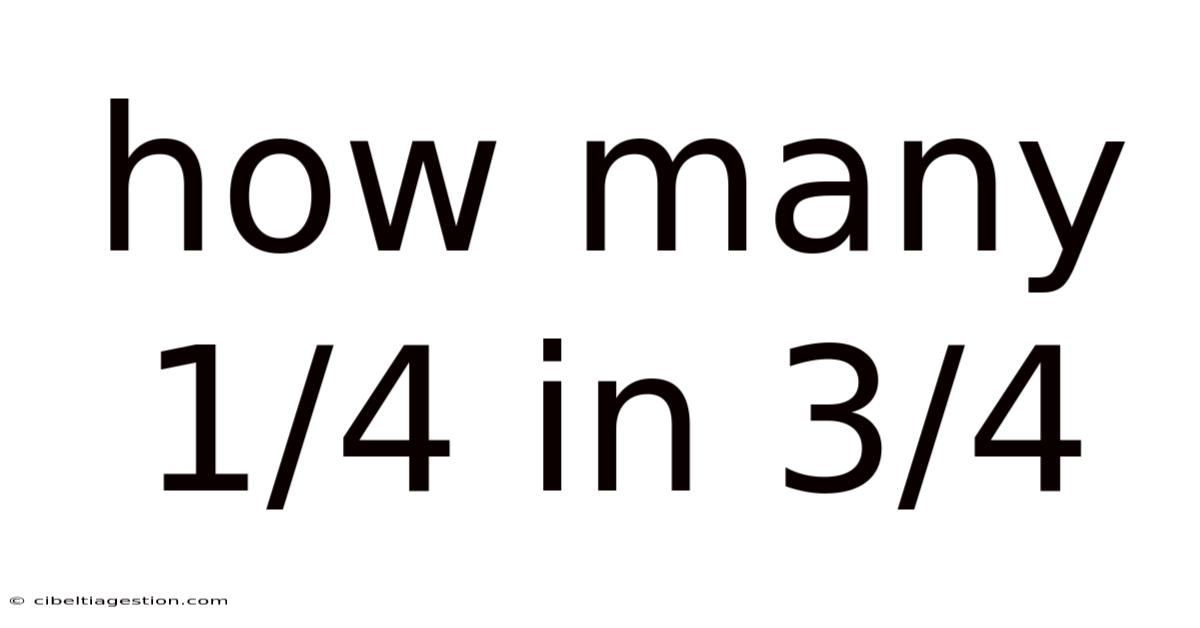
Table of Contents
How Many 1/4s are in 3/4? Understanding Fractions and Division
This seemingly simple question, "How many 1/4s are in 3/4?", opens the door to a deeper understanding of fractions, division, and the fundamental principles of mathematics. It's a question that might seem trivial at first glance, but mastering the concepts involved is crucial for tackling more complex mathematical problems later on. This article will not only answer the question directly but will also explore the underlying concepts, providing you with a solid foundation in fractional arithmetic.
Introduction: A Foundation in Fractions
Before we dive into the specific problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), like this: a/b. The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
In our question, we're dealing with quarters (1/4). A quarter represents one out of four equal parts of a whole. Think of a pizza cut into four slices – each slice is 1/4 of the pizza. The question asks how many of these 1/4 slices are present in 3/4 of the pizza.
The Simple Solution: Direct Calculation
The most straightforward way to solve "How many 1/4s are in 3/4?" is through direct division. We can think of this as: (3/4) ÷ (1/4).
Remember that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply flipping the numerator and denominator. The reciprocal of 1/4 is 4/1, or simply 4.
Therefore, our calculation becomes: (3/4) x (4/1). Multiplying the numerators together (3 x 4 = 12) and the denominators together (4 x 1 = 4), we get 12/4. Simplifying this fraction by dividing both numerator and denominator by 4, we arrive at the answer: 3.
Therefore, there are 3 one-fourths (1/4) in three-fourths (3/4).
Visualizing the Solution: A Practical Approach
Understanding fractions can be greatly enhanced by visualizing them. Imagine a pie cut into four equal slices. Each slice represents 1/4 of the pie. If you have three of these slices, you have 3/4 of the pie. Counting the slices directly shows you that there are three 1/4 slices in 3/4 of the pie. This visual representation reinforces the mathematical solution.
Expanding the Concept: Working with Different Fractions
The method we used above applies to other fractions as well. Let's consider a slightly more challenging example: How many 1/8s are in 3/4?
-
Find a Common Denominator: To compare these fractions, we need a common denominator. The least common multiple of 4 and 8 is 8.
-
Convert to Equivalent Fractions: We convert 3/4 to an equivalent fraction with a denominator of 8. To do this, we multiply both the numerator and the denominator by 2: (3 x 2)/(4 x 2) = 6/8.
-
Perform the Division: Now we have 6/8 ÷ 1/8. This is equivalent to (6/8) x (8/1) = 48/8 = 6.
Therefore, there are 6 one-eighths (1/8) in three-fourths (3/4).
This example demonstrates how finding a common denominator is crucial when working with fractions that don't have the same denominator. This process allows for a direct comparison and simplifies the calculation.
The Importance of Understanding the Underlying Principles
The seemingly simple question "How many 1/4s are in 3/4?" is more than just a calculation. It provides a foundational understanding of several key mathematical principles:
-
Fraction Equivalence: Understanding that 3/4 is equivalent to 6/8, 9/12, and so on, is crucial for solving many fractional problems.
-
Division of Fractions: Mastering the method of dividing by a fraction (multiplying by its reciprocal) is a cornerstone of fractional arithmetic.
-
Least Common Multiple (LCM): Finding the LCM of denominators is essential for adding, subtracting, and comparing fractions.
-
Greatest Common Divisor (GCD): The GCD helps in simplifying fractions to their lowest terms.
These principles are not limited to simple fraction problems. They are building blocks for more complex mathematical concepts encountered in algebra, calculus, and other advanced mathematical fields.
Real-World Applications: Where Fractions Matter
Fractions are not just abstract mathematical concepts; they are essential tools used in various real-world situations:
-
Cooking and Baking: Recipes often require fractional measurements of ingredients. Understanding fractions is vital for accurate measurements and successful baking.
-
Construction and Engineering: Precise measurements and calculations involving fractions are essential in construction and engineering projects to ensure accuracy and safety.
-
Finance and Accounting: Fractions are used extensively in financial calculations, such as calculating interest rates, discounts, and profit margins.
-
Data Analysis: In data analysis and statistics, fractions are used to represent proportions and percentages.
Mastering fractions is not just about passing a math test; it's about developing essential skills applicable to numerous aspects of daily life and various professional fields.
Beyond the Basics: Exploring More Complex Scenarios
Let's consider some slightly more advanced variations of the initial question:
Scenario 1: How many 2/4s are in 3/4?
This problem is solved similarly to the initial one, except now we're dividing 3/4 by 2/4:
(3/4) ÷ (2/4) = (3/4) x (4/2) = 12/8 = 3/2 = 1.5
There are 1.5 two-fourths in three-fourths.
Scenario 2: How many 1/3s are in 3/4?
Here, we need to find a common denominator:
-
Convert fractions to equivalent fractions with a common denominator (12): 3/4 becomes 9/12 and 1/3 becomes 4/12
-
Divide: (9/12) ÷ (4/12) = (9/12) x (12/4) = 108/48 = 9/4 = 2.25
There are 2.25 one-thirds in three-fourths.
These scenarios highlight the importance of adaptability in applying the fundamental principles of fraction manipulation to different problem types.
Frequently Asked Questions (FAQ)
-
Q: What if the denominator is larger than the numerator? A: If you're dividing a smaller fraction by a larger fraction, your answer will be a fraction less than 1.
-
Q: Can I use a calculator for these problems? A: Yes, many calculators have fraction functions that can simplify these calculations. However, understanding the underlying principles is still crucial for problem-solving.
-
Q: Why is it important to learn fractions? A: Fractions are fundamental to higher-level mathematics and are used extensively in various fields. A strong understanding of fractions is essential for success in many areas of life.
-
Q: How can I practice more fraction problems? A: Work through textbooks, online resources, and practice worksheets. Focus on understanding the principles and applying them to different scenarios.
Conclusion: Mastering Fractions – A Stepping Stone to Success
The seemingly simple question, "How many 1/4s are in 3/4?", serves as a powerful introduction to the world of fractions. Mastering the concepts discussed here—fraction equivalence, division of fractions, and finding common denominators—provides a solid foundation for tackling more advanced mathematical problems. These skills are not just confined to the classroom; they are invaluable tools in everyday life and in various professions. By understanding and applying these principles, you build a stronger foundation for future mathematical endeavors and enhance your problem-solving abilities across numerous disciplines. Remember, consistent practice and a focus on understanding the underlying concepts are key to mastering fractions and achieving mathematical fluency.
Latest Posts
Latest Posts
-
Is 0 625 Rational Or Irrational
Sep 10, 2025
-
What Colors To Make Orange
Sep 10, 2025
-
In General Critical Thinking Means
Sep 10, 2025
-
What Does Thug Life Mean
Sep 10, 2025
-
Rural Areas Have Of Development
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about How Many 1/4 In 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.