Is 2/3 More Than 1/2
cibeltiagestion
Sep 02, 2025 · 5 min read
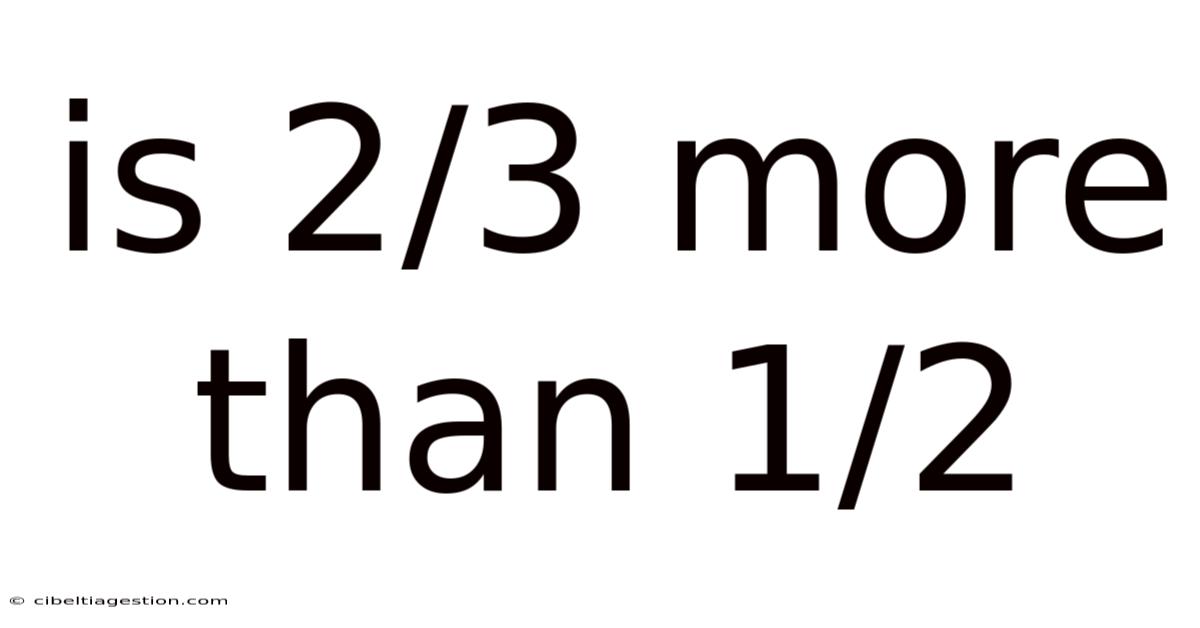
Table of Contents
Is 2/3 More Than 1/2? A Deep Dive into Fraction Comparison
This article explores the seemingly simple question: is 2/3 more than 1/2? While the answer might seem obvious to some, understanding why 2/3 is greater than 1/2 requires a deeper understanding of fractions and their representation. We'll delve into various methods for comparing fractions, providing a comprehensive explanation suitable for learners of all levels. This will include visual representations, numerical comparisons, and even a touch of algebraic reasoning. By the end, you'll not only know the answer but also possess the tools to confidently compare any two fractions.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's briefly review what fractions represent. A fraction, such as 2/3, consists of two parts:
- Numerator: The top number (2 in this case) indicates how many parts we have.
- Denominator: The bottom number (3 in this case) indicates the total number of equal parts the whole is divided into.
So, 2/3 means we have 2 parts out of a total of 3 equal parts. Similarly, 1/2 means we have 1 part out of a total of 2 equal parts.
Method 1: Visual Comparison using Fraction Circles
A powerful way to compare fractions is through visual representation. Imagine two circles, each representing a whole.
- Circle 1: Divide this circle into three equal parts. Shade two of these parts to represent 2/3.
- Circle 2: Divide this circle into two equal parts. Shade one of these parts to represent 1/2.
By visually comparing the shaded areas of both circles, it becomes clear that the shaded area representing 2/3 is larger than the shaded area representing 1/2. This visual demonstration provides an intuitive understanding of why 2/3 > 1/2.
Method 2: Finding a Common Denominator
A more numerical approach involves finding a common denominator. This is a number that is a multiple of both denominators (3 and 2). The least common multiple of 3 and 2 is 6.
- Converting 2/3: To convert 2/3 to a fraction with a denominator of 6, we multiply both the numerator and the denominator by 2: (2 x 2) / (3 x 2) = 4/6.
- Converting 1/2: To convert 1/2 to a fraction with a denominator of 6, we multiply both the numerator and the denominator by 3: (1 x 3) / (2 x 3) = 3/6.
Now that both fractions have the same denominator, we can easily compare their numerators. Since 4 > 3, it follows that 4/6 > 3/6, therefore 2/3 > 1/2. This method provides a robust and reliable way to compare fractions, regardless of their complexity.
Method 3: Decimal Conversion
Another approach is to convert both fractions into decimals. This involves dividing the numerator by the denominator for each fraction.
- 2/3: 2 ÷ 3 ≈ 0.6667
- 1/2: 1 ÷ 2 = 0.5
Comparing the decimal values, 0.6667 > 0.5, confirming that 2/3 is greater than 1/2. This method is particularly useful when dealing with fractions that are difficult to visualize or find a common denominator for easily.
Method 4: Cross-Multiplication
Cross-multiplication offers a quick method for comparing fractions. Multiply the numerator of the first fraction by the denominator of the second fraction, and vice-versa.
- 2/3 and 1/2:
- 2 (numerator of 2/3) x 2 (denominator of 1/2) = 4
- 3 (denominator of 2/3) x 1 (numerator of 1/2) = 3
Since 4 > 3, we conclude that 2/3 > 1/2. This method provides a concise and efficient way to compare fractions, especially when dealing with larger numbers.
Method 5: Understanding the Magnitude of the Fractions
Beyond the mathematical methods, consider the inherent values. One-half represents exactly half of a whole. Two-thirds represents more than half, as it is two parts out of three equal parts. This intuitive understanding reinforces the fact that 2/3 is inherently larger than 1/2.
The Importance of Understanding Fraction Comparison
The ability to compare fractions is a fundamental skill in mathematics, extending beyond simple arithmetic. It's crucial for:
- Problem-solving: Many real-world problems, from measuring ingredients in cooking to calculating proportions in construction, require accurate fraction comparison.
- Data analysis: Understanding fractions is essential for interpreting data presented in fractional form, common in various fields like finance and statistics.
- Higher-level mathematics: Proficiency in fraction comparison forms the basis for understanding more advanced mathematical concepts, such as algebra and calculus.
Frequently Asked Questions (FAQ)
Q1: Are there any situations where 1/2 could be considered "larger" than 2/3?
A1: No, in the context of numerical value, 2/3 will always be greater than 1/2. However, the context might sometimes alter the interpretation. For example, if we are dealing with negative fractions, then -1/2 would be greater than -2/3.
Q2: How can I teach fraction comparison to children?
A2: Visual aids like fraction circles, bars, or even real-world objects (like pizza slices) are very effective. Start with simple comparisons and gradually introduce more complex fractions. Games and interactive activities can also make learning fun and engaging.
Q3: What if I have more than two fractions to compare?
A3: The same methods apply, but you might find it easier to convert all fractions to decimals or find a common denominator for all before comparing. For example if you're comparing 1/2, 2/3, and 5/8 you'd convert them to a common denominator of 24 giving you 12/24, 16/24, and 15/24, so clearly 2/3 is the largest.
Conclusion
In conclusion, yes, 2/3 is more than 1/2. We have explored multiple methods – visual comparisons, common denominators, decimal conversions, cross-multiplication, and intuitive understanding – to demonstrate this fact conclusively. Understanding fraction comparison is a crucial skill, essential not just for academic success but also for navigating numerous real-world situations. By mastering these methods, you'll develop a strong foundation in mathematics and improve your problem-solving abilities. Remember to practice regularly to solidify your understanding and build confidence in tackling more complex fraction problems.
Latest Posts
Latest Posts
-
How Many Cups Is 12oz
Sep 02, 2025
-
Main Properties Of Musical Sounds
Sep 02, 2025
-
Which Hormone Promotes Protein Catabolism
Sep 02, 2025
-
1 Ounce To 1 Pound
Sep 02, 2025
-
1 5 Repeating As A Fraction
Sep 02, 2025
Related Post
Thank you for visiting our website which covers about Is 2/3 More Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.