Is 5/6 Greater Than 1/2
cibeltiagestion
Sep 12, 2025 · 5 min read
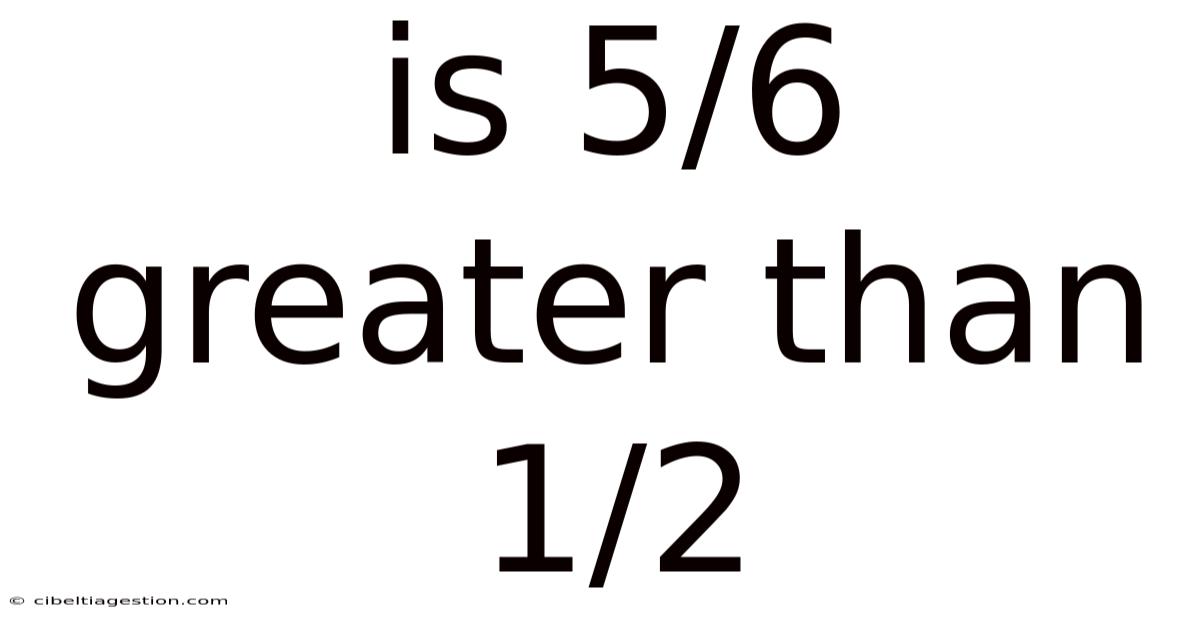
Table of Contents
Is 5/6 Greater Than 1/2? A Deep Dive into Fraction Comparison
Are you struggling with comparing fractions? Understanding whether 5/6 is greater than 1/2 might seem simple at first glance, but it's a fundamental concept in mathematics with broader implications for understanding ratios, proportions, and even more advanced concepts. This article will not only answer the question definitively but will also equip you with the tools and knowledge to confidently compare any two fractions. We'll explore multiple methods, delve into the underlying mathematical principles, and even address some frequently asked questions.
Introduction: Understanding Fractions
Before we tackle the specific comparison of 5/6 and 1/2, let's briefly review what fractions represent. A fraction, like 5/6, represents a part of a whole. The number on the top, the numerator, indicates how many parts we have. The number on the bottom, the denominator, indicates how many equal parts the whole is divided into. So, 5/6 means we have 5 out of 6 equal parts of a whole.
Similarly, 1/2 means we have 1 out of 2 equal parts of a whole. Understanding this basic representation is crucial for comparing fractions.
Method 1: Visual Comparison
One of the easiest ways to compare fractions, especially for beginners, is through visual representation. Imagine two identical pizzas.
- Pizza 1: Cut into 6 equal slices. You eat 5 of them (5/6).
- Pizza 2: Cut into 2 equal slices. You eat 1 of them (1/2).
Which pizza did you eat more of? Visually, it's clear that you ate a significantly larger portion of Pizza 1 (5/6) than Pizza 2 (1/2). This visual method helps build intuition and understanding before moving to more abstract methods.
Method 2: Finding a Common Denominator
This is a more formal and widely applicable method. The key idea is to rewrite both fractions so they have the same denominator. This allows for direct comparison of the numerators.
To find a common denominator for 5/6 and 1/2, we need to find a number that is divisible by both 6 and 2. The least common multiple (LCM) of 6 and 2 is 6.
- 5/6 already has a denominator of 6.
- 1/2 needs to be rewritten with a denominator of 6. To do this, we multiply both the numerator and the denominator by 3 (because 2 x 3 = 6): 1/2 = (1 x 3) / (2 x 3) = 3/6
Now we can compare: 5/6 and 3/6. Since 5 > 3, we can conclude that 5/6 > 1/2.
Method 3: Converting to Decimals
Another effective approach is to convert both fractions into decimals. This method is particularly useful when dealing with more complex fractions or when you need a numerical representation for further calculations.
- 5/6: To convert 5/6 to a decimal, divide 5 by 6: 5 ÷ 6 ≈ 0.833
- 1/2: To convert 1/2 to a decimal, divide 1 by 2: 1 ÷ 2 = 0.5
Since 0.833 > 0.5, we again conclude that 5/6 > 1/2.
Method 4: Comparing to a Benchmark Fraction (1/2)
This method is excellent for quick estimations. We can use 1/2 as a benchmark to compare other fractions. If a fraction is greater than 1/2, its numerator will be more than half its denominator. If it's less than 1/2, its numerator will be less than half its denominator.
In the case of 5/6, half of the denominator (6) is 3. Since the numerator (5) is greater than 3, we know that 5/6 is greater than 1/2.
The Mathematical Reasoning Behind Fraction Comparison
The methods described above all stem from the fundamental principles of fractions and equivalent fractions. Equivalent fractions are fractions that represent the same value, even though they look different. For instance, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions. Finding a common denominator is essentially finding equivalent fractions for both fractions so that we can compare them directly.
The conversion to decimals relies on the fact that fractions represent division. Dividing the numerator by the denominator gives us the decimal equivalent. Comparing the decimal equivalents is a straightforward numerical comparison.
Beyond the Basics: Extending Fraction Comparison Skills
Understanding how to compare 5/6 and 1/2 is a stepping stone to more advanced concepts. These skills are essential for:
- Solving algebraic equations: Many algebraic equations involve fractions, and comparing fractions is crucial for solving them.
- Understanding ratios and proportions: Ratios and proportions are expressed using fractions, and the ability to compare fractions directly translates to understanding these concepts.
- Data analysis: In statistical analysis and data representation, fractions are commonly used. Comparing fractions allows for meaningful interpretation of data.
- Geometry and measurement: Many geometric calculations involve fractions and ratios, requiring the skills discussed in this article.
Frequently Asked Questions (FAQ)
Q1: Are there any other ways to compare fractions besides the ones mentioned?
A1: Yes, there are. One method involves cross-multiplication. To compare a/b and c/d, you can cross-multiply: a x d and b x c. If a x d > b x c, then a/b > c/d.
Q2: What if the fractions have different denominators and finding a common denominator is difficult?
A2: While finding a common denominator is always possible, it can sometimes be computationally intensive. In such cases, converting to decimals is often a more practical approach.
Q3: Is there a trick to quickly estimate whether a fraction is greater or less than 1/2?
A3: Yes. As mentioned earlier, if the numerator is more than half the denominator, the fraction is greater than 1/2. If the numerator is less than half the denominator, the fraction is less than 1/2.
Conclusion: Mastering Fraction Comparison
Comparing fractions, even seemingly simple ones like 5/6 and 1/2, is a crucial skill in mathematics. This article provided several methods – visual comparison, finding a common denominator, converting to decimals, and using benchmarks – to determine that 5/6 is indeed greater than 1/2. However, the real takeaway is not just the answer to this specific comparison, but the development of a deeper understanding of fractions and the ability to confidently compare any two fractions you encounter. Remember to practice these methods regularly to build your fluency and confidence in working with fractions. The more you practice, the easier and more intuitive these comparisons will become. Mastering this fundamental skill opens doors to a wider world of mathematical understanding and problem-solving.
Latest Posts
Latest Posts
-
Use Cacophonous In A Sentence
Sep 12, 2025
-
Referenceerror Textencoder Is Not Defined
Sep 12, 2025
-
What Is 200ml In Oz
Sep 12, 2025
-
Is Philosophy A Social Science
Sep 12, 2025
-
How Much Is 1 6 K
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Is 5/6 Greater Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.