Percent Of 4 Is 7
cibeltiagestion
Sep 08, 2025 · 5 min read
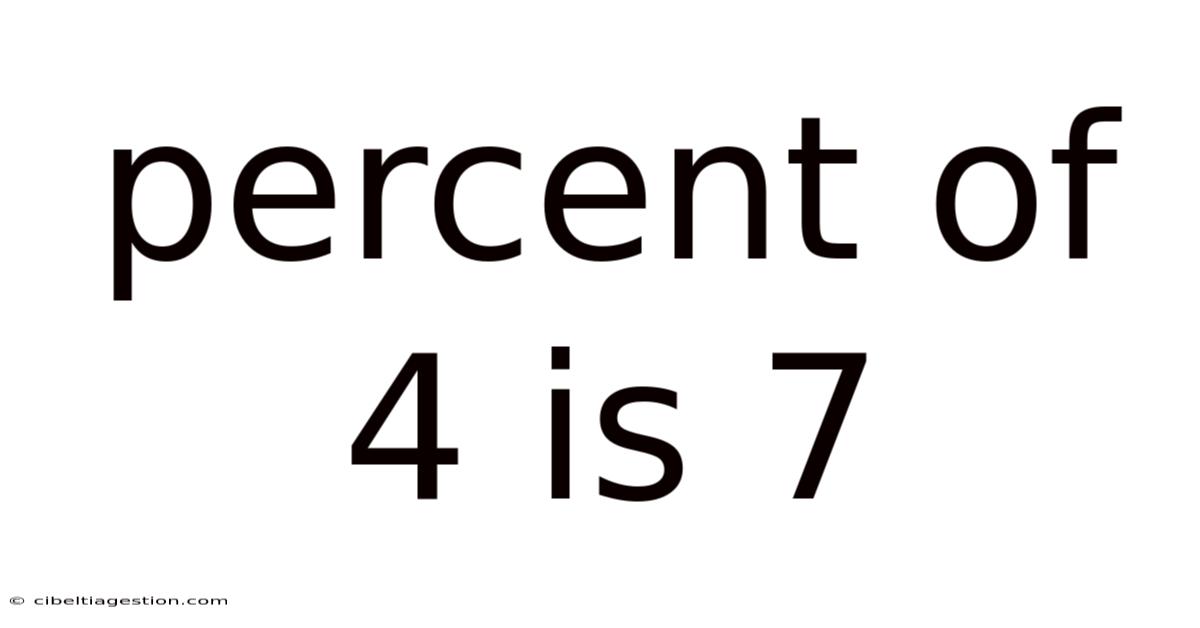
Table of Contents
Decoding the Paradox: Understanding "Percent of 4 is 7"
The statement "percent of 4 is 7" presents a seemingly paradoxical situation. It implies a percentage that, when applied to the number 4, results in 7. This is counterintuitive because percentages are typically understood as representing a portion of a whole, and a portion cannot be larger than the whole. However, this seemingly impossible problem unveils a fascinating exploration of mathematical concepts, particularly the power of algebra and its ability to resolve seemingly impossible scenarios. This article will delve into the solution, explaining the underlying mathematical principles and exploring various approaches to solving this type of problem. We'll also address common misconceptions and provide a solid foundation for understanding percentage calculations.
Understanding Percentages: A Foundation
Before tackling the core problem, let's solidify our understanding of percentages. A percentage is a way of expressing a fraction or ratio as a number out of 100. For example, 50% means 50 out of 100, which simplifies to 1/2 or 0.5. The key is that percentages represent parts of a whole. This is crucial because the problem "percent of 4 is 7" initially seems to violate this fundamental principle.
The standard formula for calculating percentages is:
(Percentage/100) * Whole = Part
Where:
- Percentage is the percentage rate.
- Whole is the total value.
- Part is the portion of the whole.
This formula is the backbone of many percentage-related calculations, and we'll use variations of it to solve our core problem.
Solving "Percent of 4 is 7": The Algebraic Approach
The statement "percent of 4 is 7" can be translated into an algebraic equation. Let's represent the unknown percentage as 'x'. The equation becomes:
(x/100) * 4 = 7
Now, we can solve for 'x' using algebraic manipulation:
-
Multiply both sides by 100: 4x = 700
-
Divide both sides by 4: x = 175
Therefore, the solution is 175%. This result might initially seem surprising, but it's perfectly valid within the framework of mathematics. 175% signifies a value exceeding the original whole (100%). In this case, 175% of 4 equates to 7.
Graphical Representation and Intuitive Understanding
While the algebraic approach provides the precise solution, a graphical representation can aid in intuitive understanding. Imagine a bar representing the number 4. To represent 100% of 4, the bar is divided into four equal segments, each representing 1. To achieve 7, we need more than one whole bar of 4. In fact, we need almost two full bars. This visual representation highlights that the percentage must exceed 100%.
We can further break down the calculation:
- 100% of 4 = 4
- To reach 7, we need an additional 3 (7 - 4 = 3).
- The additional 3 represents a percentage of 4.
- (3/4) * 100% = 75%
Adding this 75% to the initial 100%, we arrive at the total percentage: 100% + 75% = 175%.
Exploring Different Approaches: Proportions
We can also approach this problem using the concept of proportions. We can set up a proportion to represent the relationship:
- x/100 = 7/4
This proportion states that the unknown percentage (x) is to 100 as 7 is to 4. Cross-multiplying gives us:
4x = 700
Dividing by 4 again yields x = 175. This method reinforces the previous solution and showcases the versatility of proportional reasoning in solving percentage problems.
Addressing Common Misconceptions and Errors
Many students initially struggle with problems like "percent of 4 is 7" because they're accustomed to percentages being less than or equal to 100%. This misconception stems from frequently encountering percentages representing parts of a whole, where the percentage cannot exceed 100%. However, it's essential to remember that percentages can represent values greater than 100%, signifying an increase beyond the initial whole. The key is to correctly translate the word problem into a mathematical equation. Many errors arise from incorrect equation formulation.
Expanding the Concept: Applications and Real-World Examples
Understanding percentages exceeding 100% is vital in various real-world contexts. For example:
- Percentage Increase/Decrease: Calculating percentage changes (e.g., population growth, stock market fluctuations) often involves percentages above 100% when dealing with significant increases.
- Financial Calculations: Interest rates, returns on investments, and inflation calculations frequently use percentages exceeding 100% to represent substantial growth.
- Data Analysis and Statistics: In various statistical analyses, values exceeding 100% might represent ratios or comparisons where one value significantly surpasses another.
Frequently Asked Questions (FAQ)
Q1: Can a percentage ever be greater than 100%?
A1: Yes, absolutely. A percentage greater than 100% indicates a value exceeding the initial whole or base value.
Q2: Why is this problem considered paradoxical?
A2: The seeming paradox arises from the ingrained notion that a percentage represents a part of a whole, inherently implying a value less than or equal to 100%. However, the mathematical framework allows for percentages greater than 100%, representing growth or increases beyond the initial value.
Q3: What are some common mistakes when solving percentage problems?
A3: Common mistakes include incorrect equation setup, misinterpreting the word problem, and assuming percentages cannot exceed 100%. Careful attention to detail and a thorough understanding of the underlying principles are crucial for accurate calculations.
Q4: How can I improve my understanding of percentages?
A4: Practice solving various types of percentage problems, focusing on translating word problems into mathematical equations. Using visual aids and different solution methods can enhance understanding and build confidence.
Conclusion: Beyond the Paradox
The problem "percent of 4 is 7" initially appears paradoxical because it challenges our typical understanding of percentages. However, by applying algebraic methods, proportional reasoning, and a deeper understanding of percentage concepts, we can effectively solve this type of problem. The solution, 175%, highlights that percentages can indeed exceed 100%, representing values greater than the initial whole. This understanding is critical for solving various real-world problems involving percentage increases, financial calculations, and data analysis. Mastering the concept of percentages, including those exceeding 100%, equips you with a powerful tool for tackling mathematical challenges and making sense of quantitative information in various contexts. Remember that the key lies in accurately translating the word problem into a solvable equation and recognizing that percentages are not limited to values below 100%.
Latest Posts
Latest Posts
-
Speed Of Sound In Fps
Sep 09, 2025
-
What Is 20 Of 64
Sep 09, 2025
-
How Many Ml In 16oz
Sep 09, 2025
-
What Is 50 Years Called
Sep 09, 2025
-
The Provirus State Exists When
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Percent Of 4 Is 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.