Simplify 1 2x 1 2
cibeltiagestion
Sep 15, 2025 · 5 min read
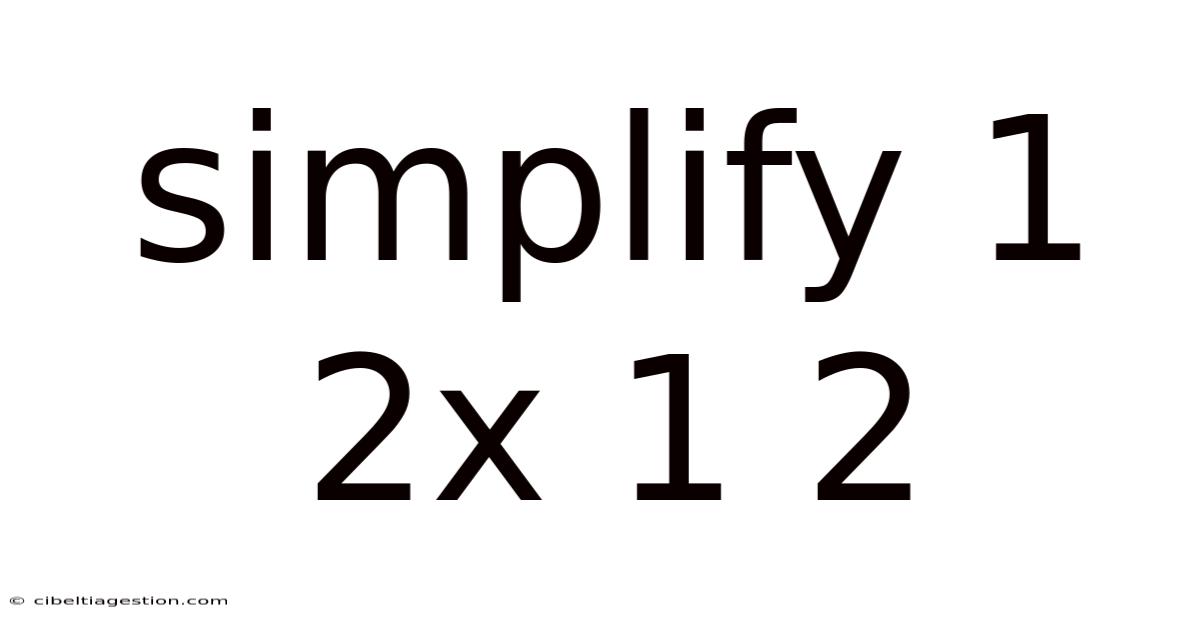
Table of Contents
Simplifying 1 + 2x + 1 + 2: A Comprehensive Guide
This article provides a detailed explanation of how to simplify the algebraic expression 1 + 2x + 1 + 2. We will cover the fundamental principles of algebra involved, walk through the simplification process step-by-step, and address frequently asked questions. Understanding this seemingly simple problem lays the groundwork for tackling more complex algebraic equations. This guide is perfect for students learning basic algebra, as well as anyone looking to refresh their understanding of algebraic simplification.
Introduction: Understanding Algebraic Expressions
Before we dive into simplifying the expression, let's establish a foundational understanding of what algebraic expressions are. An algebraic expression is a mathematical phrase that combines numbers, variables (like x), and operators (+, -, ×, ÷). The goal of simplifying an algebraic expression is to rewrite it in its most concise and equivalent form, without changing its value. This often involves combining like terms. Like terms are terms that have the same variable raised to the same power. For example, 3x and 5x are like terms, but 3x and 3x² are not.
Step-by-Step Simplification of 1 + 2x + 1 + 2
Now, let's tackle the simplification of our expression: 1 + 2x + 1 + 2.
Step 1: Identify Like Terms
First, we identify the like terms in the expression. In this case, we have:
- Constant terms: 1, 1, and 2 (these are numbers without any variables)
- Variable term: 2x (this term contains the variable x)
Step 2: Combine Like Terms
Next, we combine the like terms by adding or subtracting them. Let's start with the constant terms:
1 + 1 + 2 = 4
Now, let's consider the variable term. Since there's only one variable term (2x), it remains unchanged.
Step 3: Write the Simplified Expression
Finally, we combine the simplified constant term and the variable term to obtain the simplified expression:
4 + 2x
Therefore, the simplified form of 1 + 2x + 1 + 2 is 4 + 2x.
Further Explanation: The Commutative and Associative Properties
The simplification process we followed relies on two fundamental properties of arithmetic: the commutative and associative properties.
-
Commutative Property: This property states that the order of addition or multiplication does not affect the result. For example, a + b = b + a, and a × b = b × a. This allows us to rearrange the terms in our expression without changing its value.
-
Associative Property: This property states that the grouping of numbers in addition or multiplication does not affect the result. For example, (a + b) + c = a + (b + c), and (a × b) × c = a × (b × c). This allows us to group like terms together before combining them.
In our example, we implicitly used both properties. We rearranged the terms (commutative property) to group the constants together and then added them (associative property).
Expanding the Concept: More Complex Expressions
While our initial expression was relatively straightforward, the same principles apply to more complex algebraic expressions. Let's consider a slightly more challenging example:
3x² + 5x + 2 + x² - 3x + 1
Step 1: Identify Like Terms:
- x² terms: 3x², x²
- x terms: 5x, -3x
- Constant terms: 2, 1
Step 2: Combine Like Terms:
- x² terms: 3x² + x² = 4x²
- x terms: 5x + (-3x) = 2x
- Constant terms: 2 + 1 = 3
Step 3: Write the Simplified Expression:
The simplified expression is: 4x² + 2x + 3
Dealing with Subtraction: A Note on Negative Signs
When dealing with subtraction in algebraic expressions, remember that subtracting a number is equivalent to adding its negative. For example:
5x - 2x is the same as 5x + (-2x) = 3x
Similarly, 7 - 3x is the same as 7 + (-3x)
Illustrative Examples: Putting it all Together
Let's work through a few more examples to solidify our understanding:
-
Example 1: 2y + 4 + y - 1
- Like terms: 2y, y; 4, -1
- Simplified: 3y + 3
-
Example 2: 5a² - 2a + 3a² + a - 1
- Like terms: 5a², 3a²; -2a, a; -1
- Simplified: 8a² - a - 1
-
Example 3: 4b + 6 - 2b + 3
- Like terms: 4b, -2b; 6, 3
- Simplified: 2b + 9
Frequently Asked Questions (FAQ)
Q1: What happens if there are more than one variable?
A1: You still follow the same process. Combine like terms that have the same variable raised to the same power. For instance, in the expression 3x + 2y + 5x - y, you would combine 3x and 5x to get 8x, and 2y and -y to get y, resulting in a simplified expression of 8x + y.
Q2: What if there are brackets (parentheses)?
A2: If there are brackets, you need to simplify the expressions within the brackets first, before combining like terms. For example, in the expression 2(x + 1) + 3x, you would first expand the brackets to get 2x + 2 + 3x, then combine like terms to get 5x + 2.
Q3: Can I simplify expressions with exponents higher than 2?
A3: Yes, absolutely! The principles remain the same. Combine like terms that have the same variable raised to the same power. For instance, in the expression 4x³ + 2x² + x³ - x, you would combine 4x³ and x³ to get 5x³, leaving the 2x² and -x unchanged, resulting in a simplified expression of 5x³ + 2x² - x.
Q4: What if I make a mistake?
A4: Don't worry! Mistakes are a natural part of the learning process. Carefully review your steps, double-check your calculations, and try again. If you're still stuck, break down the problem into smaller, more manageable parts.
Conclusion: Mastering Algebraic Simplification
Simplifying algebraic expressions is a fundamental skill in mathematics. By understanding the concepts of like terms, the commutative and associative properties, and the step-by-step process, you can confidently tackle a wide range of algebraic problems. Remember to practice regularly, and don't hesitate to seek help when needed. With consistent effort, you'll master this crucial skill and build a strong foundation for more advanced algebraic concepts. The seemingly simple act of simplifying 1 + 2x + 1 + 2 opens the door to a much wider world of mathematical possibilities. Remember, the key is to break down complex problems into smaller, manageable steps, and with practice, you'll become proficient in simplifying even the most challenging algebraic expressions.
Latest Posts
Latest Posts
-
16 Oz Is A Lb
Sep 15, 2025
-
What Is 2 5 Equivalent To
Sep 15, 2025
-
90 Confidence Interval Z Score
Sep 15, 2025
-
How Do You Spell Vicious
Sep 15, 2025
-
Structure And Plot Quick Check
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Simplify 1 2x 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.