Solve 4x 3 2x 7
cibeltiagestion
Sep 16, 2025 · 6 min read
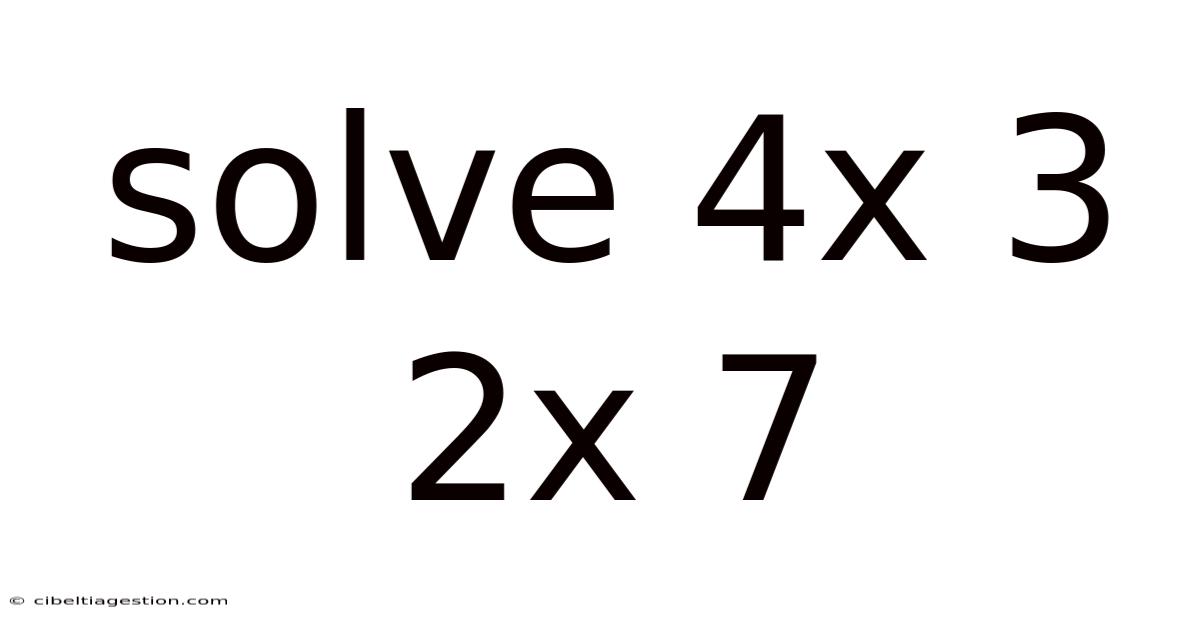
Table of Contents
Solving the Equation 4x³ + 2x = 7: A Comprehensive Guide
This article provides a detailed walkthrough of solving the cubic equation 4x³ + 2x = 7. We'll explore various methods, from the straightforward (but potentially lengthy) process of using the cubic formula to more practical approaches involving numerical methods. Understanding how to solve cubic equations is crucial in various fields, including engineering, physics, and computer science. This guide will equip you with the knowledge and tools to tackle similar problems effectively. We will explore both the theoretical underpinnings and practical application of solving this specific cubic equation.
1. Introduction: Understanding Cubic Equations
A cubic equation is a polynomial equation of degree three, meaning the highest power of the variable (in this case, x) is 3. The general form of a cubic equation is:
ax³ + bx² + cx + d = 0
where a, b, c, and d are constants, and a ≠ 0. Our equation, 4x³ + 2x = 7, needs to be rearranged into this standard form before we can begin solving.
2. Rearranging the Equation
The first step is to rewrite the equation in the standard form of a cubic equation. To do this, we subtract 7 from both sides:
4x³ + 2x - 7 = 0
Now we have the equation in the standard form, where a = 4, b = 0, c = 2, and d = -7.
3. Solving Using the Cubic Formula (Cardano's Method)
The cubic formula, also known as Cardano's formula, provides a direct way to solve cubic equations. However, it's a complex and lengthy process, often involving complex numbers even when the final solutions are real. Let's briefly outline the steps, but we will focus on more practical methods later.
The cubic formula involves calculating the following:
- Δ₀ = b² - 3ac
- Δ₁ = 2b³ - 9abc + 27a²d
- C = ³√((-Δ₁ ± √(Δ₁² - 4Δ₀³))/2)
- x = -b/(3a) + C - Δ₀/(3aC)
Applying these steps to our equation (4x³ + 2x - 7 = 0) would involve substantial calculations. While this method provides an exact solution, the complexity makes it less practical for hand calculations. For this reason, we'll explore more manageable approaches.
4. Numerical Methods: Approximating the Solution
Numerical methods offer efficient ways to approximate solutions to cubic equations, especially when the analytical solution is cumbersome. Two common numerical methods are the Newton-Raphson method and the bisection method.
4.1 Newton-Raphson Method:
The Newton-Raphson method is an iterative method that refines an initial guess to find a closer approximation of the root. The iterative formula is:
xₙ₊₁ = xₙ - f(xₙ) / f'(xₙ)
where:
- xₙ is the current approximation
- xₙ₊₁ is the next approximation
- f(x) is the function (in our case, 4x³ + 2x - 7)
- f'(x) is the derivative of the function (12x² + 2)
To use this method:
- Make an initial guess: Let's start with x₀ = 1.
- Calculate f(x₀) and f'(x₀): f(1) = 4(1)³ + 2(1) - 7 = -1 f'(1) = 12(1)² + 2 = 14
- Apply the iterative formula: x₁ = 1 - (-1) / 14 ≈ 1.0714
- Repeat steps 2 and 3: Continue iterating until the desired level of accuracy is achieved. The iterations will converge towards a root.
This method requires an initial guess and can converge to different roots depending on the initial guess. Multiple iterations are necessary for increased accuracy.
4.2 Bisection Method:
The bisection method is another iterative approach that relies on finding an interval where the root lies. It works by repeatedly halving the interval until the root is approximated within a desired tolerance.
- Find an interval: Observe that f(1) = -1 and f(2) = 25. Since the function changes sign between x = 1 and x = 2, a root must lie within this interval.
- Bisect the interval: Find the midpoint: x = (1 + 2) / 2 = 1.5
- Evaluate f(x): f(1.5) ≈ 7.75.
- Reduce the interval: Since f(1.5) is positive, the root must lie between 1 and 1.5. Repeat the process by bisecting this new interval.
- Iterate: Continue bisecting the interval until the desired accuracy is reached.
The bisection method is slower than the Newton-Raphson method but guarantees convergence if a root exists within the initial interval.
5. Graphical Method: Visualizing the Solution
A graphical approach can provide a visual representation of the solution. Plotting the function y = 4x³ + 2x - 7 will show the x-intercept(s), which represent the root(s) of the equation. Using graphing software or a calculator, you can observe the approximate value of the root. This method is excellent for obtaining a quick visual estimate, but it is not as precise as numerical methods for determining the exact value.
6. Using a Calculator or Software
Most scientific calculators and mathematical software packages (such as MATLAB, Wolfram Alpha, or others) have built-in functions to solve cubic equations directly. These tools provide a convenient and accurate way to find the root(s) of the equation. Simply input the coefficients (a=4, b=0, c=2, d=-7) and the software will provide the solution(s).
7. Explanation of the Solution(s)
The equation 4x³ + 2x - 7 = 0 has only one real root. While the cubic formula could be used to find this root (along with two complex roots), the numerical methods offer more practical and efficient ways to solve this particular cubic equation. The approximate real root is around x ≈ 1.1. The exact value requires a high degree of precision and is best found using computational tools. This single real root signifies the x-value where the function intersects the x-axis. The other two roots are complex conjugates (involving the imaginary unit 'i').
8. Frequently Asked Questions (FAQ)
-
Q: Why are numerical methods preferred for this equation? A: The cubic formula, while providing an exact solution, is complex and prone to errors when calculated manually. Numerical methods offer a more practical approach, especially when approximations are sufficient.
-
Q: Can there be more than one real root for a cubic equation? A: Yes, a cubic equation can have one, two, or three real roots. The number of real roots depends on the coefficients of the equation.
-
Q: What if I don't have access to a calculator or software? A: The bisection method is a relatively simple iterative method that requires only basic arithmetic and can be performed manually, although it will be slower and potentially less accurate than other methods.
-
Q: What is the significance of finding the roots of a cubic equation? A: Finding the roots of a cubic equation is crucial in many applications, including finding equilibrium points in physical systems, determining the roots of polynomial equations in engineering, and solving problems in various scientific fields.
9. Conclusion: Mastering Cubic Equation Solutions
Solving cubic equations like 4x³ + 2x = 7 requires a comprehensive understanding of different approaches. While the cubic formula provides a direct, albeit complex, solution, numerical methods such as the Newton-Raphson and bisection methods offer practical alternatives. Graphical methods offer a visual understanding, and computational tools provide accurate and efficient solutions. The choice of method depends on the desired level of accuracy, available resources, and the complexity of the equation. By understanding these different approaches, you're well-equipped to tackle similar problems confidently. Remember to always consider the context of the problem and choose the most suitable method accordingly. This deep dive into solving 4x³ + 2x = 7 provides a solid foundation for tackling other cubic equation challenges you may encounter.
Latest Posts
Related Post
Thank you for visiting our website which covers about Solve 4x 3 2x 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.