Square Root Of 3 8
cibeltiagestion
Sep 11, 2025 · 6 min read
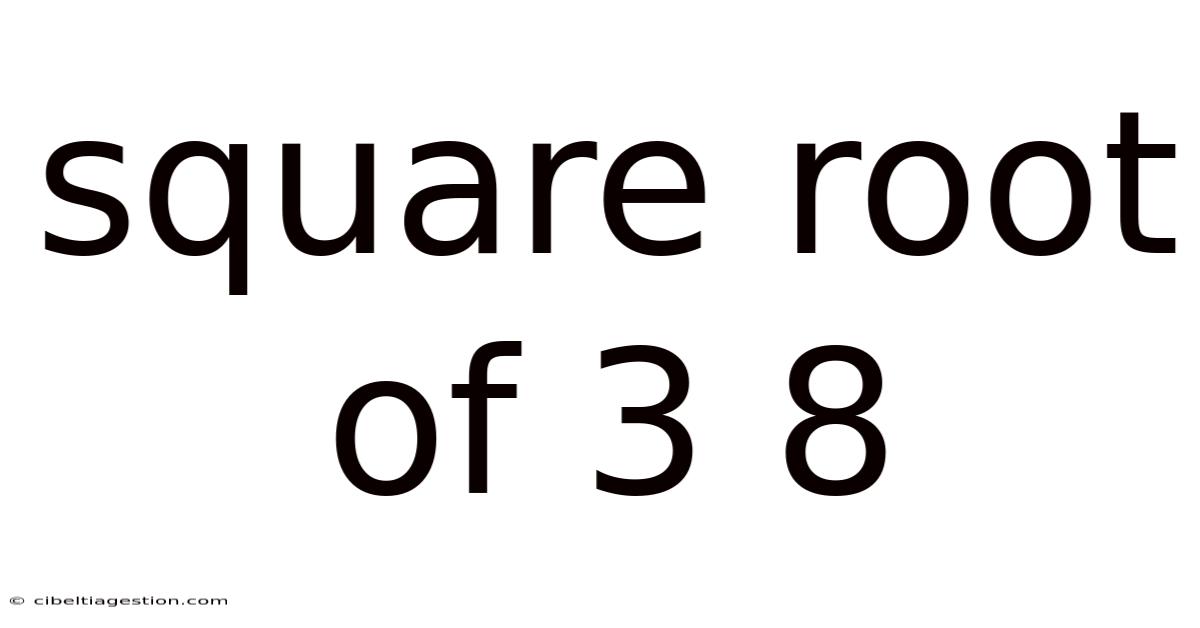
Table of Contents
Unveiling the Mysteries of the Square Root of 38: A Comprehensive Guide
The square root of 38, denoted as √38, might seem like a simple mathematical concept at first glance. However, delving into its intricacies reveals a fascinating journey into the world of irrational numbers, approximation techniques, and the practical applications of this seemingly abstract value. This comprehensive guide will explore the square root of 38 from its basic definition to its advanced applications, providing a clear understanding for learners of all levels. We'll cover methods for calculating it, its significance in different fields, and answer frequently asked questions.
Understanding Square Roots: A Quick Recap
Before we dive into the specifics of √38, let's refresh our understanding of square roots. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3, because 3 x 3 = 9. Square roots can be represented symbolically using the radical symbol (√) or as a fractional exponent (e.g., 38<sup>1/2</sup>).
Calculating the Square Root of 38: Methods and Approximations
Unlike perfect squares (like 9, 16, 25, etc.), 38 doesn't have a whole number square root. This means √38 is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation continues infinitely without repeating. However, we can find approximations using various methods.
1. Using a Calculator: The Easiest Approach
The simplest way to find an approximation for √38 is to use a calculator. Most calculators have a square root function (√). Simply input 38 and press the square root button. You'll obtain an approximation like 6.164414...
2. The Babylonian Method (or Heron's Method): An Iterative Approach
This ancient method provides a way to iteratively refine an approximation. It involves starting with an initial guess and repeatedly refining it using the formula:
x<sub>n+1</sub> = ½(x<sub>n</sub> + 38/x<sub>n</sub>)
where:
- x<sub>n</sub> is the current approximation
- x<sub>n+1</sub> is the improved approximation
Let's demonstrate:
-
Initial Guess: Let's start with x<sub>0</sub> = 6 (since 6² = 36, which is close to 38).
-
First Iteration: x<sub>1</sub> = ½(6 + 38/6) ≈ 6.1667
-
Second Iteration: x<sub>2</sub> = ½(6.1667 + 38/6.1667) ≈ 6.1644
With each iteration, the approximation gets closer to the actual value. You can continue this process until you reach the desired level of accuracy.
3. Linear Approximation: A Simpler, Less Precise Method
For a quick, less precise approximation, we can use linear approximation. We know that √36 = 6 and √49 = 7. Since 38 is between 36 and 49, √38 will be between 6 and 7. We can use a linear interpolation to estimate:
√38 ≈ 6 + (38 - 36)/(49 - 36) * (7 - 6) ≈ 6.18
This method is less accurate than the Babylonian method but provides a reasonable estimate with minimal calculation.
The Significance of √38: Applications in Various Fields
While √38 might not be as frequently encountered as simpler square roots, it appears in various mathematical and scientific applications, often within more complex calculations. Here are some examples:
-
Geometry: Calculations involving triangles, particularly those using the Pythagorean theorem (a² + b² = c²), may involve the square root of 38. For instance, if two sides of a right-angled triangle measure a certain length and the hypotenuse length requires solving the equation c² = a² + b², resulting in a value like 38, the calculation would directly involve finding √38.
-
Physics: Many physical formulas involve square roots, making √38 potentially relevant in various scenarios depending on the equations utilized. For example, calculations related to velocity, energy, or other physical quantities might incorporate this value.
-
Engineering: Similar to physics, engineering applications often rely on formulas that utilize square roots, leading to instances where √38 could be encountered.
-
Statistics: Statistical calculations involving standard deviations and other measures of dispersion can result in values that require taking the square root. While not a direct application of √38, the principle remains similar.
-
Computer Graphics: In computer graphics and game development, the square root is often used for distance calculations and normalization of vectors. While it's usually handled by optimized computer functions, the mathematical principle is fundamental.
The Irrational Nature of √38: A Deeper Dive
As mentioned earlier, √38 is an irrational number. This means it cannot be expressed as a fraction of two integers (a/b where a and b are integers, and b ≠ 0). The decimal representation of √38 is non-terminating and non-repeating. This irrationality arises from the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely factored into prime numbers. Since 38 = 2 x 19 (both prime numbers), its square root doesn't have a simple rational form.
Beyond Approximation: Understanding the Continued Fraction Representation
While decimal approximations are useful, the continued fraction representation offers another way to understand and express irrational numbers like √38. A continued fraction represents a number as a sum of a whole number and the reciprocal of another whole number, and so on. The continued fraction for √38 is quite complex and involves an infinite sequence. This representation provides a unique and potentially more efficient way to approximate the number compared to other methods. The process of generating the continued fraction for a square root is based on a recursive algorithm. While beyond the scope of this introductory guide, researching continued fraction representations offers insights into advanced number theory.
Frequently Asked Questions (FAQs)
Q1: Is there a way to find the exact value of √38?
A1: No. The exact value of √38 is an irrational number, meaning its decimal representation is infinite and non-repeating. We can only find increasingly accurate approximations.
Q2: What is the difference between √38 and -√38?
A2: Both √38 and -√38 are square roots of 38. The principal square root (√38) is the positive value, while -√38 is the negative counterpart. Both values, when squared, result in 38.
Q3: How can I calculate √38 without a calculator?
A3: You can use methods like the Babylonian method or linear approximation (as explained above) to calculate approximations without a calculator. However, these methods require iterative calculations and will not provide the exact value.
Q4: Are there any real-world scenarios where I would need to calculate √38 precisely?
A4: While perfectly precise calculations of √38 might not be frequently necessary in everyday life, approximations are often sufficient for various practical applications in geometry, physics, engineering, and more. The underlying mathematical concept is crucial for understanding these fields.
Conclusion: Embracing the Beauty of Irrational Numbers
The square root of 38, despite its seemingly simple appearance, is a gateway to understanding the world of irrational numbers and the beauty of infinite, non-repeating decimal expansions. While we can't pinpoint its exact value, various methods allow us to find increasingly accurate approximations, sufficient for many practical applications. From the ancient Babylonian method to modern calculators, the quest to understand and approximate √38 highlights the enduring power of mathematics and its capacity to unravel the complexities of the world around us. Through this journey, we appreciate not just the numerical value, but the rich mathematical concepts it embodies and its surprising relevance across various scientific and engineering disciplines. Understanding concepts like irrational numbers and approximation techniques is crucial for building a strong foundation in mathematics and science.
Latest Posts
Latest Posts
-
Simplify 9 X 7 X
Sep 11, 2025
-
Market Saturation Results From Excess
Sep 11, 2025
-
How Many Oz Is 30g
Sep 11, 2025
-
Which Sentence Contains A Metaphor
Sep 11, 2025
-
1 2 Of 3 4 Cup Sugar
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 3 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.