Square Root Of 80 Simplified
cibeltiagestion
Sep 05, 2025 · 5 min read
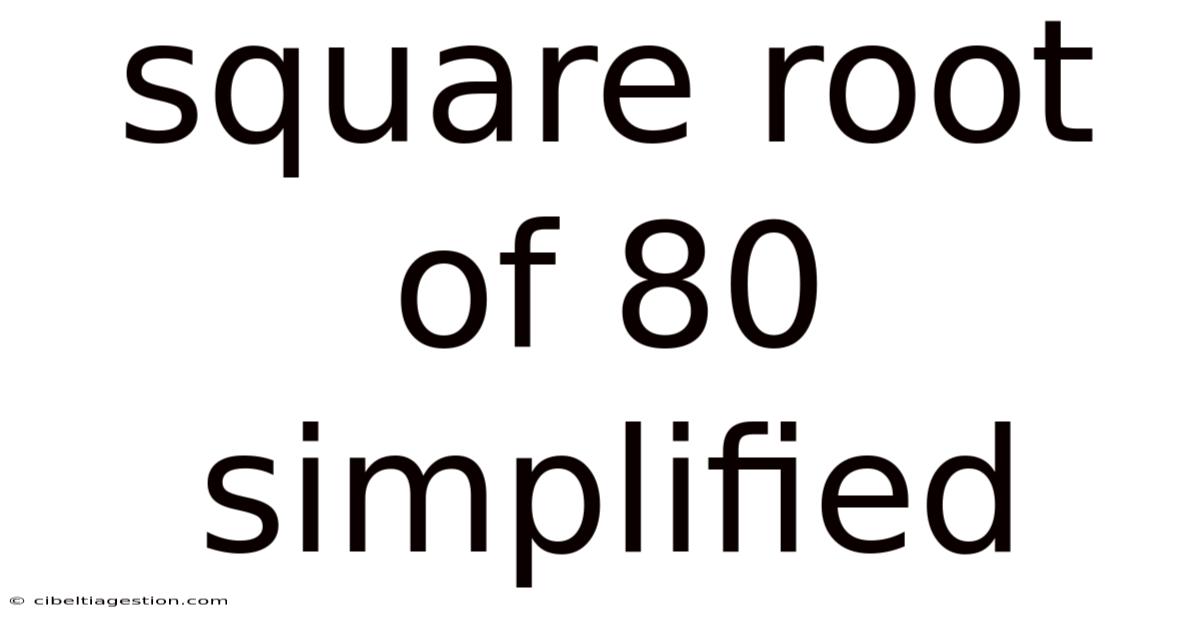
Table of Contents
Simplifying the Square Root of 80: A Comprehensive Guide
Understanding how to simplify square roots is a fundamental skill in mathematics, particularly in algebra and beyond. This comprehensive guide will walk you through the process of simplifying the square root of 80, √80, exploring the underlying concepts and providing a step-by-step approach. We’ll delve into the prime factorization method, explain the reasoning behind each step, and even address some frequently asked questions. By the end, you'll not only know the simplified form of √80 but also possess a strong grasp of simplifying square roots in general.
Introduction: What Does it Mean to Simplify a Square Root?
Simplifying a square root means expressing it in its most reduced form. A simplified square root has no perfect square factors other than 1 remaining under the radical symbol (√). For example, √12 can be simplified because 12 contains the perfect square factor 4 (12 = 4 x 3). Therefore, √12 simplifies to 2√3 because √4 = 2. Our goal with √80 is to find all perfect square factors and remove them from under the radical.
Understanding Prime Factorization
The key to simplifying square roots efficiently is prime factorization. Prime factorization is the process of breaking down a number into its prime factors – numbers that are only divisible by 1 and themselves. Prime numbers less than 20 include 2, 3, 5, 7, 11, 13, 17, and 19.
Let’s find the prime factorization of 80:
- Start with the smallest prime number, 2: 80 is divisible by 2, resulting in 40.
- Continue dividing by 2: 40 divided by 2 is 20; 20 divided by 2 is 10; 10 divided by 2 is 5.
- Now, we've reached a prime number (5): The prime factorization of 80 is 2 x 2 x 2 x 2 x 5, or 2⁴ x 5.
Simplifying √80: A Step-by-Step Approach
Now that we know the prime factorization of 80 (2⁴ x 5), we can simplify √80:
- Rewrite the square root using the prime factorization: √(2⁴ x 5)
- Separate the terms under the radical: √2⁴ x √5
- Simplify the perfect square: Remember that √a² = a. Therefore, √2⁴ = √(2²)² = 2². This simplifies to 4.
- Combine the simplified terms: 4√5
Therefore, the simplified form of √80 is 4√5.
Visualizing the Simplification
Imagine you have 80 identical square tiles. You want to arrange them into the largest possible square. You could arrange them in a 10 x 8 rectangle, but this isn't a square. To make a square, we need to find the largest perfect square that divides 80.
Through prime factorization, we discovered that 80 = 16 x 5. 16 is a perfect square (4 x 4), so we can arrange 16 tiles into a 4 x 4 square. This leaves 5 tiles that cannot be arranged into a larger square. Therefore, we have one 4 x 4 square (representing 4√5), and 5 single tiles left over (represented by the √5).
Further Examples of Simplifying Square Roots
Let's solidify our understanding with a few more examples:
- √72: The prime factorization of 72 is 2³ x 3². This simplifies to √(2² x 2 x 3²) = √2² x √3² x √2 = 2 x 3 x √2 = 6√2
- √125: The prime factorization of 125 is 5³. This simplifies to √(5² x 5) = √5² x √5 = 5√5
- √147: The prime factorization of 147 is 3 x 7². This simplifies to √(3 x 7²) = √7² x √3 = 7√3
- √200: The prime factorization of 200 is 2³ x 5². This simplifies to √(2² x 2 x 5²) = √2² x √5² x √2 = 2 x 5 x √2 = 10√2
Working with Variables in Square Roots
The principles of simplification also extend to square roots involving variables. For instance:
- √x⁶: This simplifies to x³ because √x⁶ = √(x³)² = x³
- √(4x²y⁴): This simplifies to 2xy² because √(4x²y⁴) = √(2² x x² x (y²)²) = 2xy²
- √(18a⁴b³): The prime factorization of 18 is 2 x 3². Therefore, √(18a⁴b³) = √(2 x 3² x a⁴ x b²) x √b = 3a²b√(2b)
Frequently Asked Questions (FAQ)
Q: Why is simplifying square roots important?
A: Simplifying square roots is crucial for several reasons. First, it presents the answer in its most concise and understandable form. Secondly, it's essential for further mathematical operations. For example, adding or subtracting square roots requires them to be in their simplest form.
Q: What if I get a different prime factorization?
A: The prime factorization of a number is unique (except for the order of the factors). If you arrive at a different factorization, double-check your work. You might have missed a prime factor or made a calculation error. However, regardless of the order, your simplified square root should be the same.
Q: Can I simplify a square root by dividing under the radical?
A: No, you cannot directly divide numbers under the radical to simplify a square root. The operation should always focus on finding and extracting perfect squares.
Q: Can I use a calculator to simplify square roots?
A: While calculators can provide decimal approximations, they don't always give the simplified radical form. Learning the method of prime factorization is crucial for understanding the underlying mathematical principles.
Conclusion: Mastering Square Root Simplification
Simplifying square roots like √80 is a valuable skill that builds a stronger mathematical foundation. By understanding prime factorization and applying the step-by-step method explained above, you can confidently simplify any square root. Remember, practice is key. The more you work through examples, the more comfortable and proficient you'll become. Now you not only know that √80 simplifies to 4√5 but also understand the why behind the process. This knowledge will serve you well in your future mathematical endeavors.
Latest Posts
Latest Posts
-
What Is 20 Of 14
Sep 05, 2025
-
Mr Alonso Receives Some Help
Sep 05, 2025
-
Sealed Combustion Oil Furnaces Use
Sep 05, 2025
-
Shakespearean Sonnets Are Organized In
Sep 05, 2025
-
What Is A Circuit System Verification
Sep 05, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 80 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.