What Is 10 Of 110
cibeltiagestion
Sep 12, 2025 · 5 min read
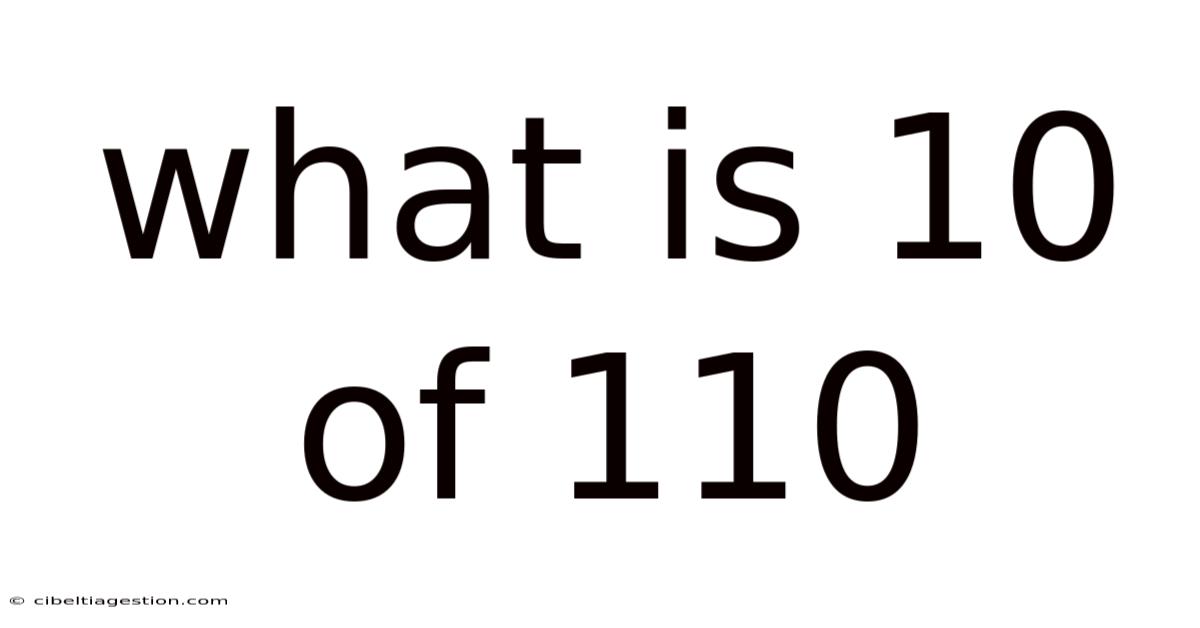
Table of Contents
What is 10% of 110? Understanding Percentages and Their Applications
This article will delve into the seemingly simple question: "What is 10% of 110?" While the answer might seem immediately obvious to some, understanding the underlying principles of percentages is crucial for various applications in everyday life, from calculating discounts to understanding financial reports. We'll explore the calculation itself, discuss different methods for solving percentage problems, and explore real-world examples to solidify your understanding. This guide is designed for everyone, from those brushing up on basic math to those seeking a deeper comprehension of percentages.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." So, 10% means 10 out of 100, or 10/100, which simplifies to 1/10. This fundamental understanding is key to solving percentage problems.
Calculating 10% of 110: The Simple Method
The most straightforward method to calculate 10% of 110 involves converting the percentage to a decimal and then multiplying.
-
Convert the percentage to a decimal: 10% is equivalent to 0.10 (simply divide the percentage by 100).
-
Multiply the decimal by the number: 0.10 * 110 = 11
Therefore, 10% of 110 is 11.
Alternative Methods: Proportion and Fraction
While the decimal method is efficient, understanding alternative approaches provides a broader mathematical perspective.
Method 1: Using Proportion
A proportion sets up an equivalence between two ratios. We can set up a proportion to solve for x, where x represents 10% of 110:
10/100 = x/110
To solve for x, we cross-multiply:
10 * 110 = 100 * x
1100 = 100x
x = 1100/100
x = 11
Method 2: Using Fractions
As mentioned earlier, 10% is equivalent to the fraction 1/10. Therefore, we can calculate 10% of 110 as follows:
(1/10) * 110 = 11
Both the proportion and fraction methods arrive at the same answer: 11.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-world scenarios:
-
Discounts: Imagine a store offering a 10% discount on an item priced at $110. Using the knowledge gained, you can quickly determine the discount amount ($11) and the final price ($99).
-
Taxes: Calculating sales tax or income tax involves percentage calculations. If the sales tax is 6%, for example, you'll need to calculate the tax amount on a purchase before determining the total cost.
-
Tips: Determining a tip amount at a restaurant often requires calculating a percentage of the total bill. A 15% tip on a $50 meal, for instance, would be $7.50.
-
Financial Analysis: Percentage changes are used extensively in finance to track growth, losses, and returns on investments. For example, understanding percentage increases or decreases in stock prices is essential for informed investing.
-
Statistics: Percentages are frequently used in statistical analysis to represent proportions within a dataset. Understanding these proportions is crucial for interpreting data and drawing conclusions.
-
Science and Engineering: Many scientific and engineering applications utilize percentages to represent concentrations, efficiencies, or error rates. For instance, the percentage of a certain chemical in a solution or the percentage efficiency of a machine are crucial parameters.
Beyond the Basics: Calculating Other Percentages of 110
Let's expand our understanding by calculating different percentages of 110:
- 20% of 110: (0.20 * 110) = 22
- 25% of 110: (0.25 * 110) = 27.5
- 50% of 110: (0.50 * 110) = 55
- 75% of 110: (0.75 * 110) = 82.5
- 100% of 110: (1.00 * 110) = 110
Working Backwards: Finding the Original Number
Understanding percentages also involves working backward. Suppose you know that 10% of a number is 11. How do you find the original number?
We can set up a simple equation:
0.10 * x = 11
To solve for x, divide both sides by 0.10:
x = 11 / 0.10
x = 110
This demonstrates the inverse relationship between percentages and the original number.
Dealing with More Complex Percentages
While the examples above focus on simple percentages, calculating more complex percentages follows the same principles. For example, to calculate 17.5% of 110:
(0.175 * 110) = 19.25
Frequently Asked Questions (FAQ)
Q1: What is the easiest way to calculate percentages?
A1: The easiest method is usually converting the percentage to a decimal and multiplying it by the number.
Q2: How do I calculate percentages without a calculator?
A2: For simple percentages like 10%, 25%, or 50%, you can often perform mental calculations using fractions. For more complex percentages, you can use the proportion method or break the percentage into smaller, manageable parts.
Q3: Are there any online tools to help with percentage calculations?
A3: Many online calculators and websites are available to assist with percentage calculations. These tools can be particularly helpful for more complex problems.
Q4: Why is understanding percentages important?
A4: Understanding percentages is crucial for numerous everyday tasks, from managing finances and shopping to interpreting data and understanding scientific concepts.
Conclusion
The answer to "What is 10% of 110?" is unequivocally 11. This seemingly simple question serves as a gateway to understanding the broader concept of percentages and their wide-ranging applications. By mastering various methods of calculation and appreciating the real-world relevance of percentages, you equip yourself with a valuable tool for navigating numerous aspects of daily life and professional endeavors. Remember, the key is to understand the fundamental principle – a percentage represents a fraction of 100 – and apply this understanding to solve various percentage-related problems. Practice is key to mastering this essential mathematical skill.
Latest Posts
Latest Posts
-
Geometry Unit 3 Homework 2
Sep 12, 2025
-
Given Pqrs Solve For X
Sep 12, 2025
-
Lmn Is A Right Triangle
Sep 12, 2025
-
What Is 30 Of 45
Sep 12, 2025
-
Gcf Of 16 And 32
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 110 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.