What Is 10 Of 120
cibeltiagestion
Sep 12, 2025 · 5 min read
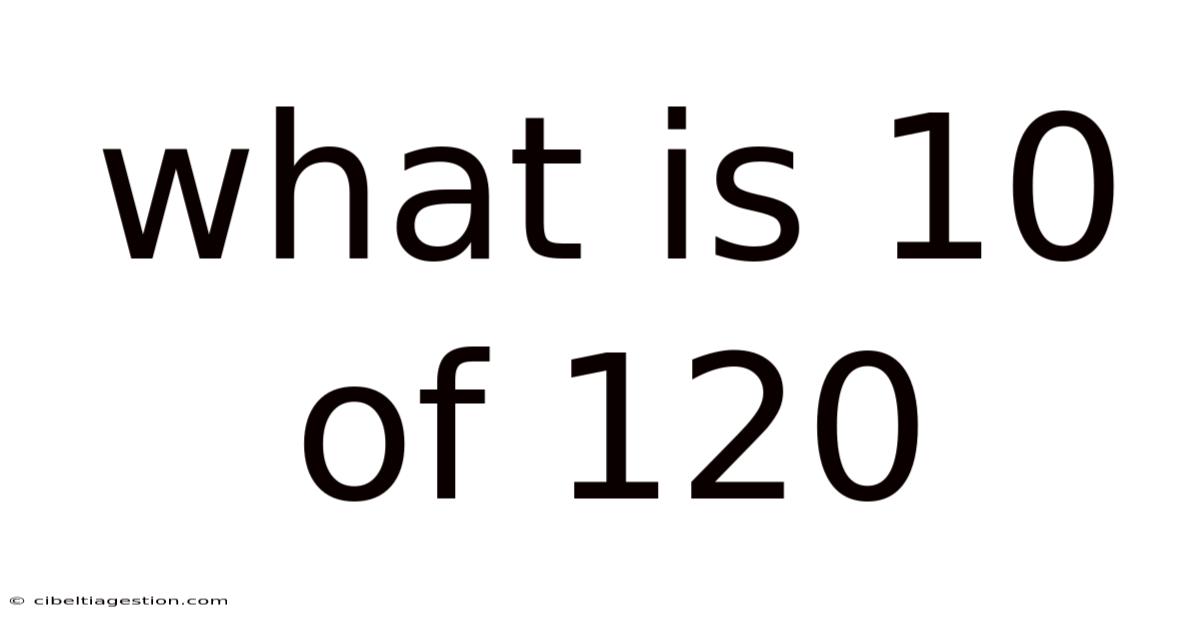
Table of Contents
What is 10% of 120? A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to comprehending statistical data and financial reports. This article will delve into the question, "What is 10% of 120?", providing not just the answer but a comprehensive exploration of the underlying concepts, methods of calculation, and real-world examples. We'll also explore different approaches to solving percentage problems, ensuring you gain a solid grasp of this essential mathematical concept.
Introduction: Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100" ("per" meaning "for each" and "cent" meaning "hundred"). Therefore, 10% means 10 out of 100, or 10/100, which simplifies to 1/10. Percentages are a convenient way to represent proportions and ratios, making comparisons easier to understand.
Calculating 10% of 120: The Basic Method
The most straightforward method to find 10% of 120 involves converting the percentage to a decimal and then multiplying.
-
Convert the percentage to a decimal: To convert 10% to a decimal, divide by 100: 10% ÷ 100 = 0.10 (or simply 0.1)
-
Multiply the decimal by the number: Multiply the decimal (0.1) by 120: 0.1 * 120 = 12
Therefore, 10% of 120 is 12.
Alternative Methods: Different Approaches to the Same Solution
While the above method is the most common, several alternative approaches can be used to calculate percentages, particularly useful for mental calculations or when dealing with specific percentages.
-
Using Fractions: As mentioned earlier, 10% is equivalent to the fraction 1/10. Therefore, finding 10% of 120 is the same as finding 1/10 of 120. This simply involves dividing 120 by 10: 120 ÷ 10 = 12. This method is particularly helpful for percentages like 10%, 25%, 50%, and other easily converted fractions.
-
Using Proportions: Percentages can be solved using proportions. We can set up a proportion like this:
x/120 = 10/100
Solving for x (10% of 120):
x = (10/100) * 120 = 12
This method is more versatile and can be applied to more complex percentage problems.
- Mental Calculation Techniques: For 10%, simply moving the decimal point one place to the left gives you the answer. In the case of 120, moving the decimal point one place to the left gives you 12.0, or 12. This shortcut is applicable only for calculating 10% of a number.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is vital in various real-world scenarios. Here are some examples:
-
Discounts and Sales: Stores frequently offer discounts on products. For example, a 10% discount on a $120 item would mean a saving of $12 (10% of 120).
-
Taxes: Sales tax is a percentage added to the price of goods and services. Understanding percentages allows you to calculate the total cost including tax.
-
Tips and Gratuities: Calculating tips in restaurants or service charges involves determining a percentage of the bill.
-
Financial Calculations: Percentages are crucial in finance, used to calculate interest rates, loan repayments, investment returns, and more.
-
Statistics and Data Analysis: Percentages are used extensively to represent data in graphs, charts, and reports. For example, the percentage of students who passed an exam or the percentage market share of a company.
-
Scientific Applications: Percentages are used to express concentrations in chemistry, error margins in experiments, and various other scientific computations.
Solving More Complex Percentage Problems
The techniques discussed above can be extended to solve more complex percentage problems. For example:
-
Finding a number given a percentage: If you know that 10% of a number is 12, you can find the original number by dividing 12 by 0.10 (or multiplying by 10): 12 ÷ 0.10 = 120.
-
Finding the percentage increase or decrease: Suppose the price of an item increases from $100 to $120. The percentage increase can be calculated as follows:
- Find the difference: $120 - $100 = $20
- Divide the difference by the original price: $20/$100 = 0.20
- Multiply by 100 to express as a percentage: 0.20 * 100 = 20%
-
Calculating percentage change over time: This involves calculating percentage changes over multiple periods, often used in financial analysis and economic indicators. For instance, tracking the growth of a company's revenue over several years.
Frequently Asked Questions (FAQ)
-
What if I need to calculate a different percentage of 120? Simply replace 0.10 (or 10/100) with the desired percentage expressed as a decimal in the multiplication step. For example, to find 25% of 120, multiply 120 by 0.25.
-
How can I improve my speed in calculating percentages? Practice is key. Regularly solving percentage problems, including various types and complexities, will improve your calculation speed and accuracy. You can also try memorizing the decimal equivalents of common percentages, like 25% (0.25), 50% (0.50), etc.
-
Are there any online tools or calculators for percentages? Yes, many online calculators are available that can help calculate percentages quickly and easily. However, understanding the underlying principles is crucial for independent problem-solving.
-
What are the applications of percentages in higher-level mathematics? Percentages are fundamental in various higher-level mathematical concepts, including calculus, probability, and statistics.
Conclusion: Mastering Percentage Calculations
Calculating percentages, while seemingly simple, is a crucial skill with vast real-world applications. Understanding the basic methods and various approaches allows you to tackle a wide range of problems efficiently and accurately. Beyond the simple calculation of 10% of 120, this article has provided you with a comprehensive understanding of percentages, enabling you to confidently approach and solve various percentage-related challenges in your academic and professional life. Remember, consistent practice is the key to mastering this essential mathematical concept. By understanding the underlying principles and practicing regularly, you can build confidence and competence in handling any percentage-related problem that comes your way.
Latest Posts
Latest Posts
-
Which Component Creates Hydraulic Pressure
Sep 12, 2025
-
The Term Realism Refers To
Sep 12, 2025
-
Which Inequality Is Equivalent To
Sep 12, 2025
-
Period 4 Alkaline Earth Metal
Sep 12, 2025
-
Find X In Circle O
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.