What Is 10 Of 35
cibeltiagestion
Sep 01, 2025 · 6 min read
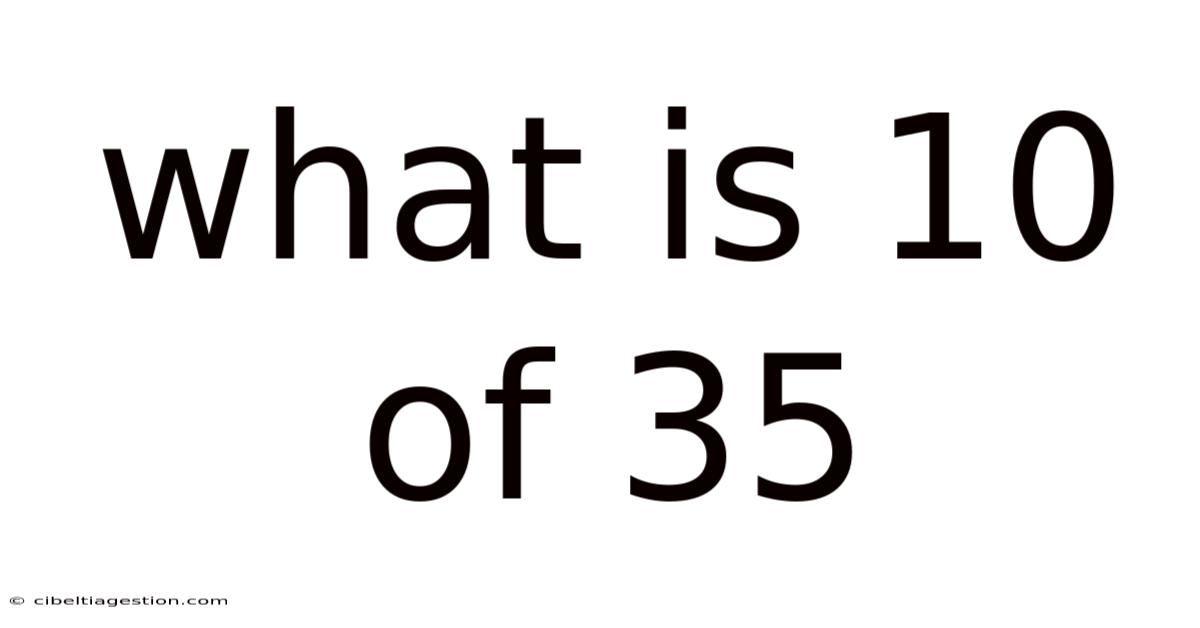
Table of Contents
What is 10 of 35? Deconstructing Fractions, Percentages, and Ratios
This article explores the multifaceted meaning of "10 of 35," examining it through the lenses of fractions, percentages, and ratios. We'll delve into the calculations, explore practical applications, and even touch upon the underlying mathematical principles. Understanding "10 of 35" is not just about a simple calculation; it's about grasping fundamental mathematical concepts applicable across numerous fields.
Understanding the Fundamentals: Fractions, Percentages, and Ratios
Before we tackle "10 of 35," let's establish a solid foundation in the key mathematical concepts involved.
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts considered, while the denominator represents the total number of parts in the whole. For example, ½ represents one part out of two equal parts.
Percentages: A percentage is a fraction expressed as a portion of 100. It indicates how many parts out of 100 constitute a specific quantity. The symbol "%" denotes percentage. For instance, 50% represents 50 parts out of 100, which is equivalent to ½.
Ratios: A ratio compares two or more quantities. It shows the relative size of one quantity compared to another. Ratios can be expressed using a colon (e.g., 1:2) or as a fraction (e.g., 1/2). A ratio of 1:2 means there's one part of the first quantity for every two parts of the second quantity.
Calculating 10 of 35: The Fraction Approach
The phrase "10 of 35" directly translates into the fraction 10/35. This fraction represents 10 parts out of a total of 35 parts. To simplify this fraction, we find the greatest common divisor (GCD) of 10 and 35, which is 5. Dividing both the numerator and the denominator by 5, we get:
10/35 = (10 ÷ 5) / (35 ÷ 5) = 2/7
Therefore, 10 out of 35 is equivalent to 2/7. This simplified fraction represents the simplest form of the ratio between 10 and 35.
Calculating 10 of 35: The Percentage Approach
To express "10 of 35" as a percentage, we first convert the fraction 10/35 to a decimal. We divide the numerator (10) by the denominator (35):
10 ÷ 35 ≈ 0.2857
To convert this decimal to a percentage, we multiply by 100:
0.2857 x 100 ≈ 28.57%
Therefore, 10 out of 35 is approximately 28.57%. Note that this is an approximation because the decimal representation of 2/7 is non-terminating.
Calculating 10 of 35: The Ratio Approach
The ratio approach simply expresses the relationship between 10 and 35. We can write this as:
10:35
Similar to the fraction approach, we can simplify this ratio by dividing both numbers by their GCD (5):
10:35 = (10 ÷ 5):(35 ÷ 5) = 2:7
Thus, the ratio of 10 to 35 simplifies to 2:7. This indicates that for every 2 parts of one quantity, there are 7 parts of the other.
Practical Applications of Understanding "10 of 35"
The concept of "10 of 35" and its various representations – fraction, percentage, and ratio – has numerous practical applications across diverse fields:
-
Statistics and Probability: Imagine a survey where 10 out of 35 respondents chose a particular option. Understanding the fraction (2/7), percentage (28.57%), and ratio (2:7) allows for easy interpretation and comparison of the results.
-
Business and Finance: Suppose a company sold 10 units out of a total of 35 units produced. These figures help in calculating sales efficiency, production ratios, and inventory management.
-
Everyday Life: Imagine you have 35 candies, and you give 10 to your friend. Understanding the fraction, percentage, and ratio helps in visualizing the portion shared and the portion retained.
-
Science and Engineering: In scientific experiments, data often involves ratios and percentages. For example, if 10 out of 35 samples showed a particular reaction, the fraction, percentage, and ratio provide a clear representation of the experimental results.
Beyond the Basics: Exploring Further Mathematical Concepts
The seemingly simple problem of "10 of 35" opens doors to exploring several advanced mathematical concepts:
-
Proportionality: The relationship between 10 and 35 is proportional. This means that if we increase or decrease one value, the other value changes proportionally.
-
Equivalent Fractions: We saw that 10/35 is equivalent to 2/7. Understanding equivalent fractions helps in simplifying complex calculations and making comparisons easier.
-
Decimal Representation: Converting fractions to decimals is crucial in many mathematical and scientific applications. The decimal representation of 2/7 (approximately 0.2857) highlights the importance of understanding both exact and approximate values.
-
Percentage Calculations: Mastering percentage calculations is vital in various aspects of life, from calculating discounts to understanding interest rates. Knowing how to convert fractions to percentages and vice versa expands your problem-solving abilities.
Frequently Asked Questions (FAQ)
Q1: Is there only one way to represent "10 of 35"?
A1: No, there are multiple ways to represent "10 of 35," including as a fraction (10/35 or 2/7), a percentage (approximately 28.57%), and a ratio (10:35 or 2:7). The best representation depends on the specific context and the information you want to convey.
Q2: Why is simplifying fractions important?
A2: Simplifying fractions makes them easier to understand and compare. It also makes subsequent calculations simpler and reduces the risk of errors. For example, 2/7 is much easier to work with than 10/35.
Q3: How do I convert a fraction to a percentage?
A3: To convert a fraction to a percentage, divide the numerator by the denominator and then multiply the result by 100. Add the "%" symbol to indicate it's a percentage.
Q4: What if I have a more complex scenario, say 17 out of 68?
A4: The same principles apply. You would create the fraction 17/68, find the greatest common divisor (in this case, 17), simplify to 1/4, then convert to a percentage (25%) and a ratio (1:4). The process remains consistent even with larger numbers.
Conclusion: More Than Just a Calculation
"What is 10 of 35?" is not just a simple arithmetic question; it's a gateway to understanding fundamental mathematical concepts. By exploring its representation as a fraction, percentage, and ratio, we've delved into the world of proportions, equivalent fractions, and the practical applications of these concepts in various fields. Mastering these fundamental principles equips you with valuable problem-solving skills applicable throughout life, both in academic and professional settings. Remember, understanding the "why" behind the calculation is just as important as knowing the "how."
Latest Posts
Latest Posts
-
Can A Pca Give Insulin
Sep 01, 2025
-
1 6 Repeating As A Fraction
Sep 01, 2025
-
Demizion Valley Orchard Inc Devleoped
Sep 01, 2025
-
The Higher The Speed The
Sep 01, 2025
-
Biological Evolution Evidence Quick Check
Sep 01, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.