What Is 15 Of 35
cibeltiagestion
Sep 02, 2025 · 6 min read
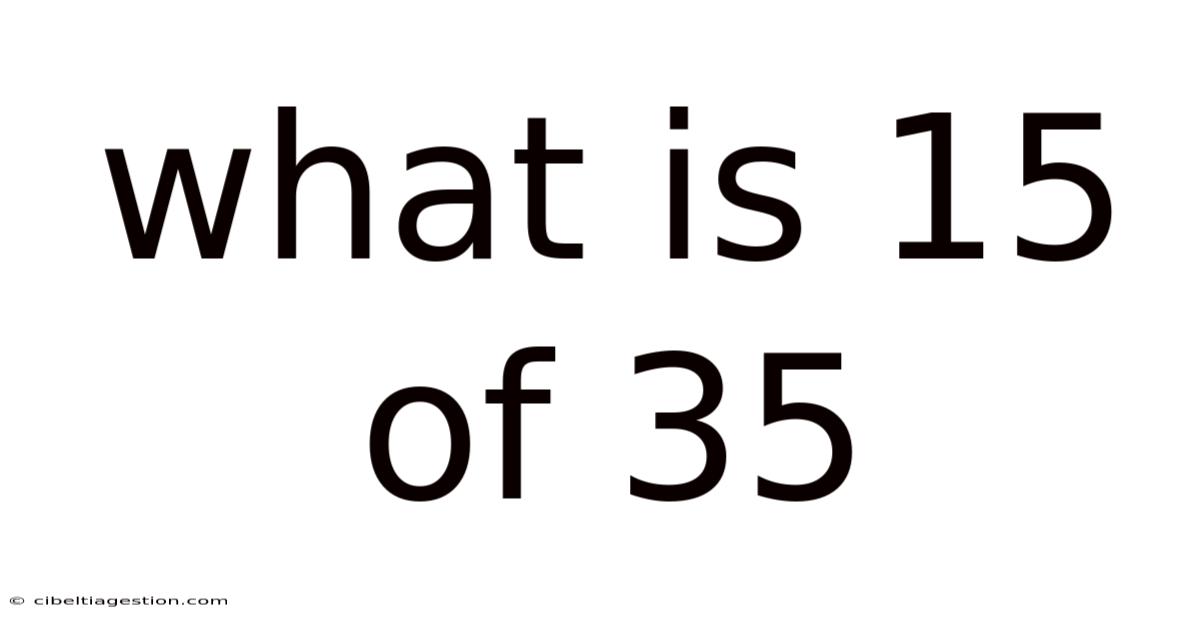
Table of Contents
What is 15 of 35? Unveiling the World of Fractions, Percentages, and Ratios
Understanding fractions, percentages, and ratios is fundamental to everyday life, from splitting bills with friends to calculating discounts at the mall. This comprehensive guide will explore the question "What is 15 of 35?" by delving into various mathematical approaches, providing practical examples, and highlighting the importance of these concepts in diverse contexts. We'll move beyond a simple answer to build a robust understanding of proportional reasoning.
Introduction: Deconstructing the Problem
The question "What is 15 of 35?" inherently implies a relationship between two numbers. It can be interpreted in several ways, each leading to a different but equally valid solution. We'll consider this problem through the lenses of fractions, percentages, and ratios, demonstrating how each approach offers a unique perspective on the relationship between 15 and 35. Mastering these approaches is crucial for success in various academic disciplines and real-world scenarios.
1. The Fractional Approach: Understanding Parts of a Whole
The most straightforward interpretation of "15 of 35" is as a fraction. In this case, 15 represents a portion or part of a larger whole, which is 35. We can express this relationship as a fraction: 15/35.
-
Simplifying the Fraction: The fraction 15/35 can be simplified by finding the greatest common divisor (GCD) of both the numerator (15) and the denominator (35). The GCD of 15 and 35 is 5. Dividing both the numerator and the denominator by 5, we get the simplified fraction: 3/7.
-
Interpreting the Simplified Fraction: The simplified fraction 3/7 means that 15 is 3/7 of 35. This implies that if we divide 35 into 7 equal parts, 15 represents 3 of those parts.
-
Visual Representation: Imagine a pizza cut into 7 equal slices. If you eat 3 slices, you've consumed 3/7 of the pizza. This is analogous to the relationship between 15 and 35, where 15 is 3/7 of 35.
2. The Percentage Approach: Expressing Proportion as a Rate
Another way to interpret "15 of 35" is as a percentage. A percentage represents a proportion out of 100. To express 15/35 as a percentage, we need to convert the fraction to a decimal and then multiply by 100.
-
Converting the Fraction to a Decimal: Divide the numerator (15) by the denominator (35): 15 ÷ 35 ≈ 0.4286
-
Converting the Decimal to a Percentage: Multiply the decimal by 100: 0.4286 × 100 ≈ 42.86%
-
Interpreting the Percentage: This means that 15 represents approximately 42.86% of 35. In other words, 15 is about 42.86 out of every 100 parts of 35.
3. The Ratio Approach: Comparing Two Quantities
The relationship between 15 and 35 can also be expressed as a ratio. A ratio compares the relative sizes of two or more quantities. In this case, the ratio is 15:35.
-
Simplifying the Ratio: Like fractions, ratios can be simplified by dividing both sides by their GCD, which is 5. This simplifies the ratio to 3:7.
-
Interpreting the Ratio: The ratio 3:7 indicates that for every 3 units of one quantity, there are 7 units of another quantity. This is consistent with the fraction and percentage interpretations.
4. Real-World Applications: Putting it all Together
The concepts of fractions, percentages, and ratios are intertwined and frequently applied in everyday situations. Here are some examples illustrating their practical use:
-
Shopping: If a shirt originally costs $35 and is on sale for $15, the discount is 15/35 or 3/7 of the original price, which is approximately 42.86%.
-
Cooking: If a recipe calls for 35 grams of flour and you only have 15 grams, you have only 3/7 (approximately 42.86%) of the required amount.
-
Surveys and Statistics: If 15 out of 35 people surveyed prefer a particular brand, the brand's popularity is represented by the fraction 3/7, the percentage 42.86%, or the ratio 3:7.
5. Expanding Understanding: Proportionality and its Implications
The core concept underlying fractions, percentages, and ratios is proportionality. Proportionality describes a consistent relationship between two or more quantities. In the case of 15 and 35, the relationship is that 15 is consistently 3/7 of 35, regardless of whether we express this relationship as a fraction, percentage, or ratio.
Understanding proportionality is crucial for solving a wide range of problems, including:
- Scaling recipes: If you double a recipe, you must double all ingredients proportionally.
- Map interpretation: Maps use scales to represent distances proportionally.
- Financial calculations: Interest rates, discounts, and taxes all involve proportional calculations.
- Scientific experiments: Data analysis frequently involves establishing and interpreting proportional relationships between variables.
6. Beyond the Basics: Working with More Complex Proportions
While "15 of 35" presents a relatively simple proportional problem, the same principles apply to more complex scenarios. For instance, consider the problem: "If 15 out of 35 students passed an exam, what percentage of students failed?"
To solve this, we would first determine the number of students who failed (35 - 15 = 20). Then, we'd express this as a fraction (20/35), simplify it (4/7), convert it to a decimal (approximately 0.5714), and finally to a percentage (approximately 57.14%). This highlights the versatility of these mathematical tools in tackling various proportional problems.
7. Frequently Asked Questions (FAQ)
-
Q: Is there only one correct answer to "What is 15 of 35"?
A: While the numerical answer is always 3/7, 0.4286, or 42.86% (depending on the format), the interpretation of this answer can vary depending on the context of the problem. Understanding the context is crucial.
-
Q: Why is simplifying fractions and ratios important?
A: Simplifying makes it easier to visualize the relationship between the numbers and compare proportions more effectively. It also reduces computational complexity in more elaborate problems.
-
Q: How can I improve my understanding of fractions, percentages, and ratios?
A: Practice is key! Work through various problems, starting with simple examples and gradually increasing the complexity. Utilize visual aids, such as diagrams and charts, to reinforce your understanding. Consider seeking additional resources like online tutorials or educational websites.
8. Conclusion: Mastering Proportional Reasoning
Understanding "What is 15 of 35?" is more than just solving a simple arithmetic problem. It's about grasping the fundamental concepts of fractions, percentages, and ratios, and applying these tools to analyze and interpret proportional relationships in various contexts. This skill is vital for everyday life, academic success, and professional endeavors. By mastering these concepts, you develop a crucial skillset for navigating a world full of proportional challenges and opportunities. The ability to confidently and accurately handle these calculations empowers you to make informed decisions and effectively solve problems in diverse settings. From budgeting and shopping to scientific analysis and data interpretation, proportional reasoning is an essential tool for success in numerous areas of life.
Latest Posts
Latest Posts
-
How Many Tablespoons Is 2oz
Sep 03, 2025
-
65 67 68 68 70
Sep 03, 2025
-
1ml Is How Many Units
Sep 03, 2025
-
How Long Is A Score
Sep 03, 2025
-
Julia And Katherine Similarities 1984
Sep 03, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.