What Is 15 Of 40
cibeltiagestion
Sep 08, 2025 · 5 min read
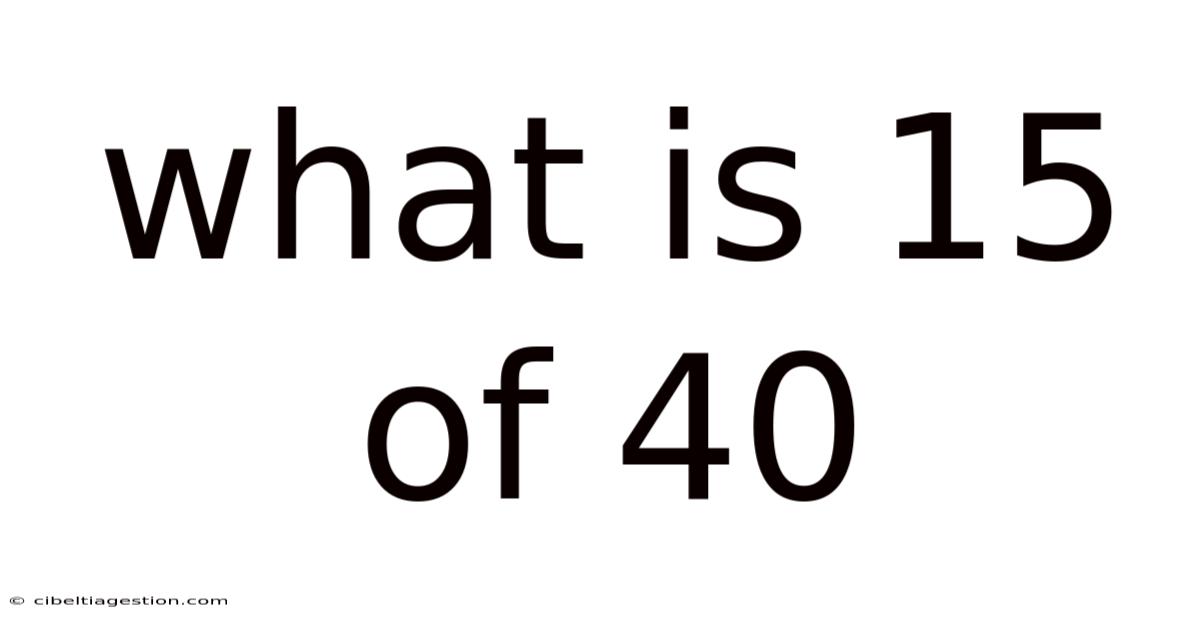
Table of Contents
What is 15 of 40? Unpacking Fractions, Percentages, and Ratios
This article explores the seemingly simple question, "What is 15 of 40?", delving far beyond a simple numerical answer. We'll unpack this question using the frameworks of fractions, percentages, and ratios, illustrating the versatile nature of mathematical concepts and highlighting their practical applications in everyday life. Understanding these concepts is crucial for various fields, from basic accounting and cooking to advanced statistics and engineering. This guide aims to provide a comprehensive understanding for learners of all levels.
Introduction: Understanding the Basics
The question "What is 15 of 40?" inherently involves understanding the relationship between two numbers. It signifies a part-to-whole relationship, where 15 represents a part of a larger whole, which is 40. This relationship can be expressed in various ways, each offering unique insights and applications. We will examine three primary methods: fractions, percentages, and ratios.
1. Representing the Relationship as a Fraction
A fraction represents a part of a whole. In our case, 15 out of 40 can be expressed as the fraction 15/40. This fraction indicates that 15 is the numerator (the part) and 40 is the denominator (the whole).
Simplifying the Fraction: Fractions are often simplified to their lowest terms. This makes them easier to understand and compare. To simplify 15/40, we find the greatest common divisor (GCD) of both the numerator and the denominator. The GCD of 15 and 40 is 5. Dividing both the numerator and the denominator by 5, we get:
15 ÷ 5 / 40 ÷ 5 = 3/8
Therefore, 15 of 40 is equivalent to 3/8. This simplified fraction tells us that 15 represents three-eighths of 40.
2. Converting to a Percentage
Percentages are a convenient way to express fractions as parts of 100. To convert the fraction 3/8 to a percentage, we perform the following calculation:
(3/8) x 100% = 37.5%
Therefore, 15 out of 40 represents 37.5%. This means that 15 constitutes 37.5% of the total 40. This percentage representation is extremely useful in various contexts, from calculating discounts and tax rates to understanding statistical data and performance metrics.
3. Expressing the Relationship as a Ratio
A ratio shows the comparative relationship between two or more quantities. In this case, the ratio of 15 to 40 is written as 15:40 or 15/40. Similar to fractions, ratios can be simplified by dividing both sides by their GCD, which is 5. This simplifies the ratio to:
3:8
The ratio 3:8 indicates that for every 3 units of one quantity, there are 8 units of the other quantity. Ratios are widely used in various fields, including scaling recipes, mixing ingredients, and comparing proportions in scientific experiments.
Real-World Applications: Where This Knowledge Matters
Understanding fractions, percentages, and ratios is not merely an academic exercise; it has numerous practical applications in everyday life. Consider these examples:
-
Shopping: Calculating discounts, sales tax, and comparing unit prices all rely on understanding percentages and ratios. If a product is 25% off, knowing how to calculate the actual price saved is essential.
-
Cooking: Recipes often require adjusting ingredient quantities based on the number of servings. Understanding ratios allows you to accurately scale recipes up or down. For example, if a recipe calls for a 1:2 ratio of flour to sugar, you can easily adjust the quantities to suit your needs.
-
Finance: Calculating interest rates, loan repayments, and investment returns involves a deep understanding of percentages and ratios. Understanding these concepts is crucial for making informed financial decisions.
-
Data Analysis: Interpreting data from surveys, polls, and scientific studies requires proficiency in calculating percentages and ratios to understand trends and make informed conclusions.
-
Construction and Engineering: Scaling blueprints, calculating material quantities, and determining proportions in various structures rely heavily on the principles of ratios and percentages.
Further Exploration: Expanding Your Understanding
Beyond the basic calculations, let’s explore some related concepts that deepen our understanding of the relationship between 15 and 40.
-
Proportions: A proportion is a statement of equality between two ratios. For example, the proportion 15/40 = 3/8 indicates that the ratios 15:40 and 3:8 are equal. Understanding proportions allows us to solve for unknown quantities in various problems.
-
Decimal Representation: The fraction 3/8 can also be expressed as a decimal: 0.375. This decimal representation provides another way to represent the part-to-whole relationship between 15 and 40.
-
Visual Representations: Using diagrams like pie charts or bar graphs can help visualize the relationship between 15 and 40, making it easier to comprehend. A pie chart divided into 8 equal slices, with 3 slices representing 15 and the remaining 5 slices representing the remaining 25, provides a clear visual illustration of the fraction 3/8.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to find 15 of 40? A: Yes, you can use a calculator to divide 15 by 40, which will give you the decimal representation 0.375. You can then multiply this by 100 to get the percentage (37.5%).
-
Q: Why is simplifying fractions important? A: Simplifying fractions makes them easier to understand, compare, and use in further calculations. It reduces the complexity of the numbers while maintaining their proportional relationship.
-
Q: Are ratios and fractions the same? A: While ratios and fractions are closely related and often used interchangeably, there is a subtle difference. Fractions always represent a part of a whole, while ratios can compare any two quantities, not necessarily a part to a whole.
-
Q: What are some common uses of percentages in daily life? A: Percentages are used extensively in sales (discounts), finance (interest rates), statistics (data representation), and many other areas.
Conclusion: Mastering the Fundamentals
The seemingly simple question, "What is 15 of 40?", opens a window into the world of fractions, percentages, and ratios – fundamental mathematical concepts with widespread applications in everyday life. Understanding these concepts, from simplifying fractions to converting them into percentages and ratios, empowers us to solve problems efficiently and make informed decisions in various contexts. Mastering these core mathematical skills is crucial for academic success and navigating the complexities of the real world. By grasping these fundamental concepts, you build a strong foundation for tackling more advanced mathematical challenges and confidently applying these skills in your daily life. Continue practicing, exploring different applications, and you'll find yourself increasingly comfortable with these essential mathematical tools.
Latest Posts
Latest Posts
-
How Many 1 2 Is 3 4
Sep 09, 2025
-
Lewis Dot Structure For Rbf
Sep 09, 2025
-
What Is 70 Of 35
Sep 09, 2025
-
Equity Theory Looks At How
Sep 09, 2025
-
What Is 25 Of 380
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.