What Is 15 Of 50
cibeltiagestion
Sep 13, 2025 · 5 min read
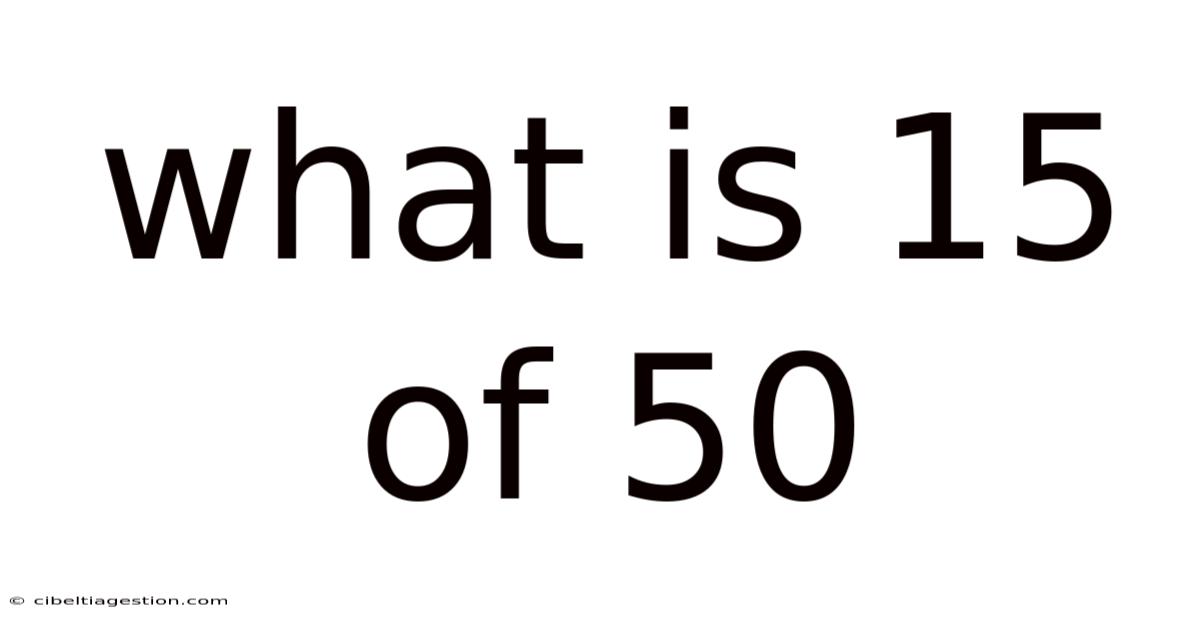
Table of Contents
What is 15 of 50? Unpacking Percentages, Fractions, and Ratios
Finding out "what is 15 of 50?" might seem like a simple question, but it opens the door to understanding fundamental mathematical concepts that are crucial in various aspects of life, from calculating discounts to comprehending complex data analysis. This article will not just answer the question directly but will also delve deeper into the underlying principles of percentages, fractions, and ratios, offering a comprehensive understanding of how to tackle similar problems. We will explore different methods of calculation, providing clarity and building a strong foundation in mathematical reasoning.
Understanding the Question: Fractions, Percentages, and Ratios
The question "What is 15 of 50?" essentially asks us to determine the relationship between 15 and 50. This relationship can be expressed in several ways:
- As a fraction: 15 out of 50 can be written as the fraction 15/50.
- As a percentage: It represents a certain percentage of 50.
- As a ratio: The ratio of 15 to 50 can be expressed as 15:50.
Understanding these three representations is crucial for solving the problem and understanding similar calculations. Each offers a slightly different perspective on the same underlying relationship.
Method 1: Calculating the Fraction and Simplifying
The most straightforward approach is to express the relationship as a fraction: 15/50. This fraction represents 15 parts out of a total of 50 parts. To simplify this fraction, we find the greatest common divisor (GCD) of 15 and 50. The GCD of 15 and 50 is 5. Dividing both the numerator (15) and the denominator (50) by 5, we get:
15/50 = (15 ÷ 5) / (50 ÷ 5) = 3/10
Therefore, 15 is 3/10 of 50.
Method 2: Converting the Fraction to a Percentage
The fraction 3/10 can easily be converted to a percentage. To do this, we multiply the fraction by 100%:
(3/10) * 100% = 30%
Therefore, 15 is 30% of 50.
Method 3: Using Proportions
We can also solve this problem using proportions. We can set up a proportion to find the percentage:
15/50 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', we cross-multiply:
50x = 1500
x = 1500/50
x = 30
Therefore, 15 is 30% of 50. This method clearly demonstrates the relationship between the parts and the whole.
Method 4: Decimal Representation
The fraction 3/10 can also be expressed as a decimal: 0.3. This decimal represents 3 tenths, which is equivalent to 30%. This approach is particularly useful when working with calculations involving decimals.
Real-World Applications: Understanding the Significance
Understanding the relationship between 15 and 50, expressed as a fraction, percentage, or ratio, has practical applications in many areas:
- Discount Calculations: Imagine a $50 item is discounted by $15. This represents a 30% discount.
- Test Scores: If you answered 15 questions correctly out of 50, your score is 30%.
- Data Analysis: In statistical analysis, understanding proportions and percentages is crucial for interpreting data and drawing meaningful conclusions. For instance, if a survey of 50 people shows 15 prefer a certain product, this indicates a 30% preference rate.
- Financial Calculations: From calculating interest rates to understanding investment returns, the ability to work with fractions, percentages, and ratios is fundamental.
Expanding the Concept: Working with Different Numbers
The methods outlined above can be applied to any similar problem. Let's consider a slightly more complex example: What is 27 out of 75?
- Fraction: 27/75
- Simplifying the Fraction: The GCD of 27 and 75 is 3. Therefore, 27/75 simplifies to 9/25.
- Percentage: (9/25) * 100% = 36%
- Proportion: 27/75 = x/100; Solving for x gives x = 36.
Therefore, 27 is 36% of 75. This demonstrates the versatility and applicability of these mathematical concepts.
Frequently Asked Questions (FAQ)
Q1: What if the numbers are larger or have no common factors?
A1: Even with larger numbers or those lacking common factors, the principles remain the same. You would still express the relationship as a fraction, simplify if possible, and then convert it to a percentage using the methods described above. Calculators can be extremely helpful in simplifying fractions and performing the calculations.
Q2: How do I calculate the percentage of a number?
A2: To calculate a percentage of a number, you simply multiply the percentage (expressed as a decimal) by the number. For example, 30% of 50 is 0.30 * 50 = 15.
Q3: What is the difference between a fraction, a percentage, and a ratio?
A3: While all three represent relationships between two numbers, they differ in their expression:
- Fraction: Expresses a part of a whole using a numerator and denominator (e.g., 3/10).
- Percentage: Expresses a fraction as a part of 100 (e.g., 30%).
- Ratio: Expresses a relationship between two quantities (e.g., 3:10). It doesn't necessarily represent a part of a whole.
Q4: How can I improve my understanding of percentages and fractions?
A4: Practice is key! Work through various problems, starting with simpler examples and gradually increasing the complexity. You can find many online resources, worksheets, and practice problems to help you build your skills. Visual aids, such as diagrams and charts, can also significantly improve your understanding of these concepts.
Conclusion: Mastering Fundamental Mathematical Concepts
The question "What is 15 of 50?" is a gateway to understanding fundamental mathematical concepts like fractions, percentages, and ratios. These concepts are not just abstract mathematical ideas; they are essential tools applicable in numerous aspects of daily life, from personal finance and shopping to scientific analysis and data interpretation. By mastering these fundamental concepts, you are building a solid foundation for more advanced mathematical studies and problem-solving in various fields. Remember that practice is key to solidifying your understanding and building confidence in tackling similar problems in the future. Don't hesitate to explore different methods and approaches until you find the ones that work best for you.
Latest Posts
Latest Posts
-
What Is Equal To 2 6
Sep 13, 2025
-
Check Returned Refer To Maker
Sep 13, 2025
-
According To Sociologists Doctors Are
Sep 13, 2025
-
Multiplier For 10 Degree Offset
Sep 13, 2025
-
Hybridization Of Br In Bro
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.