What Is 150 Of 42
cibeltiagestion
Sep 07, 2025 · 6 min read
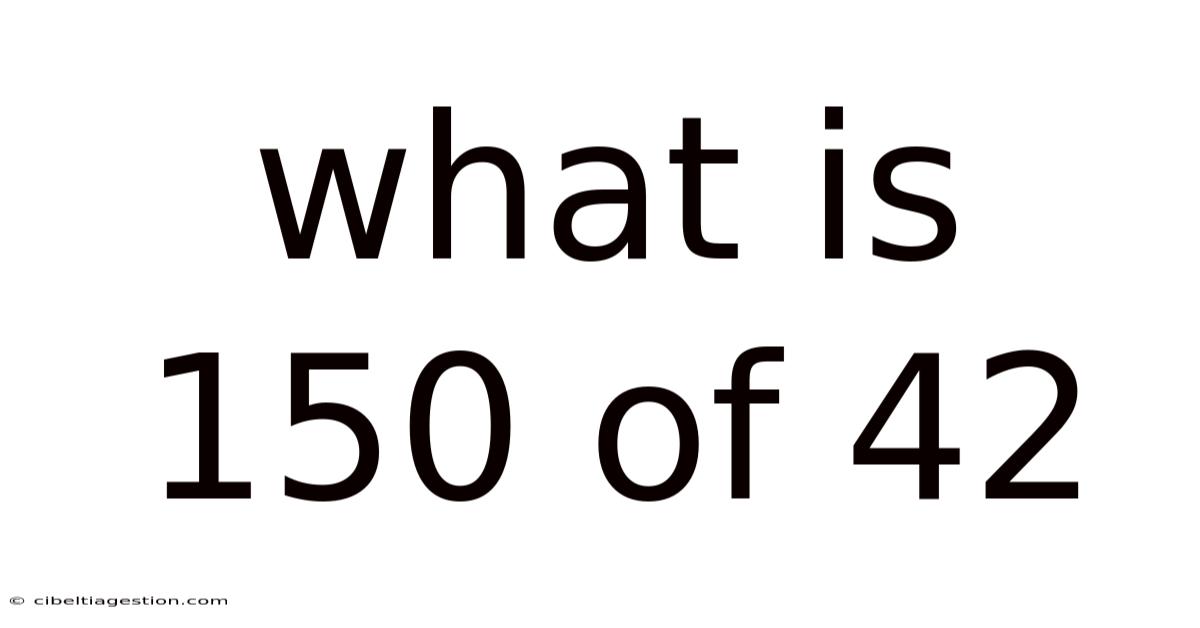
Table of Contents
Decoding 150% of 42: A Deep Dive into Percentages and their Applications
What is 150% of 42? This seemingly simple question opens the door to a broader understanding of percentages, a fundamental concept in mathematics with widespread applications in everyday life, from calculating discounts and taxes to understanding statistical data and financial growth. This article will not only answer this specific question but also delve into the underlying principles, explore different methods of calculation, and examine the real-world relevance of percentage calculations.
Understanding Percentages: The Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ( per cent). Therefore, 150% means 150 out of 100, or 1.5 as a decimal. This understanding forms the bedrock for calculating any percentage of a given number.
Calculating 150% of 42: Method 1 - The Decimal Approach
The most straightforward method involves converting the percentage to a decimal and then multiplying it by the number.
-
Convert the percentage to a decimal: 150% is equivalent to 150/100 = 1.5
-
Multiply the decimal by the number: 1.5 * 42 = 63
Therefore, 150% of 42 is 63.
Calculating 150% of 42: Method 2 - The Fraction Approach
Alternatively, we can use fractions.
-
Express the percentage as a fraction: 150% can be written as 150/100, which simplifies to 3/2.
-
Multiply the fraction by the number: (3/2) * 42 = (3 * 42) / 2 = 126 / 2 = 63
Again, we arrive at the answer: 150% of 42 is 63.
Beyond the Calculation: Understanding the Concept of "More Than 100%"
It's crucial to grasp the significance of percentages exceeding 100%. While percentages between 0% and 100% represent portions of a whole, percentages above 100% indicate a quantity greater than the original whole. In our example, 150% of 42 signifies a quantity that is 150% of 42, meaning it's 50% larger than 42 itself. This concept is frequently encountered in various contexts.
For instance, if a company experiences a 150% increase in profits, it means its profits have grown by 1.5 times their original value. Similarly, if a population increases by 150%, it's expanded to 250% of its initial size (100% + 150% = 250%).
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous, finding their way into numerous aspects of our daily lives:
-
Finance: Calculating interest rates, loan repayments, profit margins, investment returns, and tax deductions all rely heavily on percentage calculations. Understanding percentages is crucial for informed financial decision-making.
-
Retail: Discounts, sales tax, and markups are all expressed as percentages. Consumers need to be comfortable with percentage calculations to assess the actual price of goods after discounts or the final cost including tax.
-
Science: Percentage changes are used extensively to represent variations in scientific measurements, experimental results, and statistical data. For example, the percentage change in temperature, the percentage error in an experiment, or the percentage of a population with a certain characteristic.
-
Health and Nutrition: Nutritional labels often list the percentage of daily recommended intake for various nutrients. This information allows consumers to make informed choices about their diet.
-
Education: Grade calculations, performance evaluations, and test scores are often expressed as percentages, offering a standardized way to assess progress and achievement.
Different Ways to Express Percentages
It's important to remember that percentages can be expressed in several ways:
-
Decimal: As seen in our first method, 150% is equivalent to 1.5.
-
Fraction: 150% can also be represented as 3/2, which helps visualize the relationship between the parts and the whole.
-
Ratio: 150% can be expressed as a ratio of 150:100, simplifying to 3:2.
Understanding these different representations adds flexibility and enhances comprehension of the concept.
Solving More Complex Percentage Problems
The principles discussed here extend to more complex percentage problems. For instance, calculating the percentage increase or decrease between two numbers requires a slightly different approach but still relies on the fundamental understanding of percentages. Similarly, finding the original value when a percentage is applied involves reverse calculation.
Example 1: Percentage Increase
Let's say a company's profit increased from $40,000 to $60,000. To calculate the percentage increase:
-
Find the difference: $60,000 - $40,000 = $20,000
-
Divide the difference by the original value: $20,000 / $40,000 = 0.5
-
Multiply by 100 to express as a percentage: 0.5 * 100 = 50%
Therefore, the company's profit increased by 50%.
Example 2: Percentage Decrease
If the company's profit decreased from $60,000 to $48,000:
-
Find the difference: $60,000 - $48,000 = $12,000
-
Divide the difference by the original value: $12,000 / $60,000 = 0.2
-
Multiply by 100 to express as a percentage: 0.2 * 100 = 20%
Therefore, the company's profit decreased by 20%.
Example 3: Finding the Original Value
If a discounted price of $30 is 80% of the original price, we can find the original price:
-
Convert the percentage to a decimal: 80% = 0.8
-
Divide the discounted price by the decimal: $30 / 0.8 = $37.50
The original price was $37.50.
Frequently Asked Questions (FAQ)
Q: What if I need to calculate more than 100%?
A: Calculating percentages greater than 100% follows the same principles. Simply convert the percentage to a decimal (e.g., 125% = 1.25) and multiply by the number. This represents an increase beyond the original value.
Q: How can I calculate percentages on a calculator?
A: Most calculators have a percentage button (%). To calculate 150% of 42, you would enter 42, then multiply by 150, then press the "%" button. The result will be 63. Alternatively, you can simply multiply 42 by 1.5.
Q: Are there any online tools to help with percentage calculations?
A: Yes, many websites and online calculators are dedicated to percentage calculations. These tools can be particularly useful for more complex percentage problems.
Q: Why are percentages so important?
A: Percentages provide a standardized and easily understandable way to compare quantities, proportions, and changes. Their widespread use stems from their simplicity and clarity in conveying relative values.
Conclusion
Calculating 150% of 42, which equals 63, is a fundamental step in understanding percentages. However, the true value of this knowledge extends far beyond this single calculation. A comprehensive grasp of percentages is an essential skill for navigating the complexities of everyday life, from managing finances to interpreting data and making informed decisions across numerous domains. Mastering percentage calculations empowers you with a versatile tool for understanding and analyzing the numerical world around you. The examples and explanations provided in this article aim to equip you with not only the ability to solve percentage problems but also a deeper conceptual understanding of this crucial mathematical concept.
Latest Posts
Latest Posts
-
Use Pious In A Sentence
Sep 07, 2025
-
Which Figures Demonstrate A Reflection
Sep 07, 2025
-
The Suns Observed Spectrum Is
Sep 07, 2025
-
What Is 40 Of 225
Sep 07, 2025
-
I Eat Apples In Spanish
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about What Is 150 Of 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.