What Is 2/5 Equal To
cibeltiagestion
Sep 17, 2025 · 6 min read
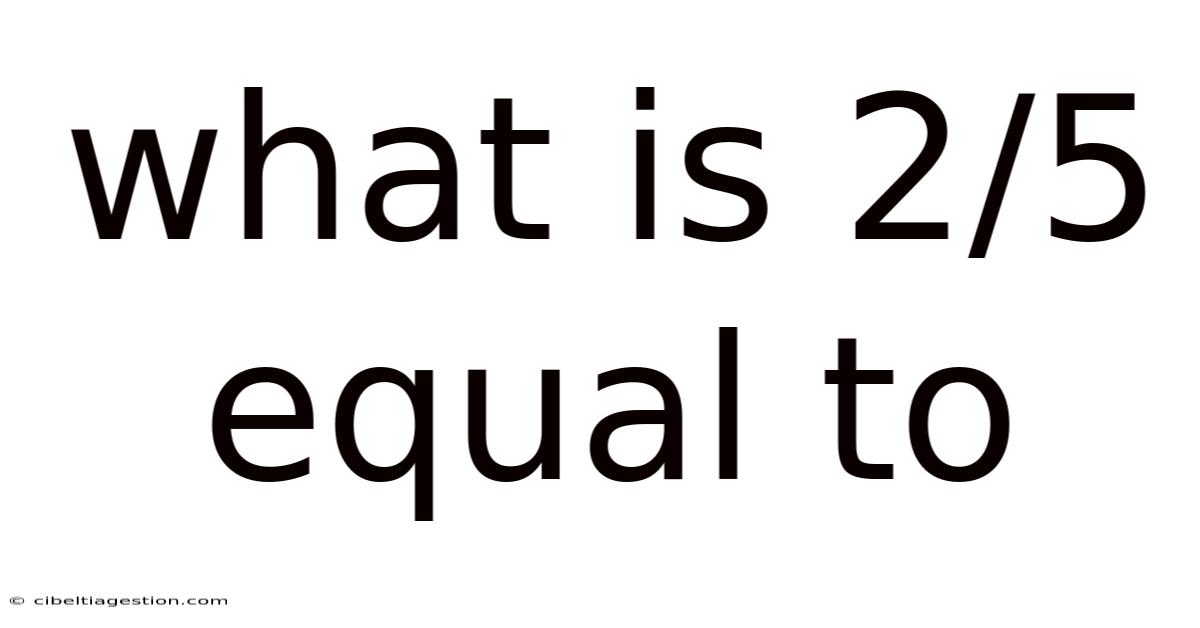
Table of Contents
What is 2/5 Equal To? Unpacking Fractions and Their Equivalents
The seemingly simple question, "What is 2/5 equal to?", opens a door to a vast world of mathematical concepts. This article delves deep into understanding fractions, exploring different ways to represent 2/5, explaining the underlying principles, and providing practical applications. We'll move beyond simply stating the answer and equip you with a solid grasp of fractional equivalence.
Understanding Fractions: The Building Blocks
Before we dive into the specifics of 2/5, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
In the fraction 2/5, 2 is the numerator and 5 is the denominator. This means we have 2 parts out of a total of 5 equal parts. Imagine a pizza cut into 5 equal slices; 2/5 represents having 2 of those slices.
Representing 2/5: Different Forms, Same Value
While 2/5 is a perfectly valid representation, we can express the same quantity in other forms. These different representations are called equivalent fractions. The core concept is that the ratio between the numerator and denominator remains the same, even if the numbers change.
1. Decimal Representation:
To convert a fraction to a decimal, we simply divide the numerator by the denominator. In this case:
2 ÷ 5 = 0.4
Therefore, 2/5 is equal to 0.4.
2. Percentage Representation:
A percentage represents a fraction out of 100. To convert a fraction to a percentage, we first convert it to a decimal and then multiply by 100%.
0.4 x 100% = 40%
So, 2/5 is also equal to 40%.
3. Equivalent Fractions:
We can create equivalent fractions by multiplying both the numerator and the denominator by the same number (except zero). This doesn't change the overall value of the fraction because we're essentially multiplying by 1 (any number divided by itself equals 1).
For example:
- Multiplying both numerator and denominator by 2: (2 x 2) / (5 x 2) = 4/10
- Multiplying both numerator and denominator by 3: (2 x 3) / (5 x 3) = 6/15
- Multiplying both numerator and denominator by 4: (2 x 4) / (5 x 4) = 8/20
All of these fractions – 4/10, 6/15, 8/20, etc. – are equivalent to 2/5. They all represent the same proportion of a whole.
Simplifying Fractions: Finding the Simplest Form
Sometimes, fractions can be simplified to their lowest terms. This means reducing the numerator and denominator to their smallest possible whole numbers while maintaining the same value. This is done by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
In the case of 2/5, the GCD of 2 and 5 is 1. Since dividing both by 1 doesn't change the numbers, 2/5 is already in its simplest form.
However, let's consider the equivalent fraction 4/10. The GCD of 4 and 10 is 2. Dividing both by 2 gives us 2/5, confirming that 4/10 simplifies to 2/5.
Visualizing Fractions: A Concrete Understanding
Visual aids can greatly enhance our understanding of fractions. Let's visualize 2/5 using different examples:
-
A Circle: Imagine a circle divided into 5 equal segments. Shading 2 of those segments represents 2/5.
-
A Rectangle: A rectangle divided into 5 equal columns. Shading 2 of those columns visually demonstrates 2/5.
-
A Number Line: Mark a number line from 0 to 1. Divide the space between 0 and 1 into 5 equal parts. The second mark from 0 represents 2/5.
Practical Applications of 2/5 and Fractional Equivalence
Understanding fractions and their equivalents is crucial in many aspects of life:
-
Cooking: Recipes often use fractions to specify ingredient amounts (e.g., 2/5 cup of flour).
-
Measurement: Measuring lengths, weights, and volumes often involves fractions (e.g., 2/5 of a meter).
-
Finance: Calculating percentages, discounts, and interest rates heavily relies on fractional concepts.
-
Data Analysis: Representing proportions and probabilities in data analysis frequently uses fractions and percentages.
-
Geometry: Understanding areas and proportions of shapes often requires working with fractions.
Advanced Concepts: Operations with Fractions
Once we understand the basics of fractions, we can perform various operations like addition, subtraction, multiplication, and division. For instance:
-
Adding Fractions: To add fractions with the same denominator, we add the numerators and keep the denominator the same. For example, 2/5 + 1/5 = 3/5. Adding fractions with different denominators requires finding a common denominator first.
-
Subtracting Fractions: Similar to addition, subtracting fractions with the same denominator involves subtracting the numerators while keeping the denominator the same.
-
Multiplying Fractions: To multiply fractions, multiply the numerators together and multiply the denominators together. For example, (2/5) x (1/2) = 2/10 = 1/5.
-
Dividing Fractions: To divide fractions, we invert the second fraction (reciprocal) and then multiply. For example, (2/5) ÷ (1/2) = (2/5) x (2/1) = 4/5.
Frequently Asked Questions (FAQ)
Q1: Can 2/5 be expressed as a mixed number?
A1: No. A mixed number is a whole number combined with a proper fraction (numerator smaller than the denominator). Since 2/5 is a proper fraction, it cannot be expressed as a mixed number.
Q2: What is the reciprocal of 2/5?
A2: The reciprocal of a fraction is obtained by switching the numerator and the denominator. The reciprocal of 2/5 is 5/2.
Q3: How do I compare 2/5 and other fractions?
A3: To compare fractions, you can convert them to decimals or find a common denominator. For example, to compare 2/5 and 3/7, convert them to decimals (0.4 and 0.428...) or find a common denominator (35), resulting in 14/35 and 15/35, showing that 3/7 is greater than 2/5.
Q4: Are there any real-world examples where 2/5 is significant?
A4: Yes, many! For example, in some countries, a 40% discount (equivalent to 2/5) is a common sales promotion. In various manufacturing processes, 2/5 might represent a specific ratio of ingredients or a proportion of a task completed.
Conclusion: Mastering Fractions, One Step at a Time
The seemingly straightforward question "What is 2/5 equal to?" has led us on a journey through the fascinating world of fractions. We've explored different representations, equivalent fractions, simplification, visualization techniques, and practical applications. Remember, understanding fractions is a foundational skill with far-reaching implications across various fields. By grasping the core concepts, you'll not only answer simple questions but also build a strong mathematical foundation for tackling more complex problems in the future. The ability to manipulate and understand fractions unlocks a deeper understanding of the world around us and empowers you to solve problems effectively in numerous contexts.
Latest Posts
Latest Posts
-
Transforma Los Adjetivos En Adverbios
Sep 17, 2025
-
10 Times As Much As
Sep 17, 2025
-
X 2 2x 17 0
Sep 17, 2025
-
1 8 Tsp 1 8 Tsp
Sep 17, 2025
-
1 83 Repeating As A Fraction
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/5 Equal To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.