What Is 20 Of 85
cibeltiagestion
Sep 10, 2025 · 5 min read
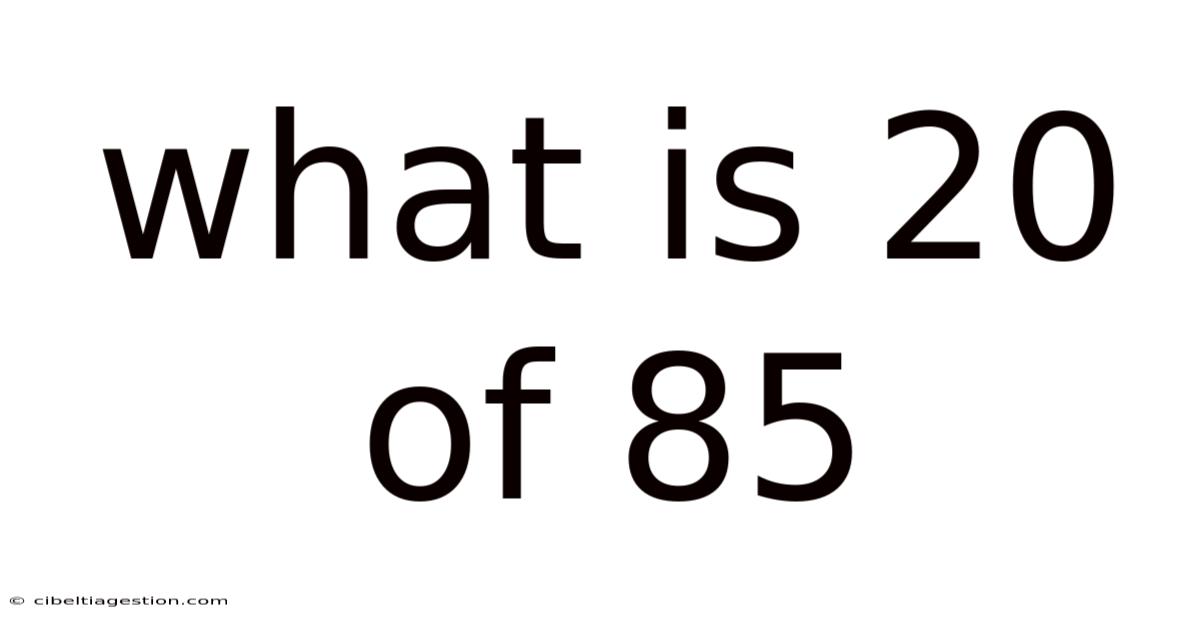
Table of Contents
What is 20% of 85? A Deep Dive into Percentages and Their Applications
Finding 20% of 85 might seem like a simple calculation, but it opens a door to understanding a fundamental concept in mathematics with widespread applications in everyday life, from calculating discounts to understanding financial reports. This article will not only answer the question directly but will also explore the underlying principles of percentages, different methods of calculation, and real-world examples to solidify your understanding.
Understanding Percentages
A percentage is simply a fraction expressed as a part of 100. The word "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, 20% means 20 out of 100, or 20/100, which simplifies to 1/5. This fractional representation is key to understanding how to calculate percentages.
Calculating 20% of 85: Three Methods
There are several ways to calculate 20% of 85. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. First, convert the percentage to a decimal by dividing it by 100. 20% divided by 100 is 0.20 (or simply 0.2). Then, multiply this decimal by the number you're finding the percentage of:
85 x 0.2 = 17
Therefore, 20% of 85 is 17.
Method 2: Using Fractions
As mentioned earlier, 20% is equivalent to the fraction 1/5. To find 20% of 85 using this method, we multiply 85 by 1/5:
85 x (1/5) = 85/5 = 17
Again, we arrive at the answer: 17. This method is particularly useful when dealing with simpler percentages that have easy fractional equivalents, like 25% (1/4), 50% (1/2), or 75% (3/4).
Method 3: Proportion Method
This method involves setting up a proportion. We know that 20 is to 100 as x is to 85. This can be written as:
20/100 = x/85
To solve for x, we cross-multiply:
20 * 85 = 100 * x
1700 = 100x
x = 1700/100 = 17
This confirms once more that 20% of 85 is 17. While this method might seem more complex for this specific problem, it’s a valuable approach for solving more complex percentage problems.
Real-World Applications of Percentage Calculations
Understanding how to calculate percentages is crucial in numerous real-world scenarios:
-
Shopping Discounts: Sales often advertise discounts as percentages. For example, a 20% discount on an $85 item would mean a saving of $17 (as we've just calculated), resulting in a final price of $68.
-
Taxes and Tips: Calculating sales tax or adding a tip to a restaurant bill involves percentage calculations. If the sales tax is 6%, you would calculate 6% of the total bill amount. Similarly, a 15% tip would be calculated on the pre-tax amount.
-
Financial Analysis: Percentage changes are used extensively in financial reports to track growth or decline in various metrics like revenue, profits, and stock prices. For instance, a 10% increase in revenue means that the revenue has grown by 10% of its previous value.
-
Statistics and Data Analysis: Percentages are essential for presenting and interpreting data. For example, a survey might report that 70% of respondents prefer a particular product. This allows for easy comprehension and comparison of data.
-
Scientific Calculations and Measurements: Percentages are used in various scientific fields, including chemistry (concentration of solutions), physics (efficiency of machines), and biology (population growth).
Expanding on Percentage Concepts: Beyond the Basics
While finding 20% of 85 is a simple calculation, it's beneficial to expand our understanding of percentages further:
-
Calculating the Percentage Increase or Decrease: To find the percentage increase or decrease between two numbers, follow these steps:
- Find the difference: Subtract the smaller number from the larger number.
- Divide by the original number: Divide the difference by the original (starting) number.
- Multiply by 100: Multiply the result by 100 to express it as a percentage.
For example, if a price increases from $50 to $60, the percentage increase is:
(60-50)/50 * 100 = 20%
-
Finding the Original Number: If you know the percentage and the resulting amount, you can find the original number. Let's say you received a 20% discount and paid $68. To find the original price:
- Calculate the remaining percentage: Since you received a 20% discount, you paid 100% - 20% = 80% of the original price.
- Set up a proportion: 80/100 = 68/x
- Solve for x: x = (68 * 100) / 80 = 85. The original price was $85.
-
Compounding Percentages: When dealing with consecutive percentage changes, the calculations become more complex due to compounding. For example, a 10% increase followed by a 10% decrease does not result in the original value; instead, it results in a slight decrease due to the compounding effect.
Frequently Asked Questions (FAQ)
Q: What if I need to calculate a percentage that doesn't have an easy fraction equivalent, like 17%?
A: You can still use the decimal method. Convert 17% to 0.17 and multiply it by the number.
Q: Are there any shortcuts for calculating common percentages?
A: Yes! Memorizing the decimal equivalents for common percentages (like 10%, 25%, 50%, 75%) can speed up calculations.
Q: What if I'm working with very large numbers or need to calculate percentages frequently?
A: Spreadsheets and calculators can significantly simplify percentage calculations, especially for large datasets or complex problems.
Conclusion
This article not only provided the solution to "What is 20% of 85?" (17) but also delved into the fundamental principles of percentages, explored various calculation methods, and highlighted their importance in numerous real-world applications. Mastering percentage calculations is a valuable skill with wide-ranging benefits across various fields. By understanding the concepts discussed here, you're well-equipped to handle a broader range of percentage-related problems and to apply this knowledge effectively in your daily life and professional endeavors. Remember, the key is to understand the underlying principles and choose the calculation method that best suits your needs.
Latest Posts
Latest Posts
-
How Many Cups Is 3oz
Sep 10, 2025
-
69 Degrees Celsius To Fahrenheit
Sep 10, 2025
-
Convert 77 Kilos To Pounds
Sep 10, 2025
-
They Will See In Spanish
Sep 10, 2025
-
1 3 Of 3 Feet
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 85 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.