What Is 25 Of 250
cibeltiagestion
Sep 06, 2025 · 5 min read
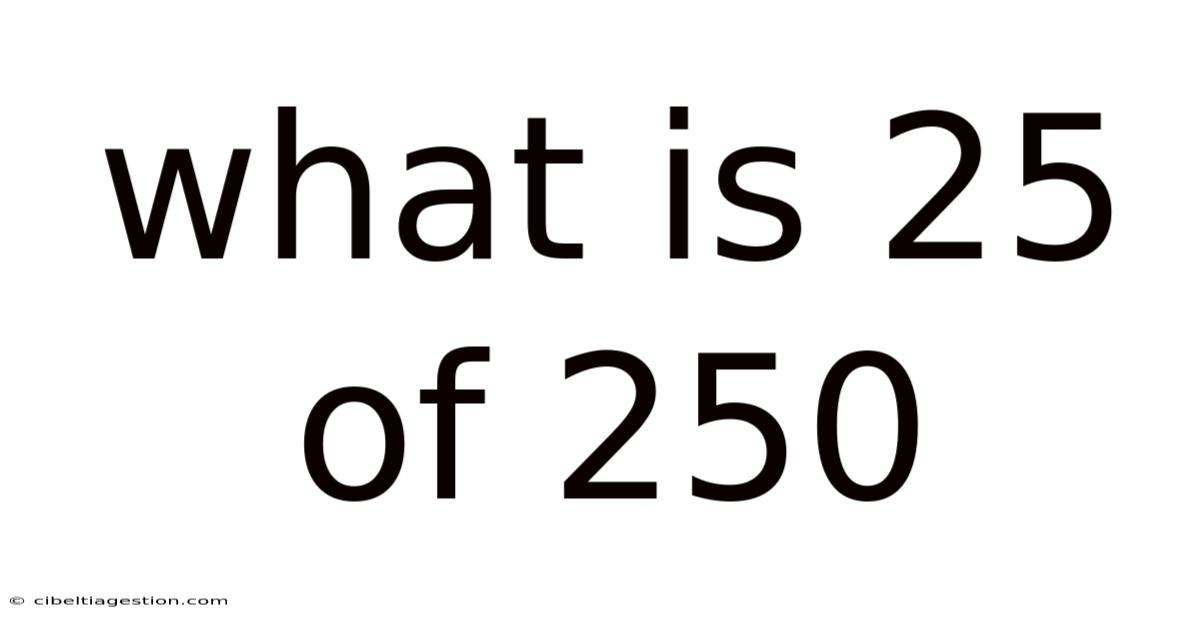
Table of Contents
What is 25 of 250? Understanding Fractions, Percentages, and Ratios
This article explores the seemingly simple question, "What is 25 of 250?" It's more than just a basic arithmetic problem; it's a gateway to understanding fundamental mathematical concepts like fractions, percentages, and ratios. We'll break down the calculation in various ways, explore the underlying principles, and delve into real-world applications to ensure a comprehensive understanding.
Understanding the Problem
The phrase "25 of 250" implies a part-to-whole relationship. We're interested in determining what proportion 25 represents when compared to the total quantity of 250. This can be expressed in several ways: as a fraction, a percentage, or a ratio.
Method 1: Expressing as a Fraction
The most straightforward approach is to represent the relationship as a fraction. The part (25) becomes the numerator, and the whole (250) becomes the denominator:
25/250
This fraction can be simplified by finding the greatest common divisor (GCD) of 25 and 250. The GCD of 25 and 250 is 25. Dividing both the numerator and the denominator by 25 gives us:
25 ÷ 25 / 250 ÷ 25 = 1/10
Therefore, 25 is one-tenth (1/10) of 250.
Method 2: Converting to a Percentage
Percentages are a common way to express proportions. To convert the fraction 1/10 to a percentage, we multiply it by 100%:
(1/10) * 100% = 10%
So, 25 is 10% of 250.
Method 3: Expressing as a Ratio
A ratio expresses the relationship between two quantities. In this case, the ratio of 25 to 250 can be written as:
25:250
Similar to the fraction, we can simplify this ratio by dividing both numbers by their GCD (25):
25 ÷ 25 : 250 ÷ 25 = 1:10
This simplified ratio, 1:10, indicates that for every one unit of the part, there are ten units of the whole.
Real-World Applications
Understanding how to calculate the proportion of one number to another has countless practical applications:
-
Sales and Discounts: If a store offers a discount of 25 dollars on an item priced at 250 dollars, the discount represents 10% of the original price.
-
Surveys and Statistics: If 25 out of 250 respondents answered "yes" to a survey question, 10% of the respondents gave a positive response.
-
Financial Analysis: In finance, understanding proportions is crucial for calculating returns on investment, analyzing financial statements, and evaluating risk. For example, if you invested 25 dollars out of a total investment of 250 dollars in a particular stock, that represents a 10% allocation to that stock.
-
Recipe Scaling: If a recipe calls for 25 grams of flour as part of a 250-gram total, you can easily scale the recipe up or down by maintaining the 1:10 ratio.
-
Scientific Measurements: In scientific experiments, ratios and percentages are used to express concentrations, yields, and other important quantitative relationships.
Expanding the Understanding: Proportions and Equations
The problem of "25 of 250" can also be approached using the concept of proportions. A proportion is a statement that two ratios are equal. We can set up a proportion to solve for an unknown value:
25/250 = x/100
Where 'x' represents the percentage. To solve for x, we cross-multiply:
25 * 100 = 250 * x
2500 = 250x
x = 2500/250
x = 10
This confirms that 25 is 10% of 250.
Delving Deeper: Percentage Increase and Decrease
Building upon this foundational understanding, let's explore how to calculate percentage increases and decreases. Imagine the scenario changes: The initial value is 250, and it increases to 275. What's the percentage increase?
- Calculate the difference: 275 - 250 = 25
- Divide the difference by the original value: 25 / 250 = 0.1
- Multiply by 100% to express as a percentage: 0.1 * 100% = 10%
The value increased by 10%.
Conversely, if the value decreased from 250 to 225:
- Calculate the difference: 250 - 225 = 25
- Divide the difference by the original value: 25 / 250 = 0.1
- Multiply by 100% to express as a percentage: 0.1 * 100% = 10%
The value decreased by 10%.
Advanced Concepts: Applications in Algebra
Understanding fractions and percentages forms the bedrock for solving more complex algebraic problems. For example, consider the following word problem:
"A store is having a sale, offering a 20% discount on all items. If a customer purchases an item with a final price of $200 after the discount, what was the original price?"
This problem requires working backward from the discounted price to find the original price. We can set up an equation:
Original Price - (20% of Original Price) = $200
Let 'x' represent the original price:
x - 0.20x = 200
0.80x = 200
x = 200 / 0.80
x = $250
The original price of the item was $250.
Frequently Asked Questions (FAQ)
Q: What if the numbers aren't easily divisible?
A: If the numbers don't have a readily apparent GCD, you can use a calculator or long division to simplify the fraction or ratio. Alternatively, you can leave the fraction in its unsimplified form, which still accurately represents the proportion.
Q: Can I use a calculator to solve this?
A: Absolutely! A calculator can simplify the process of division and conversion to percentages.
Q: Are there different ways to represent this proportion?
A: Yes, as demonstrated, the proportion can be expressed as a fraction, percentage, ratio, or using a proportion equation. The most appropriate method often depends on the context of the problem.
Conclusion
The seemingly simple question, "What is 25 of 250?" opens the door to a wide range of mathematical concepts and real-world applications. Understanding fractions, percentages, and ratios is fundamental to various disciplines, from finance and science to everyday life. By mastering these concepts, you build a solid foundation for tackling more complex mathematical problems and making informed decisions in various situations. This exploration goes beyond a simple arithmetic calculation; it's about understanding the underlying principles and developing problem-solving skills that are transferable to numerous contexts. Remember to always approach mathematical problems systematically, breaking them down into manageable steps, and visualizing the relationships between the quantities involved. This will lead you to a clear and confident understanding of the solutions.
Latest Posts
Latest Posts
-
How Many Inches In 13cm
Sep 06, 2025
-
What Does Porpe Stand For
Sep 06, 2025
-
Early Detection Of Cancer
Sep 06, 2025
-
Nonliving Structural Part Of Bone
Sep 06, 2025
-
Is Kaitlin Olson A Twin
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 250 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.