What Is 25 Of 520
cibeltiagestion
Sep 10, 2025 · 5 min read
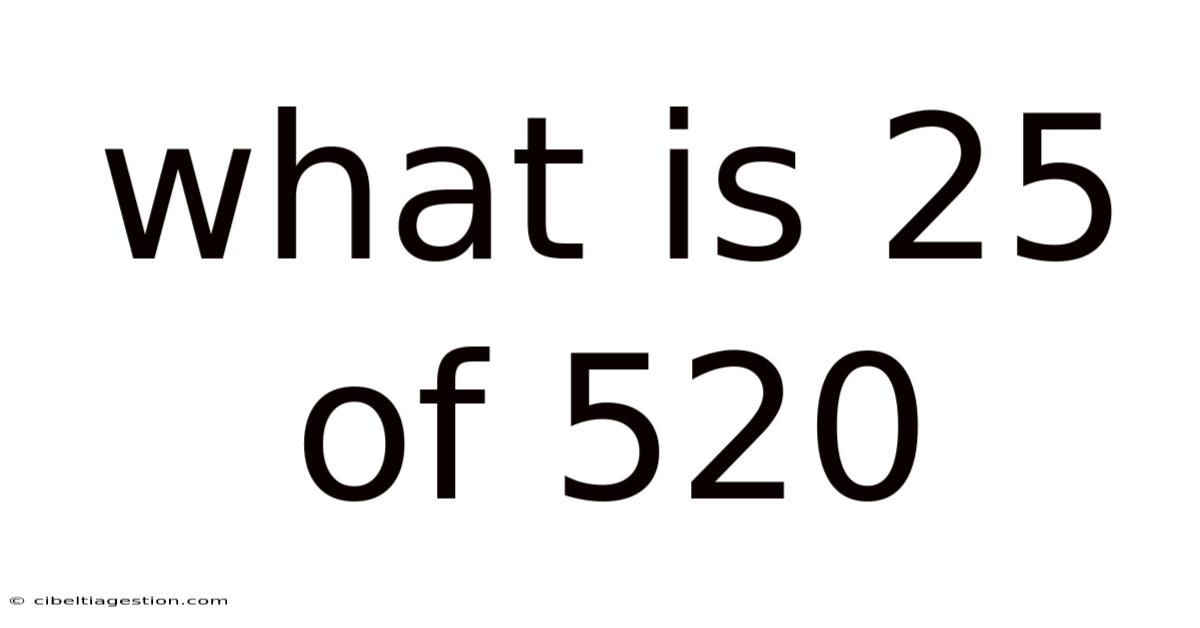
Table of Contents
What is 25/520? Understanding Fractions, Decimals, and Percentages
Finding out what 25/520 represents might seem like a simple arithmetic problem, but it offers a gateway to understanding fundamental mathematical concepts like fractions, decimals, and percentages – crucial tools in everyday life and various academic fields. This article will delve deep into this calculation, exploring various methods of simplification and providing context for broader applications.
Introduction: A Simple Fraction with Broad Implications
The fraction 25/520, at its core, represents a part of a whole. It means 25 out of 520 equal parts. While seemingly simple, understanding how to manipulate and interpret this fraction is a building block for more complex mathematical operations. This guide will not only calculate the value but also explain the processes involved, making it accessible to anyone, regardless of their prior mathematical experience. We'll cover simplification, converting to decimals and percentages, and explore real-world applications of these calculations.
Step-by-Step Simplification of 25/520
The first step in understanding 25/520 is to simplify the fraction. Simplification involves reducing the fraction to its lowest terms by finding the greatest common divisor (GCD) of the numerator (25) and the denominator (520).
-
Finding the GCD: The GCD is the largest number that divides both 25 and 520 without leaving a remainder. We can find this through prime factorization.
- Prime factorization of 25: 5 x 5 (or 5²)
- Prime factorization of 520: 2 x 2 x 2 x 5 x 13 (or 2³ x 5 x 13)
The common factor between 25 and 520 is 5.
-
Dividing the Numerator and Denominator: We divide both the numerator and the denominator by the GCD (5):
- 25 ÷ 5 = 5
- 520 ÷ 5 = 104
-
Simplified Fraction: Therefore, the simplified form of 25/520 is 5/104. This fraction is now in its simplest form because there are no common factors other than 1 between 5 and 104.
Converting the Fraction to a Decimal
To convert the simplified fraction 5/104 into a decimal, we simply divide the numerator (5) by the denominator (104):
5 ÷ 104 ≈ 0.048076923
This decimal representation shows the approximate value of the fraction. Note that the decimal continues infinitely; we've rounded it to several decimal places for practical purposes. The level of precision needed depends on the context of the problem. For many applications, rounding to two or three decimal places (0.048 or 0.0481) would be sufficient.
Converting the Fraction to a Percentage
A percentage expresses the fraction as a proportion of 100. To convert the decimal 0.048076923 (or the fraction 5/104) to a percentage, we multiply by 100:
0.048076923 x 100 ≈ 4.8076923%
Again, this is an approximation. For practical purposes, you might round this to 4.8% or 4.81%.
Understanding the Context and Applications
The significance of understanding the different representations of 25/520 – as a simplified fraction (5/104), a decimal (approximately 0.048), and a percentage (approximately 4.8%) – lies in its adaptability to various situations.
-
Proportion and Ratios: In many real-world scenarios, we deal with proportions and ratios. For example, if 25 out of 520 students in a school received a specific award, 5/104 represents the proportion of award recipients to the total number of students. This can be useful for comparing results across different years or schools.
-
Data Analysis: In data analysis, percentages are commonly used to represent data as proportions of the whole. The percentage approximately 4.8% could be used in graphs, charts, and reports to visualize the proportion of award-winning students.
-
Financial Calculations: Fractions and percentages are essential in financial calculations, such as calculating interest rates, discounts, or profit margins.
-
Probability and Statistics: In probability and statistics, fractions and decimals are used to represent probabilities and proportions within data sets. For example, if an event has a probability of 5/104, this means there's approximately a 4.8% chance of the event occurring.
Further Exploration: Working with Fractions
Let's explore some related concepts and techniques useful when working with fractions:
-
Adding and Subtracting Fractions: To add or subtract fractions, they must have a common denominator. For example, to add 5/104 and another fraction, you would need to find a common denominator before performing the addition.
-
Multiplying Fractions: Multiplying fractions is relatively straightforward: multiply the numerators together and the denominators together. For example, (5/104) x (2/3) = 10/312. This can then be simplified.
-
Dividing Fractions: To divide fractions, invert the second fraction (the divisor) and then multiply. For example, (5/104) ÷ (1/2) = (5/104) x (2/1) = 10/104. This can also be simplified.
Frequently Asked Questions (FAQ)
-
Q: Can 25/520 be simplified further than 5/104?
- A: No. 5 and 104 share no common factors other than 1, making 5/104 the simplest form of the fraction.
-
Q: What is the exact decimal value of 5/104?
- A: The exact decimal value is a non-terminating, repeating decimal. We use approximations (like 0.048) for practical purposes.
-
Q: Why is simplification important?
- A: Simplification makes fractions easier to understand, compare, and work with in calculations. It makes the numbers manageable and reduces the risk of errors.
-
Q: Are there other ways to find the GCD of 25 and 520?
- A: Yes, the Euclidean algorithm is another efficient method for finding the greatest common divisor.
Conclusion: Mastering the Fundamentals
Understanding the calculation and simplification of 25/520 is not just about arriving at the answer (approximately 0.048 or 4.8%). It's about grasping the foundational concepts of fractions, decimals, and percentages, and how these interconnected concepts are crucial tools across numerous fields. By mastering these fundamental skills, you'll be better equipped to handle more complex mathematical problems and solve real-world challenges that involve proportions, ratios, and quantitative analysis. Remember that practice is key; the more you work with fractions, decimals, and percentages, the more comfortable and confident you will become.
Latest Posts
Latest Posts
-
Did Rockefeller Use Horizontal Integration
Sep 10, 2025
-
1 10 Is Equivalent To
Sep 10, 2025
-
Noble Gas Configuration For Mercury
Sep 10, 2025
-
Defg Is An Isosceles Trapezoid
Sep 10, 2025
-
How Are New Viruses Made
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 520 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.