What Is 30 Of 100
cibeltiagestion
Sep 16, 2025 · 5 min read
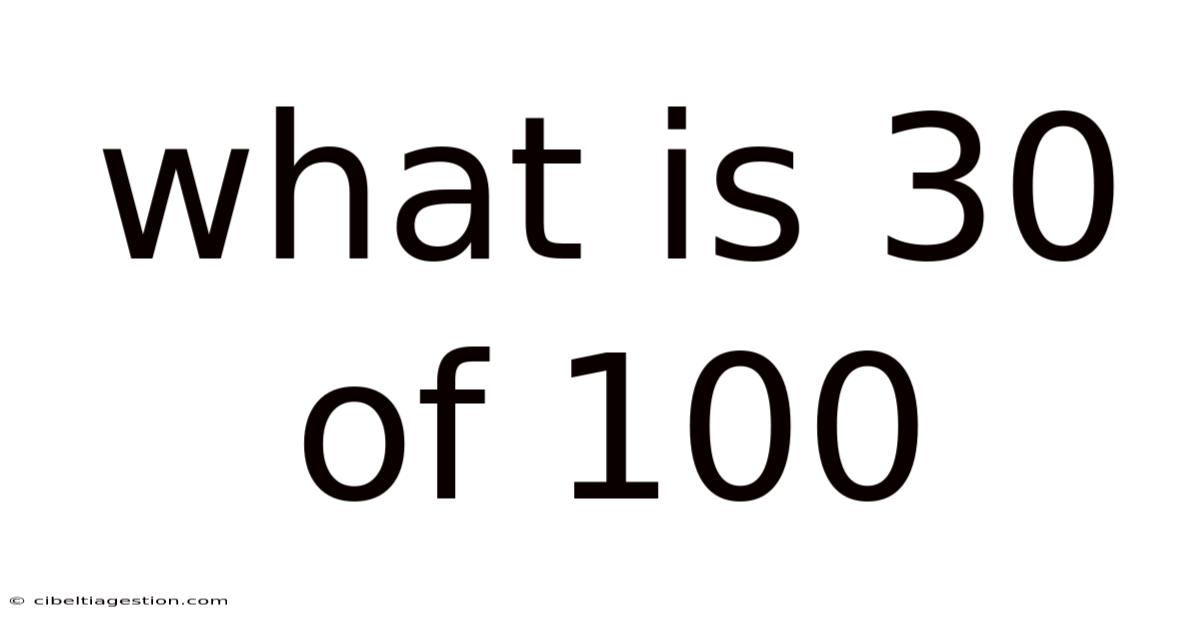
Table of Contents
What is 30% of 100? Understanding Percentages and Their Applications
Percentages are a fundamental concept in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to understanding statistics and financial data. This article will delve into the seemingly simple question: "What is 30% of 100?" We'll explore the calculation, its underlying principles, and diverse real-world examples to solidify your understanding of percentages. This comprehensive guide aims to provide a robust grasp of this crucial mathematical concept, making it easy to solve similar percentage problems independently.
Understanding Percentages
Before diving into the calculation, let's establish a firm understanding of what percentages represent. A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of 100" (from the Latin "per centum"). Therefore, 30% means 30 out of 100, or 30/100.
Calculating 30% of 100
There are several ways to calculate 30% of 100. Let's explore the most common methods:
Method 1: Using the Fraction Equivalent
As mentioned earlier, 30% is equivalent to the fraction 30/100. To find 30% of 100, we simply multiply the fraction by 100:
(30/100) * 100 = 30
Therefore, 30% of 100 is 30.
Method 2: Converting Percentage to Decimal
To convert a percentage to a decimal, we divide the percentage by 100. In this case, 30% becomes 0.30 (or simply 0.3). Then, we multiply this decimal by 100:
0.30 * 100 = 30
Again, we arrive at the answer: 30% of 100 is 30.
Method 3: Using Proportions
We can also solve this problem using proportions. We set up a proportion where x represents the unknown value (30% of 100):
x/100 = 30/100
To solve for x, we cross-multiply:
100x = 3000
Then, we divide both sides by 100:
x = 30
This confirms that 30% of 100 is 30.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial for navigating various aspects of daily life. Here are some examples:
-
Discounts: Imagine a store offering a 30% discount on a $100 item. Using our calculation, we know the discount amounts to $30, making the final price $70.
-
Taxes: If a 30% sales tax is applied to a $100 purchase, the tax amount would be $30, bringing the total cost to $130.
-
Grade Calculations: Suppose you scored 30 out of 100 on a test. This represents 30% of the total points.
-
Surveys and Statistics: Percentage calculations are essential for interpreting survey results and statistical data. For example, if 30% of 100 respondents prefer a particular product, this signifies a significant preference level.
-
Financial Calculations: Percentage calculations are used extensively in finance, such as calculating interest rates, investment returns, and loan payments. Understanding percentage changes in stock prices or investment portfolios is vital for successful investing.
-
Data Analysis: Percentages are frequently used to represent proportions and trends within datasets. Analyzing percentage changes over time provides valuable insights into growth or decline.
-
Cooking and Baking: Recipes often involve percentages when referring to ingredient proportions. For example, a recipe might specify 30% of the total weight should be flour.
Beyond the Basics: Understanding Percentage Change
While this article focuses on calculating a percentage of a number, it's crucial to also understand percentage change. Percentage change calculates the relative increase or decrease in a value over time or compared to another value. The formula is:
Percentage Change = [(New Value - Old Value) / Old Value] * 100
For example, if a value increases from 100 to 130, the percentage change is:
[(130 - 100) / 100] * 100 = 30%
This indicates a 30% increase. Conversely, if the value decreases from 100 to 70, the percentage change is:
[(70 - 100) / 100] * 100 = -30%
This indicates a 30% decrease. Understanding percentage change is essential for analyzing trends and making informed decisions in various fields.
Advanced Percentage Problems and Solutions
Let's explore some more complex problems to further enhance your understanding:
Problem 1: What is 15% of 250?
Solution: 0.15 * 250 = 37.5
Problem 2: If 20% of a number is 50, what is the number?
Solution: Let x represent the number. We can set up the equation: 0.20x = 50. Solving for x, we get x = 250.
Problem 3: A shirt is priced at $80 and is discounted by 25%. What is the final price?
Solution: The discount is 0.25 * $80 = $20. Therefore, the final price is $80 - $20 = $60.
Problem 4: A store increased the price of an item from $50 to $65. What is the percentage increase?
Solution: Using the percentage change formula: [(65 - 50) / 50] * 100 = 30%. The price increased by 30%.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate percentages?
A: The easiest method often depends on the specific problem. Using the decimal equivalent is generally efficient for most calculations.
Q: How can I calculate percentages without a calculator?
A: For simpler percentages like 10%, 25%, or 50%, you can use mental math. For others, breaking down the percentage into smaller, easier-to-calculate parts can be helpful. For example, 30% can be broken down into 10% + 10% + 10%.
Q: Why are percentages important?
A: Percentages provide a standardized way to compare proportions and make informed decisions across various fields, from finance to science to everyday life.
Q: Where can I find more practice problems?
A: Numerous online resources and textbooks offer practice problems on percentages. Searching for "percentage problems worksheets" or "percentage practice exercises" will yield many results.
Conclusion
The seemingly simple question, "What is 30% of 100?" serves as a gateway to understanding a much broader mathematical concept with far-reaching applications. This article has explored the calculation using multiple methods, highlighting its practical relevance across various domains. By grasping the principles of percentage calculation and practicing problem-solving, you can confidently tackle various percentage-related challenges in your academic pursuits, professional endeavors, and daily life. Remember that mastering percentages is not just about memorizing formulas, but about understanding the underlying concepts and applying them effectively to solve real-world problems. The more you practice, the more comfortable and proficient you will become with percentage calculations.
Latest Posts
Latest Posts
-
75 Of What Is 36
Sep 16, 2025
-
Cu No3 2 Compound Name
Sep 16, 2025
-
9e 4 5e 14 13e
Sep 16, 2025
-
Parting With Such Sweet Sorrow
Sep 16, 2025
-
The Practice Of Statistics 5e
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.