What Is 40 Of 160
cibeltiagestion
Sep 11, 2025 · 5 min read
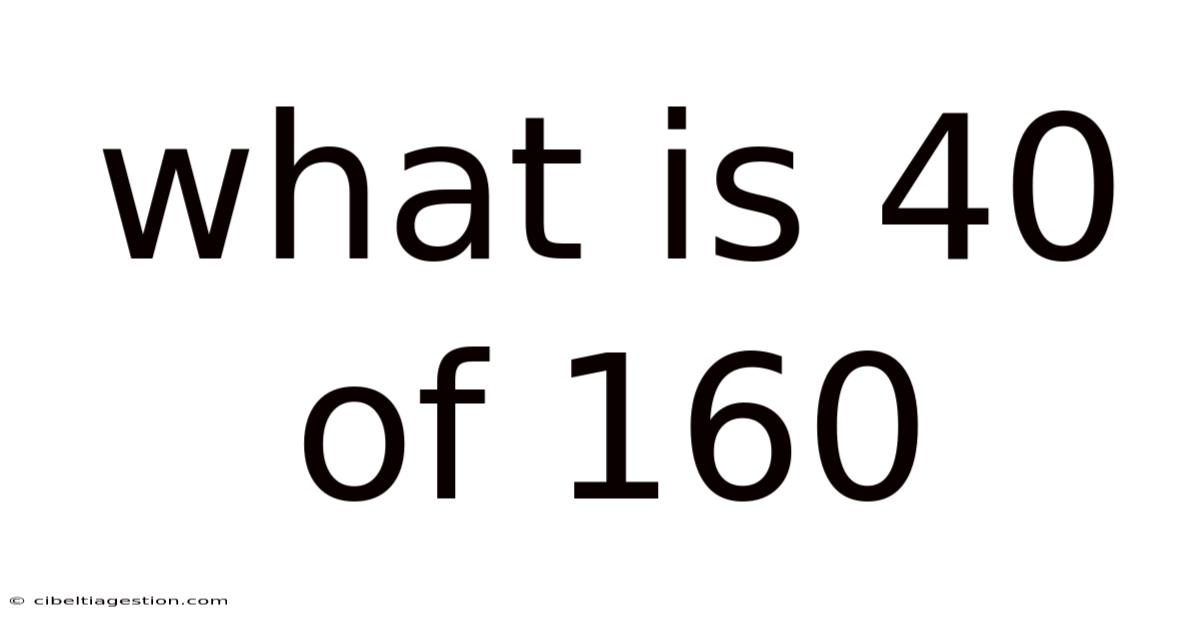
Table of Contents
What is 40 of 160? Understanding Percentages and Proportions
Finding "40 of 160" involves understanding percentages and proportions, fundamental concepts in mathematics with wide-ranging applications in everyday life, from calculating discounts to understanding statistical data. This article will not only answer the question directly but also delve into the underlying mathematical principles, providing you with the tools to solve similar problems independently. We'll explore different methods for calculating percentages, discuss the importance of proportional reasoning, and address frequently asked questions. By the end, you'll have a solid grasp of how to tackle percentage problems confidently.
Understanding the Question: "40 of 160"
The phrase "40 of 160" implicitly asks for the percentage or proportion that 40 represents when compared to 160. In simpler terms, it's asking: what fraction of 160 is 40? This is a classic percentage problem, and we can approach it using several methods.
Method 1: Using the Percentage Formula
The most straightforward way to solve this is to use the basic percentage formula:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 40
- Whole: 160
Substituting these values into the formula:
(40 / 160) * 100% = 25%
Therefore, 40 is 25% of 160.
Method 2: Simplifying the Fraction
Before applying the percentage formula, we can simplify the fraction 40/160. Both the numerator (40) and the denominator (160) are divisible by 40:
40 / 160 = 1 / 4
Now, converting the simplified fraction 1/4 to a percentage:
(1 / 4) * 100% = 25%
This method demonstrates that simplifying fractions can often make calculations easier and faster.
Method 3: Using Proportions
Proportions provide another powerful approach to solving percentage problems. A proportion is an equation stating that two ratios are equal. We can set up a proportion to represent the problem:
40 / 160 = x / 100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we can cross-multiply:
40 * 100 = 160 * x
4000 = 160x
x = 4000 / 160
x = 25
Therefore, 40 is 25% of 160. This method highlights the relationship between fractions and percentages.
The Importance of Proportional Reasoning
Understanding proportions is crucial in various contexts. It's essential for:
- Scaling recipes: Adjusting ingredient quantities based on the number of servings.
- Map reading: Interpreting distances and scales.
- Financial calculations: Determining interest rates, discounts, and profits.
- Scientific experiments: Analyzing data and drawing conclusions.
- Everyday problem-solving: Making comparisons and estimations.
Mastering proportional reasoning enhances your ability to solve a broad range of practical problems, making you a more efficient and effective problem-solver.
Expanding the Understanding: Beyond the Basics
While the core question is answered, let's expand our understanding by exploring related concepts:
-
Finding the Whole: If we knew that 40 represented 25% of a number, we could use the percentage formula to find the whole:
25% = 40 / Whole
0.25 * Whole = 40
Whole = 40 / 0.25
Whole = 160
-
Finding the Part: If we knew that a certain percentage of 160 was unknown, we could adapt the formula to find the part. For example, what is 15% of 160?
(15/100) * 160 = 24
-
Working with Different Percentages: The same methods apply regardless of the percentage. For example, finding 75% of 160 would involve substituting 75 for the percentage in the formula:
(75 / 100) * 160 = 120
Practical Applications: Real-world examples
Percentage calculations are integral to many real-life scenarios. Here are some examples:
- Sales and Discounts: If a store offers a 20% discount on an item priced at $160, the discount amount would be (20/100) * $160 = $32. The final price would be $160 - $32 = $128.
- Tax Calculations: Calculating sales tax or income tax involves percentage calculations based on the taxable amount.
- Grade Calculations: Determining your final grade in a course often requires calculating weighted averages, which utilize percentages.
- Financial Investments: Understanding interest rates and returns on investments requires knowledge of percentage calculations.
- Data Analysis: Percentages are used extensively to represent data in charts, graphs, and reports.
Frequently Asked Questions (FAQ)
Q1: What is the easiest way to calculate percentages?
A1: The easiest method often depends on the specific problem. The percentage formula ((Part / Whole) * 100%) is a versatile and reliable approach. Simplifying fractions before calculation can also streamline the process. Using a calculator can aid in speed and accuracy, particularly for more complex problems.
Q2: Can I use a calculator to solve these problems?
A2: Absolutely! Calculators are efficient tools for percentage calculations, especially when dealing with larger numbers or more complex problems. Simply input the numbers according to the percentage formula.
Q3: What if the numbers aren't whole numbers?
A3: The same methods apply whether the numbers are whole numbers or decimals. Use the percentage formula, simplify fractions where possible, and apply the same principles of proportional reasoning.
Q4: Are there any online calculators for percentages?
A4: Many online calculators are available specifically designed to perform percentage calculations. These can be helpful for quick calculations or for checking your work.
Conclusion: Mastering Percentages for a Brighter Future
Understanding percentages and proportions is a fundamental skill with vast applications in many aspects of life. By mastering these concepts, you'll be better equipped to tackle various challenges—from everyday financial decisions to more complex mathematical problems. Remember the core percentage formula, the power of simplifying fractions, and the versatility of proportional reasoning. Practice regularly, and you'll soon find that working with percentages becomes second nature. The ability to confidently calculate percentages not only improves your mathematical skills but also empowers you to make informed decisions and analyze information critically. Continue exploring related mathematical concepts, and your understanding of the world around you will continue to expand.
Latest Posts
Latest Posts
-
Most Back Disorders Caused By
Sep 11, 2025
-
What Is 97 8 In Celsius
Sep 11, 2025
-
58 Degrees Fahrenheit To Celsius
Sep 11, 2025
-
How Was Persian Coinage Sophisticated
Sep 11, 2025
-
Summarizing Can Be Used To
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 40 Of 160 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.