What Is 40 Of 35
cibeltiagestion
Sep 09, 2025 · 5 min read
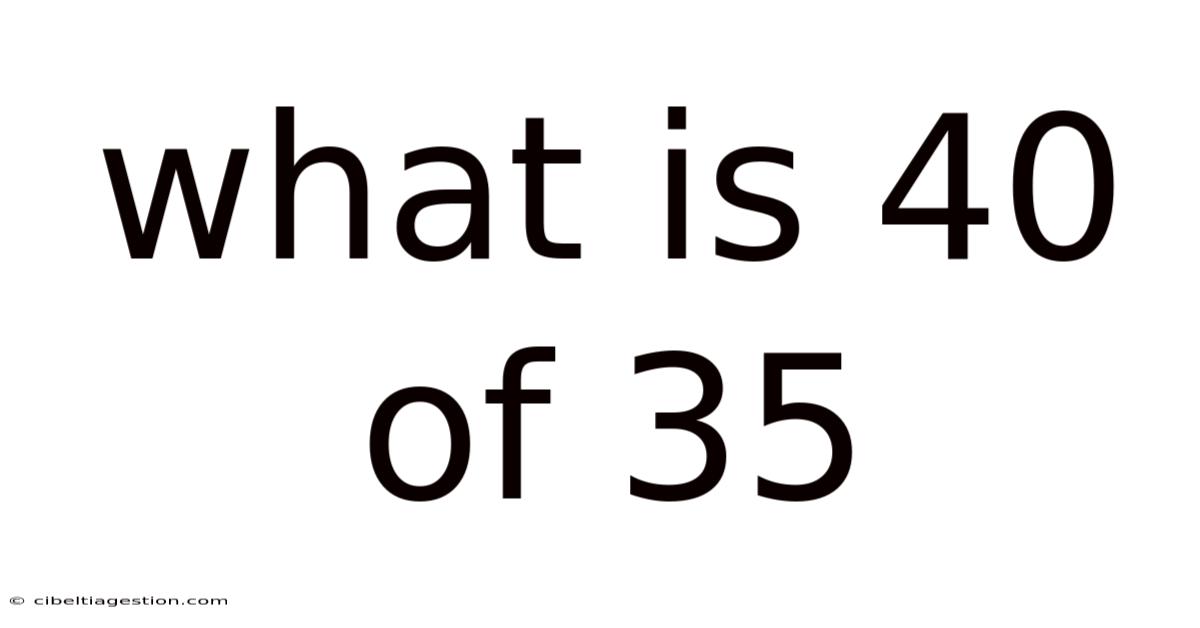
Table of Contents
What is 40% of 35? A Deep Dive into Percentages and Their Applications
Finding 40% of 35 might seem like a simple arithmetic problem, but it opens the door to understanding a fundamental concept in mathematics and its widespread applications in everyday life. This article will not only show you how to calculate 40% of 35 but also explore the underlying principles of percentages, different methods for calculating them, and real-world examples where this type of calculation is crucial. We'll delve into the practical implications and even touch upon some advanced concepts. By the end, you'll be confident in tackling percentage problems and appreciating their significance.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself derives from the Latin "per centum," meaning "out of a hundred." So, 40% means 40 out of 100, or 40/100, which can be simplified to 2/5. This fraction represents a ratio: a comparison of two quantities. In the context of "40% of 35," we're looking for 40/100 of the quantity 35.
Methods for Calculating 40% of 35
Several methods can be used to find 40% of 35. Let's explore the most common ones:
1. Using the Decimal Equivalent:
The simplest method involves converting the percentage to its decimal equivalent. To do this, divide the percentage by 100. In this case:
40% ÷ 100 = 0.40
Then, multiply this decimal by the number you're finding the percentage of:
0.40 x 35 = 14
Therefore, 40% of 35 is $\boxed{14}$.
2. Using Fractions:
As mentioned earlier, 40% can be expressed as the fraction 40/100 or its simplified form, 2/5. We can then use this fraction to calculate:
(2/5) x 35 = (2 x 35) / 5 = 70 / 5 = 14
Again, we arrive at the answer: $\boxed{14}$.
3. Using Proportions:
A proportion is an equation stating that two ratios are equal. We can set up a proportion to solve for 40% of 35:
40/100 = x/35
To solve for x (which represents 40% of 35), cross-multiply:
40 x 35 = 100x
1400 = 100x
x = 1400 / 100 = 14
This method reinforces the concept of ratios and proportions, demonstrating that the percentage represents a proportional relationship.
4. Using a Calculator:
Most calculators have a percentage function. Simply enter 40%, followed by the multiplication symbol, then 35. The calculator will directly provide the answer: $\boxed{14}$.
Real-World Applications of Percentage Calculations
Understanding how to calculate percentages is essential in numerous real-life situations:
-
Sales and Discounts: Calculating discounts on sale items. For example, a 40% discount on a $35 shirt would mean a saving of $14.
-
Taxes: Determining the amount of sales tax or income tax owed.
-
Tips and Gratuities: Calculating the appropriate tip amount in a restaurant.
-
Interest Rates: Calculating simple or compound interest on loans or investments. Understanding interest rates is crucial for making informed financial decisions.
-
Financial Statements: Analyzing financial statements, such as income statements and balance sheets, often requires working with percentages to understand key ratios and metrics. This includes profit margins, debt-to-equity ratios, and return on investment (ROI).
-
Statistics and Data Analysis: Percentages are fundamental in summarizing and interpreting data. For instance, expressing survey results or the success rate of a particular treatment.
-
Scientific Calculations: Percentages are used extensively in various scientific fields, including chemistry (concentration of solutions), biology (population growth), and physics (efficiency of machines).
Beyond the Basics: Advanced Percentage Concepts
While calculating 40% of 35 is straightforward, let's explore some more complex percentage problems:
-
Finding the Percentage: If you know the part and the whole, you can calculate the percentage. For example, if 14 out of 35 students passed an exam, what percentage passed? This is solved by dividing the part (14) by the whole (35) and multiplying by 100: (14/35) x 100 = 40%.
-
Finding the Whole: If you know the percentage and the part, you can find the whole. For example, if 40% of a number is 14, what is the number? This requires setting up an equation: 0.4x = 14. Solving for x, we get x = 14/0.4 = 35.
-
Compound Interest: Compound interest involves earning interest on both the principal amount and accumulated interest. This is a more complex calculation that requires understanding exponential growth.
-
Percentage Increase and Decrease: Calculating the percentage change between two values. For example, if the price of an item increased from $35 to $49, the percentage increase would be calculated as: [(49-35)/35] x 100 = 40%.
Frequently Asked Questions (FAQs)
Q: What are some common mistakes people make when calculating percentages?
A: Common mistakes include incorrectly converting percentages to decimals, mixing up the numerator and denominator when using fractions, and not understanding the context of the problem. Always double-check your work and ensure you are applying the correct method.
Q: How can I improve my understanding of percentages?
A: Practice is key! Work through various percentage problems, starting with simple ones and gradually increasing the complexity. Use online resources, textbooks, and practice worksheets to solidify your understanding.
Q: Are there any online tools or calculators that can help with percentage calculations?
A: Yes, many online calculators and websites are specifically designed for percentage calculations. These tools can be helpful for checking your work or for solving more complex problems.
Q: What if I need to calculate a percentage of a percentage?
A: Calculating a percentage of a percentage involves multiplying the percentages as decimals. For example, finding 20% of 40% would be 0.20 x 0.40 = 0.08, or 8%.
Conclusion
Calculating 40% of 35, which equals 14, is a seemingly simple task, but it underscores a powerful mathematical concept with far-reaching applications. Mastering percentage calculations is essential for navigating various aspects of daily life, from personal finance to professional endeavors. By understanding the different methods and applying them to real-world scenarios, you'll not only be able to solve percentage problems efficiently but also gain a deeper appreciation for their importance in the world around us. Continue practicing and exploring different percentage problems to build confidence and strengthen your mathematical skills. Remember, consistent practice is the key to mastering this fundamental mathematical concept.
Latest Posts
Latest Posts
-
Ice Melts In Iceboxes Because
Sep 09, 2025
-
Titration Pre Lab Questions Answers
Sep 09, 2025
-
What Is 8 Times 4
Sep 09, 2025
-
Convert 46 Celsius To Fahrenheit
Sep 09, 2025
-
Cross Sectional Area Of The Cylinder
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 40 Of 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.