What Is 70 Of 50
cibeltiagestion
Sep 15, 2025 · 5 min read
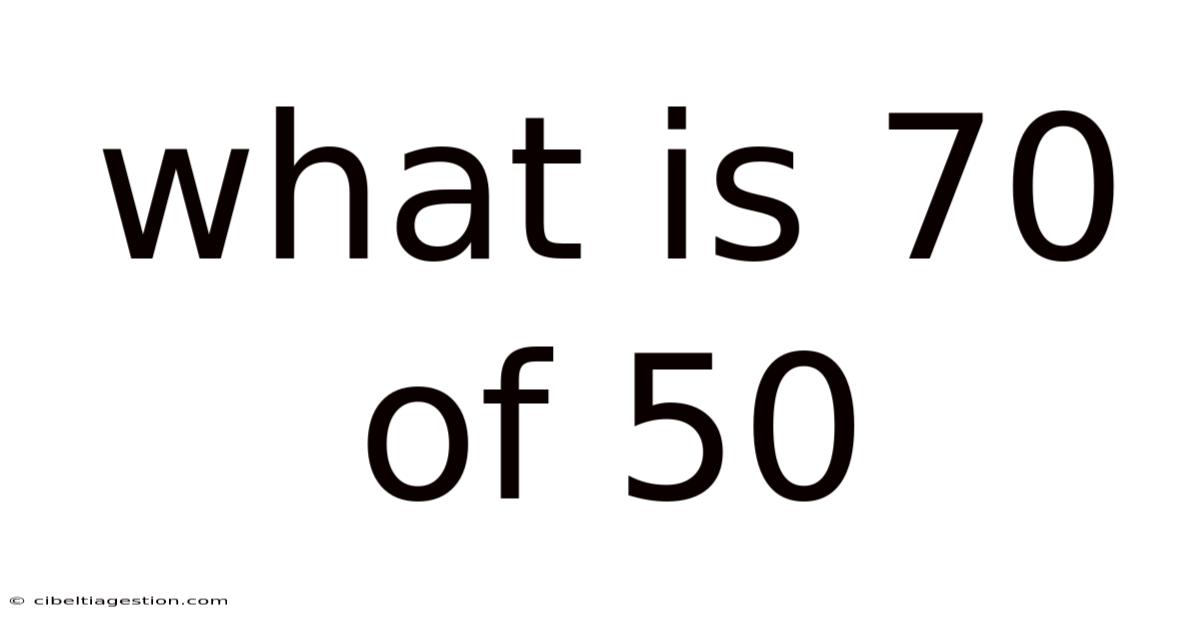
Table of Contents
What is 70% of 50? A Deep Dive into Percentages and Their Applications
Finding 70% of 50 might seem like a simple arithmetic problem, but understanding the underlying concepts of percentages opens doors to a vast world of applications in various fields. This article will not only answer the question "What is 70% of 50?" but also explore the meaning of percentages, different methods to calculate them, and their practical relevance in everyday life, from finance to science. This comprehensive guide will equip you with the knowledge to confidently tackle percentage problems of any complexity.
Understanding Percentages: The Foundation
A percentage is a fraction or a ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" and is represented by the symbol %. For example, 70% means 70 out of 100, or 70/100, which simplifies to 7/10. This fundamental understanding forms the bedrock for all percentage calculations.
Calculating 70% of 50: Three Methods
There are several ways to calculate 70% of 50. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. We convert the percentage to its decimal equivalent by dividing by 100. 70% becomes 70/100 = 0.7. Then, we multiply this decimal by the number we're finding the percentage of:
0.7 * 50 = 35
Therefore, 70% of 50 is 35.
Method 2: Using Fractions
As mentioned earlier, 70% can be expressed as the fraction 70/100. We can simplify this fraction to 7/10. Now, we multiply this simplified fraction by 50:
(7/10) * 50 = 7 * (50/10) = 7 * 5 = 35
Again, we arrive at the answer: 35. This method highlights the relationship between percentages, fractions, and decimals.
Method 3: Proportions
This method is particularly useful for understanding the underlying relationship between the percentage and the whole. We set up a proportion:
70/100 = x/50
Where 'x' represents the unknown value (70% of 50). To solve for x, we cross-multiply:
70 * 50 = 100 * x
3500 = 100x
x = 3500/100 = 35
This method emphasizes the concept of ratios and reinforces the proportional relationship between percentages and the quantities they represent.
Beyond the Calculation: Real-World Applications
The seemingly simple calculation of 70% of 50 has broad implications across numerous disciplines:
1. Finance and Business:
- Discounts and Sales: Stores frequently offer discounts expressed as percentages. Calculating the actual discount amount is crucial for consumers to determine the final price. For example, a 70% discount on a $50 item would be $35, resulting in a final price of $15.
- Profit Margins: Businesses use percentages to calculate profit margins—the difference between the cost of goods and the selling price.
- Interest Rates: Understanding interest rates, often expressed as percentages, is vital for managing personal finances, loans, and investments. Calculating the interest on a loan or the return on an investment involves percentage calculations.
- Tax Calculations: Sales tax, income tax, and other taxes are usually expressed as percentages. Accurate calculation of tax amounts relies heavily on percentage computations.
2. Science and Statistics:
- Data Analysis: Percentages are fundamental in statistical analysis, allowing researchers to express proportions and trends within datasets. For example, a researcher might find that 70% of participants in a study exhibited a specific behavior.
- Scientific Experiments: In scientific experiments, data is often expressed as percentages to represent the success rate of a treatment or the occurrence of a particular event.
- Probability: Percentages are often used to represent probabilities in various fields, such as weather forecasting or risk assessment.
3. Everyday Life:
- Tipping: Calculating a tip in a restaurant usually involves determining a percentage of the total bill.
- Grading Systems: Many educational institutions use percentages to express student grades and overall performance.
- Recipe Adjustments: When scaling recipes up or down, understanding percentages helps maintain the correct proportions of ingredients.
Expanding Your Understanding: More Complex Percentage Problems
While finding 70% of 50 is a relatively simple calculation, the principles extend to more complex scenarios:
- Finding the Percentage: You might be given the part and the whole and need to find the percentage. For example, if 35 out of 50 students passed an exam, what percentage passed? This involves dividing the part (35) by the whole (50) and multiplying by 100.
- Finding the Whole: You might know the percentage and the part and need to find the whole. For example, if 35 represents 70% of a certain amount, what is that amount? This requires setting up a proportion or using algebraic methods to solve for the unknown.
Mastering percentage calculations involves understanding the fundamental principles and practicing different types of problems.
Frequently Asked Questions (FAQ)
Q: What are some common mistakes people make when calculating percentages?
A: Common mistakes include:
- Confusing the percentage with the decimal equivalent: Incorrectly using the percentage directly in calculations instead of its decimal form (e.g., using 70 instead of 0.7).
- Incorrectly setting up proportions: Errors in cross-multiplication or solving for the unknown variable in proportional equations.
- Misinterpreting the problem: Failing to clearly identify the part and the whole in a problem statement.
Q: Are there any shortcuts for calculating percentages mentally?
A: Yes, several shortcuts exist, especially for common percentages like 10%, 25%, and 50%.
- 10%: Simply move the decimal point one place to the left. 10% of 50 is 5.
- 25%: Divide by 4. 25% of 50 is 12.5
- 50%: Divide by 2. 50% of 50 is 25.
Q: How can I improve my skills in calculating percentages?
A: The best way to improve is through consistent practice. Start with simple problems, gradually increasing the difficulty level. Use online resources, textbooks, or practice worksheets to reinforce your understanding and build confidence.
Conclusion
Calculating 70% of 50, while seemingly straightforward, provides a gateway to understanding the broader applications of percentages. From navigating everyday financial transactions to comprehending complex scientific data, the ability to work with percentages is a crucial skill in various aspects of life. By grasping the fundamental principles and practicing different calculation methods, you can confidently tackle percentage problems of any complexity and unlock the power of this fundamental mathematical concept. Remember that the key lies not just in the answer (35), but in the understanding of the process and its widespread applicability.
Latest Posts
Latest Posts
-
The Law Demand States That
Sep 15, 2025
-
Meaning Of Soft Shoulder Sign
Sep 15, 2025
-
Speed Limit For Blind Intersection
Sep 15, 2025
-
How Many Oz In 2l
Sep 15, 2025
-
5 8 Cup To 1 4 Cup
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 70 Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.