What Is 75 Of 200
cibeltiagestion
Sep 12, 2025 · 6 min read
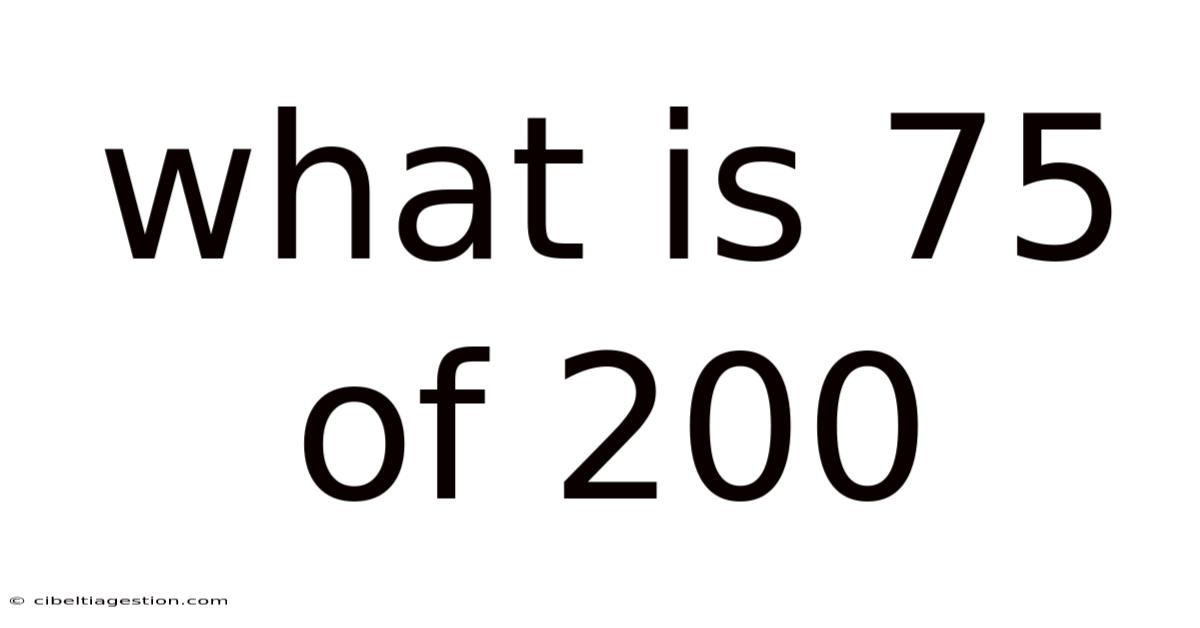
Table of Contents
What is 75% of 200? A Comprehensive Guide to Percentages
Finding 75% of 200 might seem like a simple arithmetic problem, but understanding the underlying concepts of percentages is crucial for various applications in everyday life, from calculating discounts to understanding financial reports. This comprehensive guide will not only answer the question "What is 75% of 200?" but also delve deeper into the mechanics of percentage calculations, offering practical examples and exploring related mathematical concepts.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The symbol % represents "per cent," meaning "out of one hundred." For instance, 75% means 75 out of 100, which can be written as the fraction 75/100 or the decimal 0.75. Understanding this fundamental concept is key to solving percentage problems.
Calculating 75% of 200: Three Methods
There are several ways to calculate 75% of 200. Let's explore three common methods:
Method 1: Using the Fraction Method
This method leverages the fraction equivalent of 75%. As mentioned earlier, 75% is equal to 75/100. To find 75% of 200, we simply multiply 200 by the fraction 75/100:
(75/100) * 200 = 150
Therefore, 75% of 200 is 150. This method is straightforward and easily understood, making it ideal for beginners.
Method 2: Using the Decimal Method
This method utilizes the decimal equivalent of 75%, which is 0.75. We multiply 200 by 0.75:
0.75 * 200 = 150
Again, the answer is 150. This method is efficient and commonly used in calculators and computer programs.
Method 3: Using Proportions
This method uses the concept of proportions to solve the problem. We set up a proportion:
75/100 = x/200
where 'x' represents the unknown value (75% of 200). To solve for x, we cross-multiply:
75 * 200 = 100 * x 15000 = 100x x = 15000 / 100 x = 150
This method demonstrates a more formal approach to solving percentage problems and is particularly useful for more complex scenarios.
Practical Applications of Percentage Calculations
Understanding percentages is vital in many real-world situations. Here are a few examples:
-
Discounts: Calculating discounts on sale items is a common application. If a $200 item is discounted by 75%, you would calculate 75% of $200 ($150) and subtract it from the original price ($200 - $150 = $50) to find the final price.
-
Taxes: Calculating sales tax or income tax involves determining a percentage of a given amount. For example, if the sales tax is 5% on a $200 purchase, you calculate 5% of $200 to find the tax amount.
-
Tips: Calculating a tip in a restaurant often involves finding a percentage of the total bill. A 20% tip on a $200 meal would be calculated as 20% of $200.
-
Financial Analysis: Percentages are extensively used in financial statements and reports to analyze financial performance, such as profit margins, return on investment (ROI), and debt-to-equity ratios.
-
Statistics: Percentages are frequently employed in statistical analysis to represent data and probabilities. For instance, expressing survey results or expressing the probability of an event occurring.
-
Science and Engineering: Percentages are used in various scientific and engineering calculations, particularly in expressing concentrations, efficiencies, and error margins.
Beyond the Basics: Exploring Related Concepts
While calculating 75% of 200 is a relatively simple calculation, understanding related concepts deepens your mathematical literacy. Let's explore some:
-
Finding the Percentage: If you know the part and the whole, you can find the percentage. For example, if 150 is a part of 200, what percentage is it? The calculation is: (150/200) * 100% = 75%. This is the reverse of our initial problem.
-
Finding the Whole: If you know a percentage and the part, you can find the whole. For example, if 150 represents 75% of a whole number, what is the whole number? The calculation is: (150 / 0.75) = 200.
-
Compound Percentages: These involve calculating percentages of percentages, often occurring in scenarios like interest calculations where interest is calculated on the principal plus accumulated interest.
-
Percentage Change: This measures the change in a value over time, expressed as a percentage. For instance, if a value increases from 100 to 150, the percentage increase is ((150-100)/100) * 100% = 50%.
Solving More Complex Percentage Problems
Let's look at some slightly more complex scenarios involving percentages:
Example 1: A store offers a 25% discount on a $200 item. Then, an additional 10% discount is applied to the discounted price. What is the final price?
First, calculate the 25% discount: 0.25 * $200 = $50. The discounted price is $200 - $50 = $150. Next, calculate the 10% discount on the discounted price: 0.10 * $150 = $15. The final price is $150 - $15 = $135.
Example 2: A stock increased by 15% from its initial value of $100. Then, it decreased by 10%. What is the final value of the stock?
First, calculate the 15% increase: 0.15 * $100 = $15. The increased value is $100 + $15 = $115. Next, calculate the 10% decrease: 0.10 * $115 = $11.50. The final value is $115 - $11.50 = $103.50. Note that this final value isn't simply the initial value plus the net percentage change (15% - 10% = 5%). The percentage change is calculated on the new value after each step.
These examples highlight the importance of understanding the order of operations and the impact of applying percentages sequentially.
Frequently Asked Questions (FAQ)
Q1: What is the easiest way to calculate percentages?
The easiest way depends on personal preference and the tools available. The decimal method is often the most efficient for quick calculations using a calculator. The fraction method is excellent for mental calculations or when dealing with simple fractions.
Q2: How can I calculate percentages without a calculator?
For simple percentages like 10%, 25%, or 50%, mental calculation is feasible. For others, converting the percentage to a fraction can simplify the calculation. For example, 30% is 3/10, making it easy to find 30% of a number by dividing by 10 and then multiplying by 3.
Q3: Are there any online tools to help with percentage calculations?
Yes, numerous websites and apps offer percentage calculators. These tools can handle various percentage-related calculations, from finding percentages to calculating percentage changes.
Q4: What if I need to calculate a percentage of a percentage?
You would multiply the percentages together. For instance, 10% of 20% is calculated as 0.10 * 0.20 = 0.02, or 2%.
Conclusion
This article provided a thorough explanation of how to calculate 75% of 200, using various methods. More importantly, it expanded on the broader concept of percentages, highlighting their diverse applications in everyday life, finance, science, and more. Mastering percentage calculations is a valuable skill that extends far beyond simple arithmetic problems, forming a crucial building block for more advanced mathematical concepts and practical problem-solving. Understanding the underlying principles and practicing different methods will equip you to confidently tackle a wide range of percentage-related challenges. Remember to always double-check your work and consider using different methods to verify your results. With practice, calculating percentages will become second nature, empowering you to navigate numerical challenges with greater ease and confidence.
Latest Posts
Latest Posts
-
Quotes From The Great Gatsby
Sep 12, 2025
-
Is A Hexagon A Parallelogram
Sep 12, 2025
-
The Neck Is A
Sep 12, 2025
-
How Old To Buy Lighter
Sep 12, 2025
-
Prove Abcd Is A Parallelogram
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 75 Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.