What Is 75 Of 300
cibeltiagestion
Sep 17, 2025 · 5 min read
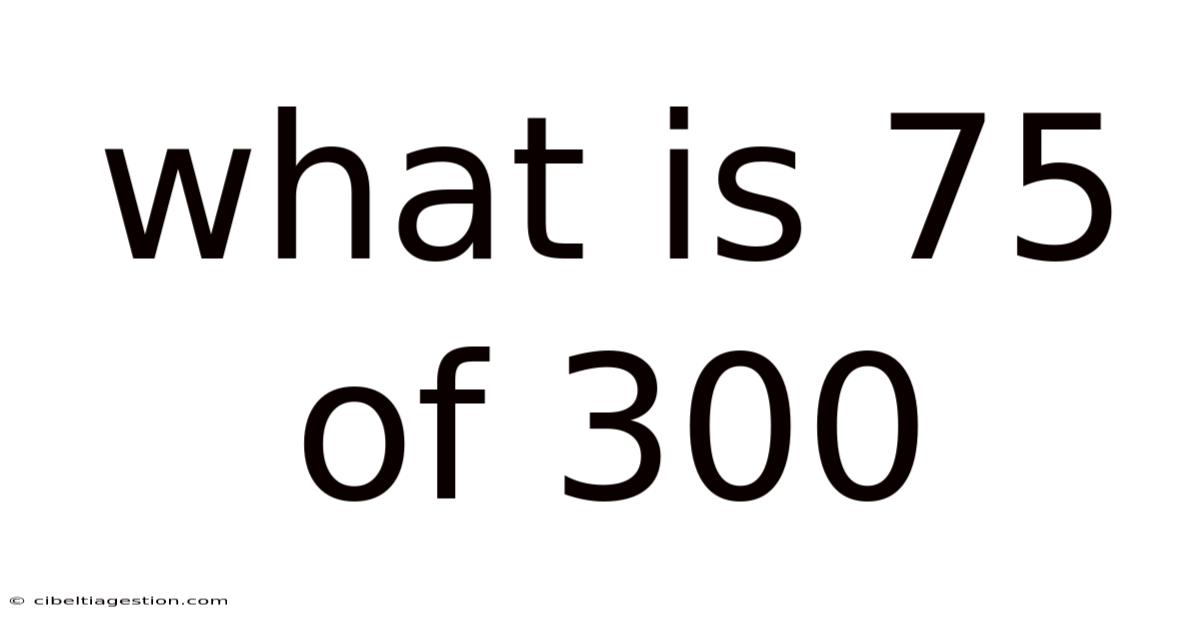
Table of Contents
What is 75% of 300? A Comprehensive Guide to Percentages and Their Applications
Finding 75% of 300 might seem like a simple calculation, but understanding the underlying principles of percentages opens doors to a wide range of applications in everyday life, from calculating discounts and sales tax to understanding financial reports and statistical data. This article will not only answer the question "What is 75% of 300?" but also delve into the methods used to solve percentage problems, explore different approaches, and highlight the importance of percentage calculations in various fields.
Understanding Percentages: A Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." Therefore, 75% can be interpreted as 75 parts out of 100 equal parts. This can be represented as a fraction (75/100) or a decimal (0.75). Understanding this fundamental concept is key to solving any percentage problem.
Method 1: The Fraction Method
This is arguably the most intuitive method, particularly for beginners. We convert the percentage into a fraction and then multiply it by the whole number.
-
Step 1: Convert the percentage to a fraction: 75% can be written as 75/100. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor (25), resulting in 3/4.
-
Step 2: Multiply the fraction by the whole number: Now, multiply the simplified fraction (3/4) by 300: (3/4) * 300 = 900/4 = 225
Therefore, 75% of 300 is 225.
Method 2: The Decimal Method
This method uses the decimal equivalent of the percentage.
-
Step 1: Convert the percentage to a decimal: 75% is equivalent to 0.75 (simply divide 75 by 100).
-
Step 2: Multiply the decimal by the whole number: Multiply 0.75 by 300: 0.75 * 300 = 225
Again, we arrive at the answer: 75% of 300 is 225.
Method 3: Using Proportions
This method is particularly useful for understanding the relationship between the percentage, the part, and the whole. We can set up a proportion:
- Set up the proportion: We know that 75% is to 100% as 'x' (the unknown value) is to 300. This can be written as:
75/100 = x/300
- Solve for x: To solve for x, we cross-multiply:
100x = 75 * 300
100x = 22500
x = 22500 / 100
x = 225
Therefore, 75% of 300 is 225.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-world scenarios:
-
Retail and Sales: Calculating discounts, sales tax, and final prices after discounts are applied. For example, a 25% discount on a $300 item can be easily calculated using these methods.
-
Finance: Understanding interest rates, calculating loan repayments, analyzing investment returns, and interpreting financial statements all rely heavily on percentage calculations. Compound interest, for instance, involves repeated percentage calculations.
-
Statistics and Data Analysis: Percentages are used extensively in presenting and interpreting data. For example, expressing survey results, analyzing market share, and calculating growth rates often involve percentages.
-
Science and Engineering: Percentage calculations are vital in various scientific and engineering applications, such as calculating efficiency, error margins, and concentration levels.
Beyond the Basics: More Complex Percentage Problems
While finding 75% of 300 is a relatively straightforward calculation, the principles can be applied to more complex scenarios:
-
Finding the percentage one number represents of another: For example, what percentage is 150 of 300? This involves dividing 150 by 300 and then multiplying by 100%.
-
Finding the original amount before a percentage increase or decrease: For example, if an item is currently priced at $225 after a 25% increase, what was the original price? This requires working backwards using the percentage change.
-
Calculating percentage change: Determining the percentage increase or decrease between two numbers is a common task in many fields. This involves finding the difference between the two numbers, dividing by the original number, and multiplying by 100%.
Troubleshooting and Common Mistakes
Several common errors can occur when dealing with percentage calculations:
-
Incorrect decimal conversion: Mistakes in converting percentages to decimals are frequent. Double-check your decimal conversion before proceeding with the calculation.
-
Order of operations: Ensure that you follow the correct order of operations (PEMDAS/BODMAS) when performing calculations involving percentages and other mathematical operations.
-
Incorrect interpretation of the problem: Carefully read and understand the problem statement before attempting to solve it. Identify the whole, the part, and the percentage correctly.
Frequently Asked Questions (FAQ)
Q1: How can I calculate percentages quickly without a calculator?
A1: For simple percentages like 10%, 25%, 50%, and 75%, you can use mental math techniques. For example, 10% is simply one-tenth of the number, 25% is one-quarter, and 50% is one-half. For others, consider breaking down the percentage into easier-to-calculate parts.
Q2: What if the percentage is not a whole number (e.g., 75.5%)?
A2: The same methods apply, simply convert the percentage to a decimal (0.755 in this case) and proceed with the multiplication.
Q3: Are there any online tools or calculators to help with percentage calculations?
A3: Yes, many free online calculators are available that can help you perform percentage calculations quickly and accurately. However, understanding the underlying principles is more valuable in the long run.
Q4: How can I improve my understanding of percentages?
A4: Practice is key! Work through various percentage problems, starting with simple ones and gradually increasing the complexity. Try to solve problems using different methods to reinforce your understanding.
Conclusion
Finding 75% of 300, as we've demonstrated, results in 225. However, the true value of this exercise lies not just in the answer itself but in grasping the fundamental concepts of percentages and their widespread applications. By understanding the different methods for calculating percentages, you equip yourself with a powerful tool applicable across various disciplines. The ability to confidently perform percentage calculations is a valuable skill that will serve you well throughout your life, both personally and professionally. From managing your finances to interpreting data, the ability to work with percentages is a cornerstone of numerical literacy.
Latest Posts
Latest Posts
-
4 Oz How Many Tablespoons
Sep 17, 2025
-
Beatriz Se Compromete Con Roberto
Sep 17, 2025
-
Where Does Shearing Often Occur
Sep 17, 2025
-
Reading Plus Level I Answers
Sep 17, 2025
-
What Is Homework Spelled Backwords
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 75 Of 300 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.