What Is 80 Of 24
cibeltiagestion
Sep 15, 2025 · 5 min read
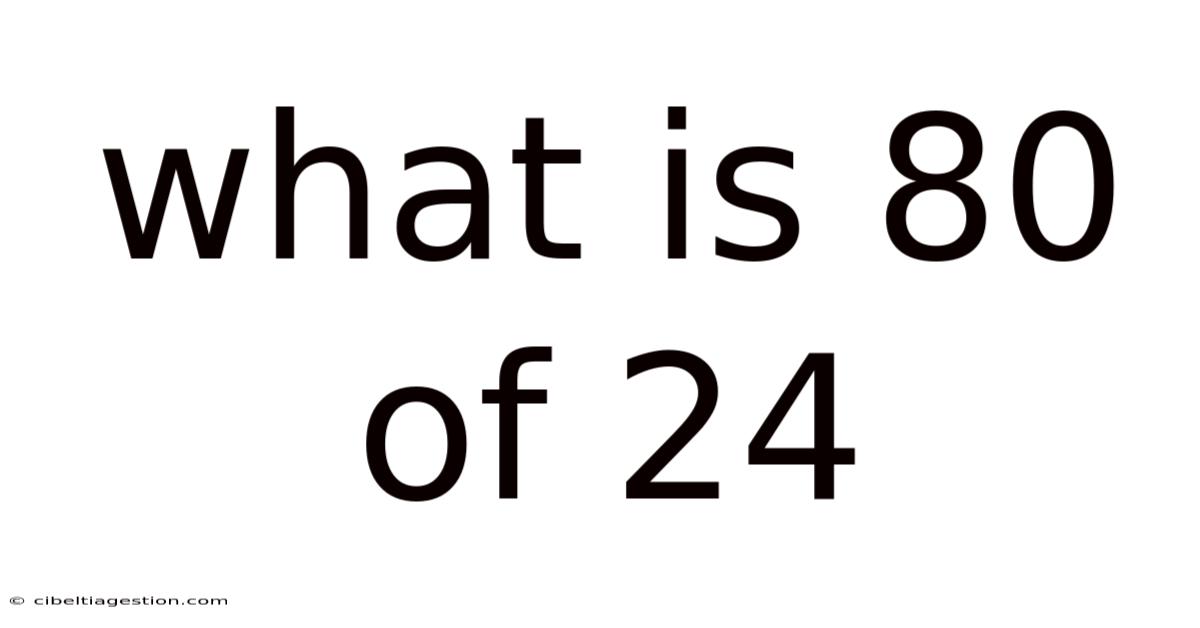
Table of Contents
What is 80% of 24? A Comprehensive Guide to Percentages and Calculations
Finding 80% of 24 might seem like a simple problem, but it opens the door to understanding a fundamental mathematical concept: percentages. This seemingly basic calculation is the cornerstone of many real-world applications, from calculating discounts and sales tax to understanding financial reports and statistical data. This article will not only solve the problem of "What is 80% of 24?" but will also delve into the underlying principles, providing you with a thorough understanding of percentages and various methods for solving percentage-related problems.
Understanding Percentages
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Understanding this fundamental concept is key to solving any percentage problem.
Method 1: Converting Percentage to Decimal
The most straightforward way to calculate 80% of 24 is to convert the percentage to a decimal and then multiply.
Steps:
-
Convert the percentage to a decimal: To do this, divide the percentage by 100. In this case, 80% becomes 80/100 = 0.8.
-
Multiply the decimal by the number: Multiply the decimal (0.8) by the number you want to find the percentage of (24). This gives us 0.8 * 24 = 19.2.
Therefore, 80% of 24 is 19.2.
Method 2: Using Fractions
Percentages can also be expressed as fractions. 80% can be written as 80/100. This fraction can be simplified to 4/5.
Steps:
-
Express the percentage as a fraction: 80% = 80/100 = 4/5
-
Multiply the fraction by the number: Multiply the simplified fraction (4/5) by the number (24): (4/5) * 24 = (4 * 24) / 5 = 96 / 5 = 19.2
Again, we arrive at the answer: 80% of 24 is 19.2.
Method 3: Proportion Method
This method uses the concept of proportion to solve percentage problems. We can set up a proportion to find the unknown value (x), which represents 80% of 24.
Steps:
-
Set up a proportion: We can write the proportion as: 80/100 = x/24
-
Cross-multiply: Cross-multiply to solve for x: 80 * 24 = 100 * x
-
Solve for x: 1920 = 100x => x = 1920 / 100 = 19.2
Therefore, 80% of 24 is 19.2.
Real-world Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-life situations:
-
Sales and Discounts: Calculating discounts offered on products during sales. For example, a 20% discount on a $100 item.
-
Taxes: Calculating sales tax or income tax on earnings or purchases.
-
Finance: Determining interest rates on loans, investments, and savings accounts. Understanding percentage changes in stock prices or investment portfolios.
-
Statistics: Analyzing statistical data, such as percentages of populations or survey results. For example, understanding the percentage of people who prefer a particular brand.
-
Tip Calculation: Calculating a tip at a restaurant based on the percentage of the bill.
-
Grade Calculation: Determining a student's grade based on the percentage of correct answers on an exam.
-
Commission: Calculating commission earned by salespeople based on a percentage of sales.
-
Profit Margin: Understanding the profit margin of a business, expressed as a percentage of revenue.
Advanced Percentage Calculations
While finding 80% of 24 is a relatively simple calculation, the principles can be applied to more complex problems. Consider these examples:
-
Finding the percentage increase or decrease: This involves calculating the percentage change between two numbers. For example, if a price increases from $50 to $60, the percentage increase is calculated as [(60-50)/50] * 100% = 20%.
-
Calculating the original value given a percentage: If you know the final value after a percentage increase or decrease, you can work backward to find the original value.
-
Calculating the percentage of a larger number: The methods discussed earlier apply equally well to larger numbers.
Frequently Asked Questions (FAQ)
Q: What if I need to find a percentage that's not a whole number, like 37.5% of 24?
A: You can use the same methods. Convert 37.5% to a decimal (0.375) and multiply by 24, or convert it to a fraction (37.5/100 = 3/8) and multiply by 24.
Q: Are there any shortcuts for calculating percentages mentally?
A: Yes, for certain percentages, there are mental shortcuts. For instance, 10% is simply moving the decimal point one place to the left. 5% is half of 10%. 25% is one-quarter, 50% is one-half, and so on. Practicing these can improve your mental calculation speed.
Q: What are some common mistakes people make when calculating percentages?
A: Common mistakes include incorrect decimal conversions, errors in multiplication or division, and not understanding the context of the problem. Carefully review your work and check your calculations to avoid these errors.
Q: What tools can assist in percentage calculations?
A: Calculators are the most common tool for percentage calculations. Many online calculators and spreadsheet programs (like Microsoft Excel or Google Sheets) also have built-in functions for calculating percentages.
Conclusion
Calculating 80% of 24, while seemingly simple, underscores the broader importance of understanding percentages. This fundamental mathematical concept is applicable across numerous fields, making it a crucial skill to master. By understanding the various methods outlined in this article, from converting percentages to decimals to utilizing proportions, you are equipped to tackle a wide range of percentage problems, both simple and complex. Remember to practice consistently to build proficiency and confidently apply your knowledge to real-world scenarios. The key is understanding the underlying principles, not just memorizing formulas. With consistent practice and a clear understanding of the concepts, you can become proficient in percentage calculations and confidently apply this skill in various aspects of your life.
Latest Posts
Latest Posts
-
73 Inches Is How Tall
Sep 15, 2025
-
4 Gallons How Many Pints
Sep 15, 2025
-
How Do You Spell Mississippi
Sep 15, 2025
-
How Many Electrons In Hydrogen
Sep 15, 2025
-
Which Region Most Utilizes Terracing
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 80 Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.