What Is Half Of 750
cibeltiagestion
Sep 25, 2025 · 5 min read
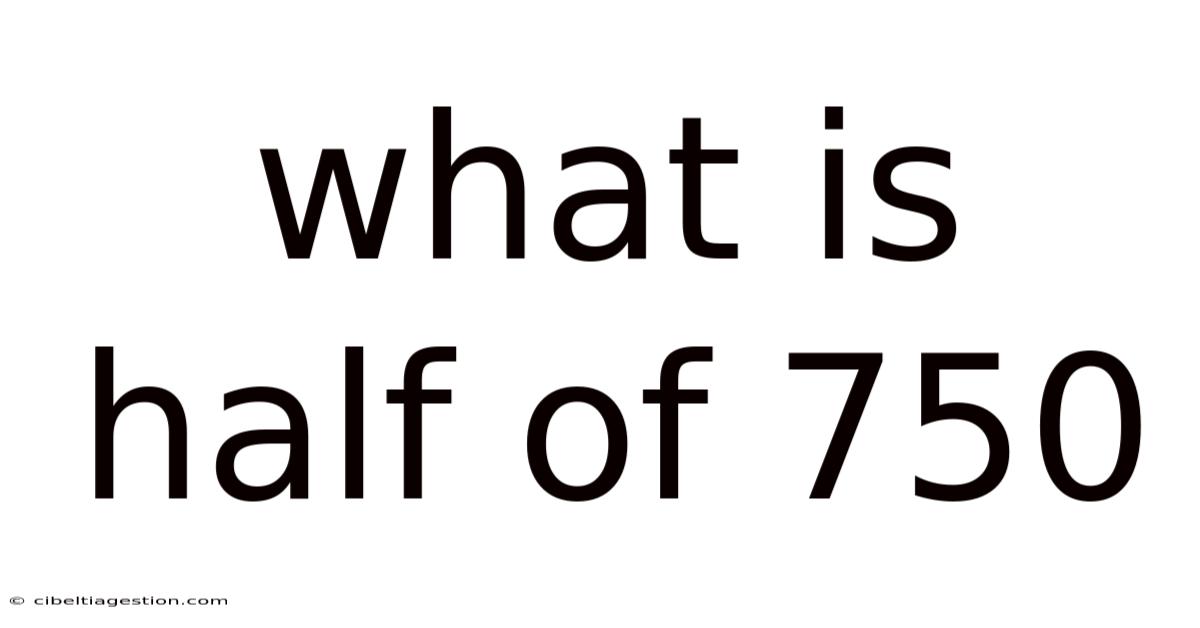
Table of Contents
What is Half of 750? A Deep Dive into Division and its Applications
Finding half of a number is a fundamental mathematical concept, crucial for everyday life and advanced calculations alike. This seemingly simple question, "What is half of 750?", opens the door to exploring various methods of division, understanding fractions, and appreciating the practical applications of these mathematical principles. This article will not only answer the question directly but also delve into the underlying mathematical concepts, explore different approaches to solving the problem, and discuss its relevance in various real-world scenarios.
Understanding the Concept of Halving
Before jumping into the calculation, let's establish a solid understanding of what "half" means. Half signifies one of two equal parts of a whole. When we say "half of 750," we're asking for the value of one part when 750 is divided into two equal portions. This is essentially a division problem: 750 divided by 2.
Methods to Calculate Half of 750
Several methods can effectively determine half of 750. We will explore the most common and intuitive approaches:
1. Direct Division:
The most straightforward method involves directly dividing 750 by 2. This can be done using various tools, from mental arithmetic to calculators.
-
Mental Calculation: We can break down 750 into smaller, more manageable numbers. Think of it as (700/2) + (50/2) = 350 + 25 = 375.
-
Calculator: A calculator provides the quickest solution. Simply input "750 ÷ 2" and the answer, 375, will be displayed.
-
Long Division: For those who prefer a more manual approach, long division offers a step-by-step breakdown of the process:
375
2 | 750
-6
15
-14
10
-10
0
2. Using Fractions:
Half can be represented as the fraction 1/2. Therefore, finding half of 750 is equivalent to calculating (1/2) * 750. This involves multiplying 750 by the numerator (1) and then dividing by the denominator (2):
(1/2) * 750 = 750/2 = 375
3. Repeated Subtraction:
While less efficient for larger numbers, repeated subtraction demonstrates the concept of halving. Continuously subtract 2 from 750 until you reach 0. The number of times you subtract 2 will be half of 750. While practical for smaller numbers, this becomes cumbersome for larger ones.
The Answer: 375
Regardless of the method employed, the answer remains consistent: half of 750 is 375.
Practical Applications of Halving
The seemingly simple act of finding half of a number has numerous practical applications across diverse fields:
-
Everyday Life: Sharing items equally amongst two people, calculating discounts (50% off), splitting bills, or measuring ingredients for cooking recipes all involve halving.
-
Business and Finance: Calculating profit margins, dividing resources, determining the average of two values, and splitting investments are common financial applications.
-
Engineering and Design: Halving dimensions is essential in scaling down designs, creating symmetrical structures, and calculating material requirements.
-
Computer Science: Binary systems, which form the foundation of modern computing, heavily rely on halving and doubling. Data compression techniques and algorithm design often utilize this concept.
Expanding the Understanding: Beyond Halving
Understanding halving helps build a foundation for understanding other fractional parts and proportions. For example:
-
Finding a quarter (1/4): Halving the result of halving 750 (375/2 = 187.5) gives you a quarter of 750.
-
Finding three-quarters (3/4): Multiplying the result of halving 750 (375) by 1.5 or adding half of 750 to a quarter of 750 will give you three-quarters of 750 (375 x 1.5 = 562.5).
-
Finding other fractions: The same principle applies to other fractions; you can express them as decimals and multiply them by the original number.
Mathematical Principles Involved:
The calculation of half of 750 touches upon several core mathematical principles:
-
Division: The most direct approach involves dividing 750 by 2.
-
Fractions: Representing half as 1/2 allows us to express the problem as a fraction multiplication.
-
Proportions: Halving implies a ratio of 1:2, signifying that one part is half the size of the whole.
-
Decimals: Depending on the method used, decimals might arise, reinforcing the relationship between fractions and decimal representation.
Frequently Asked Questions (FAQ)
-
Q: What if I want to find more than half of 750?
- A: If you need to find a different fraction or percentage of 750, convert the percentage to a decimal and multiply by 750. For example, to find 75% of 750, multiply 750 by 0.75 (750 * 0.75 = 562.5).
-
Q: Can I use this method for numbers with decimals?
- A: Yes, absolutely. The same principles apply to numbers with decimals. For example, to find half of 750.5, you would divide 750.5 by 2 (750.5/2 = 375.25).
-
Q: What if the number is not easily divisible by 2?
- A: Even if the number doesn't divide evenly by 2, you can still find half by using decimal representation. For example, half of 751 is 375.5.
-
Q: Are there other ways to visualize halving?
- A: Yes, you can use diagrams, charts, or even physical objects to represent halving. Dividing a circle in half, for instance, is a visual way to demonstrate the concept.
Conclusion
Finding half of 750, although seemingly simple, offers a gateway to a deeper understanding of fundamental mathematical principles. This seemingly basic calculation lays the groundwork for understanding division, fractions, proportions, and their diverse applications in numerous real-world scenarios. By mastering this fundamental concept, we equip ourselves with valuable skills applicable across various fields, from everyday tasks to advanced scientific and engineering pursuits. Remembering that half of 750 is 375 is just the beginning of a much broader mathematical journey.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is Half Of 750 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.