What Times What Equals 15
cibeltiagestion
Sep 08, 2025 · 6 min read
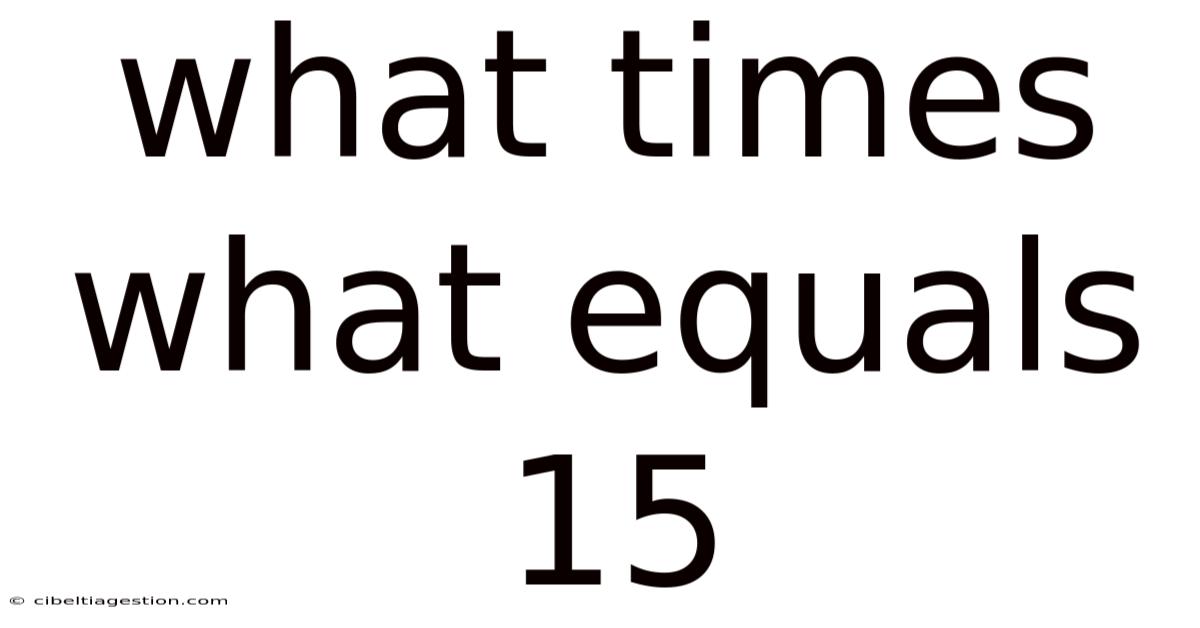
Table of Contents
What Times What Equals 15? Exploring Factor Pairs and Number Theory
Finding the numbers that, when multiplied, equal 15 might seem like a simple arithmetic problem. However, delving into this seemingly straightforward question opens up a fascinating world of number theory, exploring concepts like factors, prime numbers, and even the elegance of mathematical relationships. This article will not only answer the initial question but will also delve deeper into the underlying mathematical principles involved, making it a valuable resource for anyone curious about the building blocks of mathematics.
Understanding Factors and Factor Pairs
The core concept here revolves around factors. Factors are numbers that divide evenly into another number without leaving a remainder. In our case, we're looking for factor pairs of 15 – two numbers that, when multiplied together, result in 15.
Let's systematically explore the possibilities:
- 1 x 15 = 15: One and fifteen are a factor pair. One is a factor of every number, and 15 is, of course, a factor of itself.
- 3 x 5 = 15: Three and five are another factor pair. These are also important because they are prime numbers.
Therefore, the answer to "What times what equals 15?" is: 1 and 15, and 3 and 5. These are all the possible integer factor pairs.
Prime Factorization: The Building Blocks of Numbers
The factor pair of 3 and 5 is particularly significant because both 3 and 5 are prime numbers. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Prime numbers are the fundamental building blocks of all other whole numbers.
The process of breaking down a number into its prime factors is called prime factorization. For 15, the prime factorization is simply 3 x 5. This means that 15 cannot be broken down further into smaller prime number factors. Every whole number (except 1) has a unique prime factorization. This unique factorization is a cornerstone of number theory.
Let's consider a slightly more complex example: What times what equals 30? The factor pairs are numerous: 1 x 30, 2 x 15, 3 x 10, 5 x 6. However, the prime factorization of 30 is 2 x 3 x 5. Notice how all the other factor pairs are simply combinations of these prime factors.
Expanding the Search: Negative Factors
So far, we’ve only considered positive whole numbers. However, multiplication also works with negative numbers. Remember that a negative number multiplied by a negative number yields a positive result. Therefore, we can also include negative factor pairs for 15:
- -1 x -15 = 15
- -3 x -5 = 15
These add to our complete list of factor pairs for 15.
Beyond Whole Numbers: Rational and Irrational Factors
Our exploration thus far has focused on whole numbers, or integers. However, the concept of factors extends to rational numbers (numbers that can be expressed as a fraction of two integers) and even irrational numbers (numbers that cannot be expressed as a simple fraction, such as π or √2).
While finding rational factor pairs for 15 that aren't whole numbers is less straightforward and often involves fractions, it's still mathematically valid. For example, (1/2) x 30 = 15.
Irrational factors for 15 are less intuitive and often involve more advanced mathematical concepts. It’s not easily demonstrable in a simple format.
Applications in Algebra and Beyond
Understanding factors is crucial in various areas of mathematics, particularly algebra. Factoring is a fundamental technique used to solve equations, simplify expressions, and analyze mathematical relationships. For example, when solving a quadratic equation, factoring often provides a direct path to the solution.
Consider the simple quadratic equation x² - 8x + 15 = 0. Factoring the quadratic expression gives us (x - 3)(x - 5) = 0. This directly leads to the solutions x = 3 and x = 5. The factors of 15 become integral to finding the roots of the equation.
The importance of factors extends beyond basic algebra. They are applied in cryptography, computer science (particularly in algorithms), and various areas of engineering.
Further Exploration: The Divisibility Rules
Learning divisibility rules can help quickly determine if a number is divisible by a specific integer without performing the actual division. For instance:
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3. Since 1 + 5 = 6, and 6 is divisible by 3, we know 15 is divisible by 3.
- Divisibility by 5: A number is divisible by 5 if its last digit is either 0 or 5. Since 15 ends in 5, it's divisible by 5.
These rules are useful for quickly identifying potential factors, particularly when dealing with larger numbers.
Frequently Asked Questions (FAQ)
Q: Are there any other numbers besides 1, 3, 5, and 15 (and their negatives) that multiply to 15?
A: No, there aren't any other integer factors. However, as discussed, there are rational and irrational numbers which, when multiplied, could equal 15, but these are beyond the scope of simple whole number multiplication.
Q: How can I find the factors of larger numbers?
A: For larger numbers, systematic methods are crucial. One approach is to start by dividing the number by the smallest prime numbers (2, 3, 5, 7, and so on) until you find a prime factor. Then, continue factoring the remaining quotient until you have only prime numbers. This is essentially the prime factorization method.
Q: What is the significance of prime factorization in mathematics?
A: Prime factorization is fundamental because it provides a unique representation of any whole number. It's used extensively in number theory, cryptography, and other areas of mathematics. The uniqueness of prime factorization is a cornerstone of many mathematical theorems and proofs.
Q: How can I improve my understanding of factors and multiplication?
A: Practice is key! Work through various multiplication problems, try factoring different numbers, and challenge yourself with more complex problems. Online resources, textbooks, and educational games can provide plenty of practice opportunities.
Conclusion: The Enduring Importance of Simple Arithmetic
While the question "What times what equals 15?" may seem elementary, it serves as a powerful starting point for understanding fundamental mathematical concepts like factors, prime factorization, and number theory. Mastering these concepts is essential not only for academic success but also for developing a deeper appreciation of the elegance and interconnectedness of mathematics. This seemingly simple arithmetic problem opens a gateway to a much larger and fascinating world of mathematical exploration. The exploration of factors is not just about finding the answer; it's about understanding the underlying mathematical principles and their far-reaching implications.
Latest Posts
Latest Posts
-
Given The Graphed Function Below
Sep 08, 2025
-
Simplify Mc001 1 Jpg Mc001 2 Jpg Mc001 3 Jpg Mc001 4 Jpg
Sep 08, 2025
-
Myplate Was Created To
Sep 08, 2025
-
3 3 5 As A Decimal
Sep 08, 2025
-
8 6 As A Mixed Number
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.