What Times What Equals 20
cibeltiagestion
Sep 15, 2025 · 6 min read
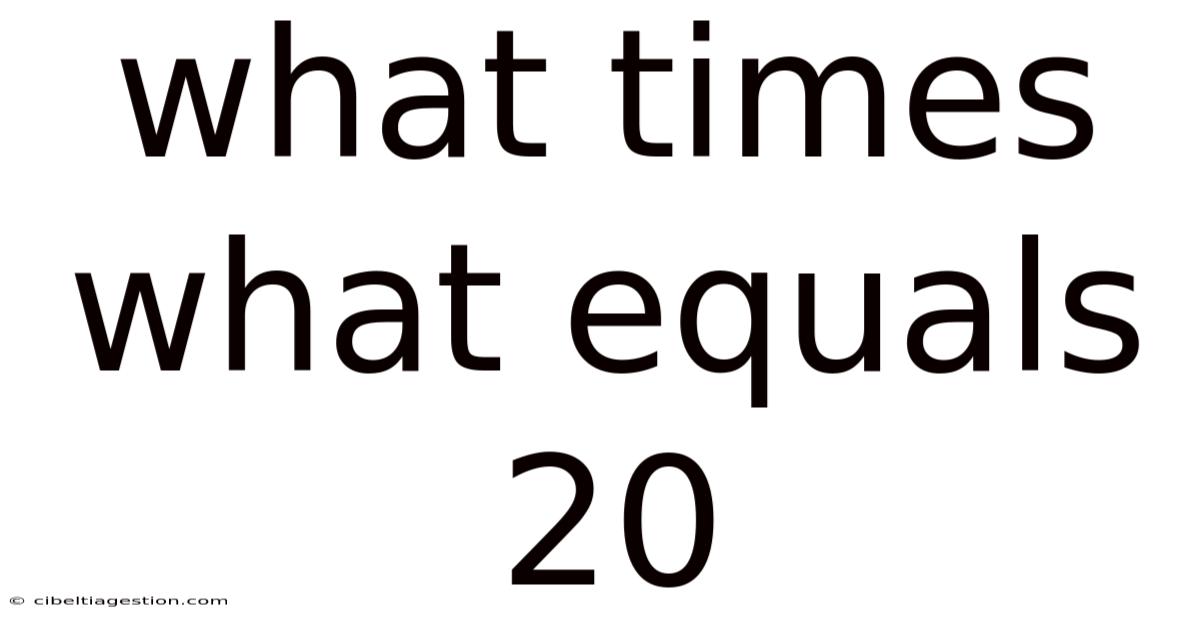
Table of Contents
What Times What Equals 20? Exploring the Factors and Applications of Multiplication
Finding the numbers that, when multiplied, equal 20 might seem like a simple elementary school math problem. However, this seemingly straightforward question opens a door to a deeper understanding of multiplication, factors, and their diverse applications across various fields. This article will explore the different pairs of numbers that multiply to 20, delve into the mathematical concepts behind this seemingly simple equation, and discuss its real-world relevance.
Introduction: Unveiling the Factors of 20
The question "What times what equals 20?" essentially asks us to find the factors of 20. Factors are numbers that divide evenly into another number without leaving a remainder. In simpler terms, they're the numbers that can be multiplied together to get the target number, in this case, 20. Understanding factors is crucial for various mathematical operations, including simplifying fractions, solving equations, and grasping more complex concepts like prime factorization.
Finding the Factor Pairs of 20:
Let's explore the different pairs of numbers that satisfy the equation:
-
1 x 20 = 20: This is the most obvious pair. One multiplied by any number always results in that number.
-
2 x 10 = 20: Two and ten are also factors of 20. This pair represents a smaller factor multiplied by a larger factor.
-
4 x 5 = 20: This pair shows two factors that are closer in value to each other.
These three pairs represent all the whole number factors of 20. Note that the order doesn't matter in multiplication (2 x 10 is the same as 10 x 2).
Expanding the Scope: Considering Negative Factors
While the question focuses on whole numbers, it's important to consider that negative numbers can also be involved. Remember, a negative number multiplied by a negative number results in a positive number. Therefore, we can also include these pairs:
- -1 x -20 = 20
- -2 x -10 = 20
- -4 x -5 = 20
These negative factor pairs are equally valid solutions to the equation "What times what equals 20?"
Delving Deeper: Prime Factorization and the Fundamental Theorem of Arithmetic
The concept of factors leads us to prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors. Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
The prime factorization of 20 is 2 x 2 x 5, often written as 2² x 5. This means that 20 can be constructed solely from the prime numbers 2 and 5. The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers. This theorem is foundational to many areas of number theory.
Real-World Applications: From Geometry to Finance
The seemingly simple equation "What times what equals 20?" has practical applications in various fields:
-
Geometry: Imagine you're designing a rectangular garden with an area of 20 square meters. Knowing the factors of 20 allows you to explore different possible dimensions for your garden (e.g., 1m x 20m, 2m x 10m, 4m x 5m).
-
Finance: Let's say you invest a certain amount of money, and after a period, your investment grows to $20,000. Knowing the factors of 20,000 can help you analyze different investment scenarios and growth rates. For instance, if your initial investment doubled five times (2 x 2 x 2 x 2 x 2 = 32), you may want to consider the effects of different investment strategies.
-
Data Analysis: Suppose you're analyzing data related to sales. If you have 20 items sold, understanding the factors helps you group or categorize the data for efficient analysis.
-
Everyday Life: Even simple tasks like arranging 20 items in rows or columns involve an understanding of factors. If you want to arrange 20 cookies evenly on a plate, the factors dictate how many rows and columns are possible.
Understanding the Concept of Multiplicative Identity
The number 1 plays a unique role in multiplication. It's the multiplicative identity, meaning that any number multiplied by 1 remains unchanged. This explains why 1 x 20 = 20. This property is fundamental to understanding how multiplication works.
Exploring Divisibility Rules
Understanding factors is closely related to divisibility rules. Divisibility rules are shortcuts for determining if a number is divisible by another number without performing the actual division. For 20, we can use the following divisibility rules:
- Divisible by 2: A number is divisible by 2 if it's an even number (ends in 0, 2, 4, 6, or 8). 20 is divisible by 2.
- Divisible by 4: A number is divisible by 4 if its last two digits are divisible by 4. The last two digits of 20 (20) are divisible by 4.
- Divisible by 5: A number is divisible by 5 if its last digit is 0 or 5. 20 is divisible by 5.
- Divisible by 10: A number is divisible by 10 if its last digit is 0. 20 is divisible by 10.
These divisibility rules help us quickly identify some of the factors of 20 without performing lengthy divisions.
Mathematical Extensions: Beyond Whole Numbers
The concept of factors extends beyond whole numbers. We can also explore rational numbers (fractions) and irrational numbers. For example:
-
Fractions: There are infinitely many pairs of fractions that multiply to 20. For instance, (1/2) x 40 = 20, (1/4) x 80 = 20, and so on.
-
Decimals: Similarly, there are countless pairs of decimal numbers that multiply to 20. For example, 2.5 x 8 = 20, 1.25 x 16 = 20.
This highlights the vastness of the mathematical landscape even when considering a seemingly simple equation like "What times what equals 20?"
Frequently Asked Questions (FAQ)
-
Q: Are there any other numbers besides the ones listed that multiply to 20? A: If we restrict ourselves to whole numbers, the pairs listed above are all the possibilities. However, if we include fractions and decimals, there are infinitely many solutions.
-
Q: How can I find factors of larger numbers? A: For larger numbers, systematic methods like prime factorization and divisibility rules become crucial. You can also use factor trees to visualize the process of breaking down a number into its prime factors.
-
Q: What is the significance of prime factorization? A: Prime factorization is a cornerstone of number theory. It forms the basis for various algorithms in cryptography, computer science, and other fields.
Conclusion: The Power of Simple Math
The question "What times what equals 20?" might seem elementary, but its exploration reveals a wealth of mathematical concepts and real-world applications. From understanding factors and prime factorization to applying these concepts in geometry, finance, and data analysis, this simple equation unveils the interconnectedness of different mathematical ideas and their significance in our daily lives. It highlights the power of seemingly simple mathematical problems to unlock a deeper understanding of the world around us. Remember, even simple questions can lead to fascinating discoveries, encouraging continued exploration and learning in the fascinating world of mathematics.
Latest Posts
Latest Posts
-
What Is A Collective Farm
Sep 15, 2025
-
How Do You Spell Yawn
Sep 15, 2025
-
How Long Is 90 Mins
Sep 15, 2025
-
Chemical Formula For Lithium Nitrate
Sep 15, 2025
-
Keegan Is A Police Officer
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.