What Times What Equals 7
cibeltiagestion
Sep 10, 2025 · 6 min read
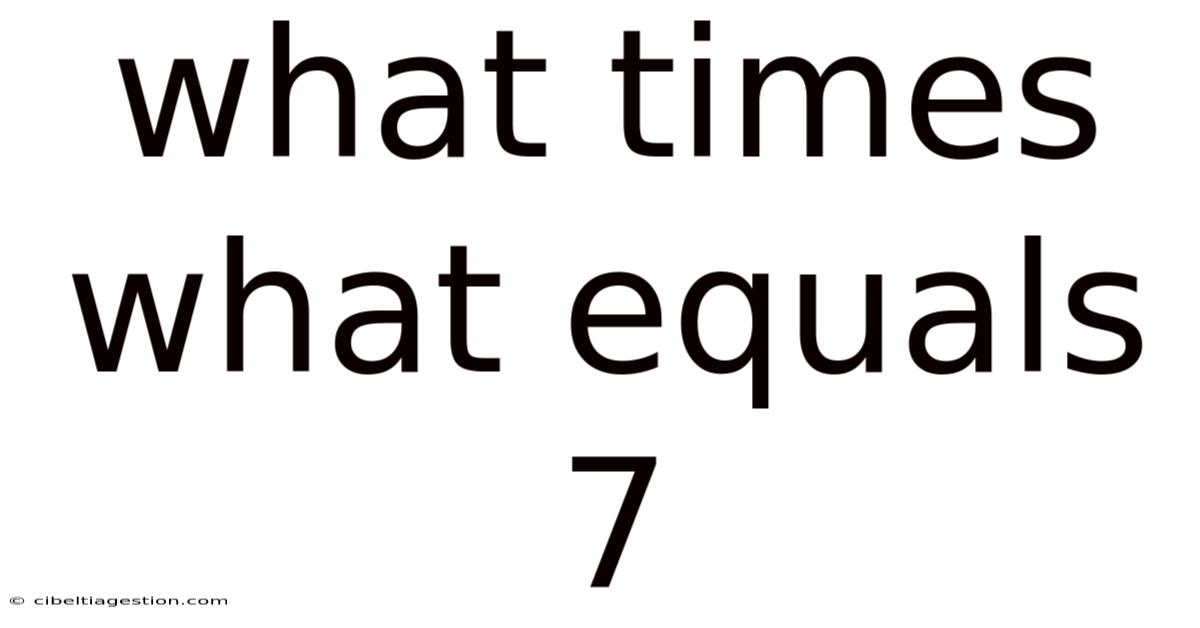
Table of Contents
What Times What Equals 7? Exploring the Multiplicative Landscape of Seven
Finding two whole numbers that multiply to equal 7 might seem like a simple problem, but it opens a door to a surprisingly rich exploration of mathematical concepts. This seemingly straightforward question delves into the properties of prime numbers, factors, and the broader world of multiplication and number theory. Let's unpack this seemingly simple question and reveal its hidden mathematical depths.
Introduction: The Uniqueness of Seven
The immediate answer to "what times what equals 7?" is 1 x 7 = 7 and 7 x 1 = 7. However, this simple solution belies a deeper truth about the number 7. Seven is a prime number, meaning it's a whole number greater than 1 that has only two divisors: 1 and itself. This characteristic is what makes its multiplicative possibilities limited to these two pairs. Unlike composite numbers (like 12, which can be factored as 2 x 6, 3 x 4, and 2 x 2 x 3), 7's prime nature restricts its factorization. Understanding this property is crucial to grasping the uniqueness of this problem.
Exploring Factors and Divisors
The question, "what times what equals 7?", essentially asks us to find the factors of 7. Factors are numbers that divide evenly into a given number without leaving a remainder. In the case of 7, the only factors are 1 and 7. These factors are also known as divisors. The number 7 has only two divisors, further emphasizing its prime nature. This contrasts sharply with composite numbers, which possess multiple pairs of factors.
For example, let's consider the number 12:
- 1 x 12 = 12
- 2 x 6 = 12
- 3 x 4 = 12
The number 12 has six factors: 1, 2, 3, 4, 6, and 12. This illustrates the difference between prime and composite numbers in terms of their factor count.
The Significance of Prime Numbers
Prime numbers, like 7, form the fundamental building blocks of all whole numbers. This is due to the Fundamental Theorem of Arithmetic, which states that every whole number greater than 1 can be expressed uniquely as a product of prime numbers (ignoring the order of the factors). This theorem highlights the importance of prime numbers in number theory. They are the indivisible atoms of the number system. Understanding prime numbers is critical in areas like cryptography, where their unique properties are leveraged to secure digital information.
The search for prime numbers, their distribution, and their properties has captivated mathematicians for centuries. The quest for larger and larger prime numbers continues to this day, driven both by intellectual curiosity and practical applications in cryptography and computer science.
Beyond Whole Numbers: Expanding the Possibilities
Our initial answer focused on whole numbers. However, if we expand our search beyond the realm of integers, we open up a wider range of possibilities. For instance:
-
Fractions: We could express 7 as a product of fractions. For example, (1/2) x 14 = 7, or (2/3) x (21/2) = 7. Infinitely many fractional pairs could yield a product of 7.
-
Decimals: Similarly, we can use decimals: 0.5 x 14 = 7, 0.1 x 70 = 7, and so on. Again, the possibilities are virtually limitless.
-
Negative Numbers: We could also include negative numbers: (-1) x (-7) = 7. This introduces the concept of multiplying two negative numbers to obtain a positive result.
The choice to restrict our search to whole numbers significantly constrained the solution set. By widening our scope, we unveil a much richer and more complex multiplicative landscape.
The Concept of Multiplicative Inverses
When working with fractions and decimals, the concept of multiplicative inverse (or reciprocal) becomes relevant. The multiplicative inverse of a number is the number that, when multiplied by the original number, yields 1. For example, the multiplicative inverse of 7 is 1/7, because 7 x (1/7) = 1. This concept is fundamental in algebra and is used extensively in solving equations and simplifying expressions.
The multiplicative inverse helps us to understand how different numbers relate to each other in multiplication. It provides another perspective on the multiplicative landscape surrounding the number 7.
Applications of Multiplication and Prime Numbers
The seemingly simple question, "what times what equals 7?", touches upon fundamental concepts that have wide-ranging applications. Here are some examples:
-
Cryptography: As mentioned earlier, prime numbers play a crucial role in modern cryptography. Algorithms like RSA encryption rely heavily on the difficulty of factoring large composite numbers into their prime components.
-
Computer Science: Prime numbers are used in various algorithms for hashing, data structures, and random number generation.
-
Number Theory: The study of prime numbers is a central theme in number theory, a branch of mathematics that explores the properties and relationships of numbers.
-
Coding Theory: Prime numbers have applications in error detection and correction codes.
-
Data Compression: Prime factorization can be used in specific types of data compression algorithms.
These examples demonstrate the far-reaching implications of concepts seemingly limited to a simple arithmetic problem.
Frequently Asked Questions (FAQ)
Q: Are there any other whole numbers that, when multiplied, equal 7?
A: No, 7 is a prime number, meaning its only whole number factors are 1 and itself. Therefore, the only whole number pairs that multiply to 7 are 1 x 7 and 7 x 1.
Q: What if I use negative numbers?
A: If you include negative numbers, then (-1) x (-7) = 7 is also a valid solution.
Q: How does this relate to other mathematical concepts?
A: This question touches upon prime numbers, factorization, the Fundamental Theorem of Arithmetic, and the concept of multiplicative inverses. These concepts are fundamental to various branches of mathematics, including number theory, algebra, and cryptography.
Q: Why is 7 considered a prime number?
A: A prime number is a whole number greater than 1 that is only divisible by 1 and itself. 7 satisfies this definition, as it's only divisible by 1 and 7.
Q: Are there infinitely many prime numbers?
A: Yes, this has been proven mathematically. Euclid's proof of the infinitude of primes is a classic demonstration of this fundamental fact in number theory.
Conclusion: Beyond the Obvious
The seemingly trivial question, "what times what equals 7?", offers a surprisingly deep dive into the world of mathematics. From the fundamental nature of prime numbers to their widespread applications in various fields, this seemingly simple problem illuminates the interconnectedness of mathematical concepts and the power of seemingly simple numbers. The seemingly simple answer masks a wealth of underlying mathematical richness, illustrating the power of exploration and the surprising depths that lie within even the most elementary arithmetic problems. The exploration of this question should inspire a curiosity for further investigation into the fascinating world of numbers and their properties.
Latest Posts
Latest Posts
-
Did Rockefeller Use Horizontal Integration
Sep 10, 2025
-
1 10 Is Equivalent To
Sep 10, 2025
-
Noble Gas Configuration For Mercury
Sep 10, 2025
-
Defg Is An Isosceles Trapezoid
Sep 10, 2025
-
How Are New Viruses Made
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.