What's 2 3 Times 2
cibeltiagestion
Sep 13, 2025 · 5 min read
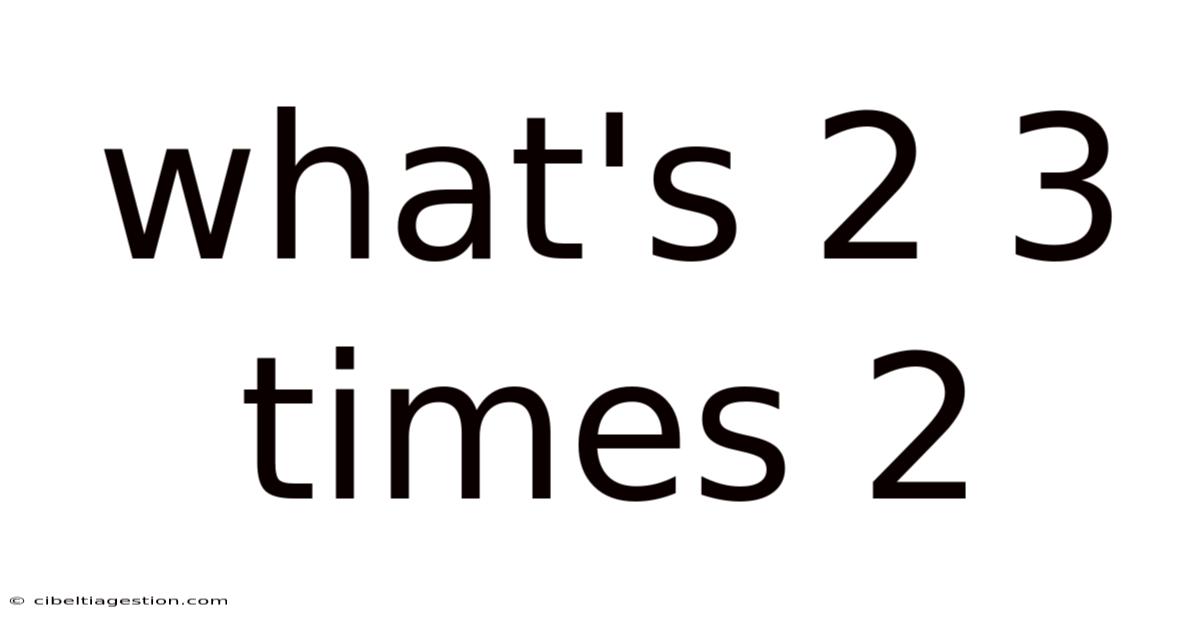
Table of Contents
What's 2/3 Times 2? Understanding Fractions and Multiplication
This seemingly simple question, "What's 2/3 times 2?", opens a door to a fundamental concept in mathematics: multiplying fractions. Understanding this not only solves this specific problem but builds a strong foundation for more complex mathematical operations. This article will guide you through the process, explaining the underlying principles, providing different approaches to solve the problem, and exploring related concepts to enhance your understanding of fractions and multiplication.
Understanding Fractions: A Quick Refresher
Before tackling the multiplication, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 2/3, the numerator is 2, and the denominator is 3. This means we have 2 parts out of a total of 3 equal parts.
Method 1: Visual Representation
One of the best ways to understand fraction multiplication is through visualization. Let's represent 2/3 using a simple diagram. Imagine a rectangle divided into three equal parts. Shade two of these parts to represent 2/3.
Now, we want to find 2/3 * 2. This means we want to double the amount we already have. So, we'll take another identical rectangle, also divided into three equal parts and shade two parts again.
By combining the shaded areas from both rectangles, we have a total of four shaded parts out of a possible six. This visually represents 4/6. This fraction can be simplified to 2/3 by dividing both the numerator and the denominator by their greatest common divisor, which is 2. Therefore, 2/3 * 2 = 4/6 = 2/3.
Method 2: Multiplying the Numerator
A more direct method involves multiplying the numerator of the fraction by the whole number. In our problem, 2/3 * 2, we multiply the numerator (2) by 2, keeping the denominator unchanged. This gives us:
(2 * 2) / 3 = 4/3
This is an improper fraction, meaning the numerator is larger than the denominator. We can convert this improper fraction into a mixed number. A mixed number combines a whole number and a proper fraction. To do this, we divide the numerator (4) by the denominator (3):
4 ÷ 3 = 1 with a remainder of 1.
This means 4/3 is equal to 1 and 1/3.
Method 3: Converting to Decimal
Another approach involves converting the fraction to its decimal equivalent before multiplying. To convert 2/3 to a decimal, we divide the numerator by the denominator:
2 ÷ 3 ≈ 0.6667 (repeating decimal)
Now, we multiply this decimal by 2:
0.6667 * 2 ≈ 1.3334
This decimal value is approximately equal to 1 and 1/3, confirming our previous results. It's important to note that using decimals can introduce slight inaccuracies due to rounding, especially with repeating decimals. Therefore, working with fractions is generally preferred for accuracy.
The Mathematical Principle Behind Fraction Multiplication
The core principle behind multiplying a fraction by a whole number is straightforward. We are essentially adding the fraction to itself a certain number of times. In our example, 2/3 * 2 means adding 2/3 to itself twice:
2/3 + 2/3 = 4/3
Notice that when adding fractions with the same denominator, we simply add the numerators and keep the denominator the same. This is consistent with the method of multiplying the numerator by the whole number.
Extending the Concept: Multiplying Two Fractions
The principle of multiplying fractions extends beyond multiplying a fraction by a whole number. Let's consider multiplying two fractions, for instance, 2/3 * 1/2. In this case, we multiply the numerators together and the denominators together:
(2 * 1) / (3 * 2) = 2/6
This fraction can be simplified to 1/3 by dividing both the numerator and the denominator by 2.
Solving Similar Problems
Let's practice applying these methods to similar problems:
-
What is 3/4 times 3? Using the method of multiplying the numerator, we get (3 * 3) / 4 = 9/4 = 2 1/4. Visual representation would involve three rectangles, each divided into four parts, with three parts shaded in each.
-
What is 1/5 times 4? This equals (1 * 4) / 5 = 4/5.
-
What is 2/5 times 3/4? Multiplying the numerators and the denominators, we get (2 * 3) / (5 * 4) = 6/20. This simplifies to 3/10.
Frequently Asked Questions (FAQs)
Q: Why can't I just multiply the whole numbers and then the fractions separately?
A: You cannot simply multiply the whole numbers and the fractions separately because the multiplication of fractions represents a different kind of operation than the multiplication of whole numbers. It involves scaling a portion of a whole, not just adding whole units.
Q: What if I have a mixed number instead of a whole number?
A: If you are multiplying a fraction by a mixed number, first convert the mixed number into an improper fraction. Then, multiply the numerators and denominators as described earlier. For example, to calculate 2/3 x 1 1/2, convert 1 1/2 to 3/2. Then multiply 2/3 x 3/2 = 6/6 =1.
Q: What are some real-world applications of fraction multiplication?
A: Fraction multiplication is used in countless real-world situations. For example, calculating cooking recipes (e.g., halving a recipe), determining discounts (e.g., finding 2/3 off an item's price), measuring materials (e.g., determining the amount of fabric needed for a project), and many more.
Conclusion
The seemingly simple question, "What's 2/3 times 2?", provides a valuable opportunity to reinforce our understanding of fractions and multiplication. Through various methods—visual representation, direct multiplication, and decimal conversion—we've demonstrated that 2/3 times 2 equals 4/3 or 1 and 1/3. This understanding extends beyond this specific problem to more complex fraction operations and real-world applications. Mastering fraction multiplication is a cornerstone of mathematical proficiency and opens doors to solving a vast array of problems. Remember to practice regularly to solidify your understanding and build confidence in your mathematical skills. The more you practice, the more intuitive these concepts will become.
Latest Posts
Latest Posts
-
How Many Days In March
Sep 13, 2025
-
14 Degrees F To C
Sep 13, 2025
-
Demand Rate For Transcutaneous Pacer
Sep 13, 2025
-
Who Won The 1824 Election
Sep 13, 2025
-
What Aisle Is Cornstarch In
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What's 2 3 Times 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.