X 2 2x 8 0
cibeltiagestion
Sep 15, 2025 · 5 min read
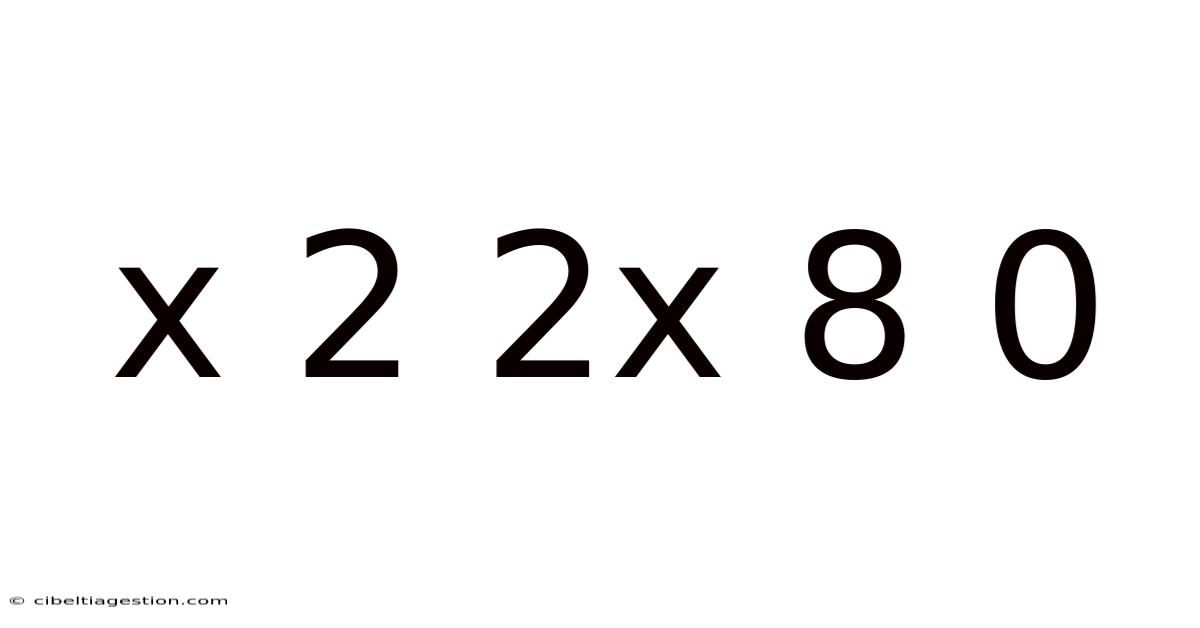
Table of Contents
Decoding the Mystery: x 2 2x 8 0 – A Deep Dive into Algebraic Equations
This article explores the meaning and solution of the cryptic sequence "x 2 2x 8 0". This seemingly simple string of numbers and letters actually represents a quadratic equation, a fundamental concept in algebra. We will unravel this equation, understand its components, and solve it using various methods, making the process clear and accessible even for those with limited mathematical backgrounds. We'll also delve into the practical applications of quadratic equations and answer frequently asked questions.
Understanding the Equation: Breaking Down the Basics
The sequence "x 2 2x 8 0" is a shorthand representation of a quadratic equation. Let's break it down piece by piece:
-
x: This represents an unknown variable, a value we need to find. Think of it as a puzzle piece we're trying to fit into place.
-
2: This is the coefficient of the x² term. It tells us how many times x² is included in the equation.
-
2x: This is the linear term, containing the variable x raised to the power of 1. The coefficient is 2.
-
8: This is the constant term, a number without a variable.
-
0: This indicates that the entire expression equals zero. This is crucial because it means we're looking for the values of 'x' that make the entire equation true.
Putting it all together, the complete equation is written as: x² + 2x - 8 = 0
This is a standard form of a quadratic equation, represented generally as: ax² + bx + c = 0, where 'a', 'b', and 'c' are constants. In our case, a = 1, b = 2, and c = -8.
Methods for Solving Quadratic Equations
There are several methods to solve quadratic equations. We'll explore three common techniques: factoring, using the quadratic formula, and completing the square.
1. Factoring: A Simple Approach
Factoring involves breaking down the quadratic expression into two simpler expressions that multiply together to give the original. This method is efficient when the factors are easily identifiable.
To factor x² + 2x - 8 = 0, we look for two numbers that add up to 2 (the coefficient of x) and multiply to -8 (the constant term). These numbers are 4 and -2. Therefore, we can rewrite the equation as:
(x + 4)(x - 2) = 0
This means either (x + 4) = 0 or (x - 2) = 0. Solving these simple equations gives us:
- x = -4
- x = 2
These are the two solutions (or roots) of the quadratic equation.
2. The Quadratic Formula: A Universal Solution
The quadratic formula is a powerful tool that works for all quadratic equations, regardless of whether they are easily factorable or not. The formula is derived from completing the square method and is given by:
x = [-b ± √(b² - 4ac)] / 2a
Substituting the values from our equation (a = 1, b = 2, c = -8), we get:
x = [-2 ± √(2² - 4 * 1 * -8)] / (2 * 1) x = [-2 ± √(4 + 32)] / 2 x = [-2 ± √36] / 2 x = [-2 ± 6] / 2
This gives us two solutions:
- x = (-2 + 6) / 2 = 4 / 2 = 2
- x = (-2 - 6) / 2 = -8 / 2 = -4
As you can see, we arrive at the same solutions as with the factoring method.
3. Completing the Square: A Step-by-Step Approach
Completing the square is a method that transforms the quadratic equation into a perfect square trinomial, making it easier to solve. It's a more methodical approach than factoring.
-
Move the constant term: Rewrite the equation as x² + 2x = 8
-
Complete the square: To complete the square for x² + 2x, take half of the coefficient of x (which is 2/2 = 1), square it (1² = 1), and add it to both sides of the equation:
x² + 2x + 1 = 8 + 1 x² + 2x + 1 = 9
- Factor the perfect square trinomial: The left side is now a perfect square trinomial:
(x + 1)² = 9
- Solve for x: Take the square root of both sides:
x + 1 = ±3
- Isolate x:
x = -1 ± 3
This gives us the two solutions:
- x = -1 + 3 = 2
- x = -1 - 3 = -4
Again, we obtain the same solutions. The choice of method depends on personal preference and the specific characteristics of the equation.
The Significance of Quadratic Equations
Quadratic equations are not just abstract mathematical concepts; they have significant real-world applications across various fields:
-
Physics: Calculating projectile motion, determining the trajectory of objects under gravity, and analyzing oscillations.
-
Engineering: Designing bridges, buildings, and other structures; optimizing shapes and dimensions for maximum strength and stability.
-
Economics: Modeling supply and demand, predicting market trends, and analyzing economic growth.
-
Computer Graphics: Creating curves and shapes in computer-generated images and animations.
-
Finance: Calculating compound interest, determining investment growth, and modeling financial scenarios.
Understanding and solving quadratic equations is therefore essential for anyone pursuing studies or careers in these fields.
Frequently Asked Questions (FAQ)
Q: What if the quadratic equation doesn't have real solutions?
A: Some quadratic equations have no real solutions. This happens when the discriminant (b² - 4ac) in the quadratic formula is negative. In such cases, the solutions are complex numbers involving the imaginary unit i (where i² = -1).
Q: Can a quadratic equation have only one solution?
A: Yes, a quadratic equation can have exactly one solution. This occurs when the discriminant (b² - 4ac) is equal to zero. The single solution is then given by x = -b / 2a.
Q: What is the difference between roots and solutions?
A: The terms "roots" and "solutions" are often used interchangeably in the context of quadratic equations. They both refer to the values of x that satisfy the equation.
Q: Are there other methods to solve quadratic equations?
A: Yes, there are other less common methods, such as using graphical techniques (plotting the parabola and finding its x-intercepts) or using numerical methods for equations that are difficult to solve analytically.
Conclusion
The seemingly simple sequence "x 2 2x 8 0" represents a powerful mathematical tool – the quadratic equation. Understanding this equation and its various solution methods is crucial for tackling more complex mathematical problems and applying these concepts to real-world situations. We’ve explored three common methods—factoring, the quadratic formula, and completing the square—demonstrating the versatility of approaches to solving this fundamental type of equation. Regardless of the chosen method, the ability to solve quadratic equations is a significant stepping stone in the journey of mathematical proficiency. Remember, the key is practice and understanding the underlying principles. So, keep practicing, and you'll master this essential algebraic skill in no time!
Latest Posts
Latest Posts
-
Square Root Of 40 Simplified
Sep 15, 2025
-
A 2 Person Relay Race
Sep 15, 2025
-
Increased Explicit Defence Modifier Magnitudes
Sep 15, 2025
-
What Is Half A Gallon
Sep 15, 2025
-
2 Copies Of 1 10 Is
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X 2 2x 8 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.