X 2 4 X 2
cibeltiagestion
Sep 06, 2025 · 6 min read
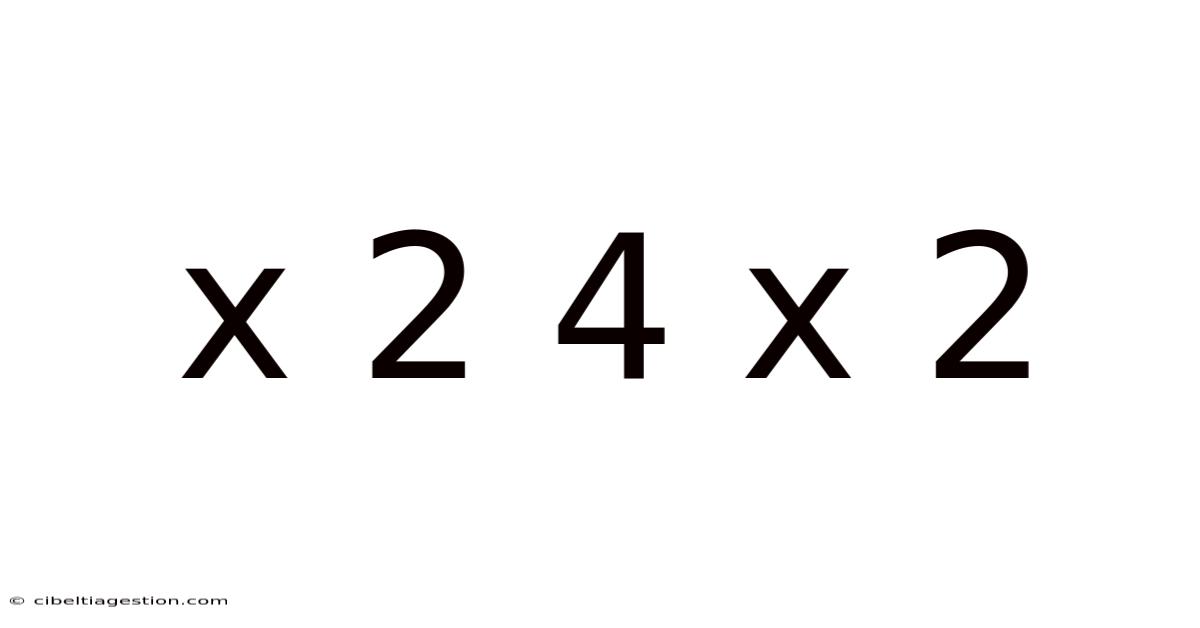
Table of Contents
Decoding the Mystery: A Deep Dive into X²4X²
The expression "x²4x²" might seem simple at first glance, but it opens a door to a fascinating world of algebraic manipulation, polynomial factorization, and problem-solving strategies. This article will unravel the complexities hidden within this seemingly straightforward expression, exploring its various interpretations, potential solutions, and applications in different mathematical contexts. We’ll delve into the core concepts, provide step-by-step explanations, and offer a comprehensive understanding suitable for both beginners and those seeking a deeper appreciation of algebraic principles.
Understanding the Fundamentals: What Does x²4x² Mean?
At its most basic level, "x²4x²" represents a mathematical expression involving a variable, x, raised to the power of 2 (squared), and a constant, 4, multiplied by x to the power of 2. The crucial element here is the interpretation – is this a single expression, a potential equation, or part of a larger problem? The meaning shifts depending on the context.
- As a Single Expression: The expression, without any equals sign (=), is simply a combination of terms. We can simplify it algebraically.
- As Part of an Equation: If the expression were part of an equation, such as "x²4x² = 0," we would be tasked with finding the value(s) of x that satisfy the equation. This would involve solving a quadratic equation.
- As a Polynomial: The expression can be viewed as a polynomial of degree 2, specifically a quadratic polynomial.
Simplifying the Expression: Algebraic Manipulation
The first step in understanding x²4x² is to simplify it. The expression likely suffers from a lack of explicit operators; a missing + or - sign between x² and 4x². Let’s assume two possibilities and solve them separately.
Scenario 1: x² + 4x²
This scenario assumes addition between the terms. The simplification is straightforward:
- Combine like terms: Since both terms contain x², we can add their coefficients: 1x² + 4x² = 5x²
Therefore, in this scenario, x² + 4x² simplifies to 5x².
Scenario 2: x² - 4x²
This scenario assumes subtraction between the terms. The simplification is equally straightforward:
- Combine like terms: Subtract the coefficients: 1x² - 4x² = -3x²
In this scenario, x² - 4x² simplifies to -3x².
Scenario 3: Interpreting as a Quadratic Equation: x² + 4x² = 0 or x² - 4x² = 0
If we treat x²4x² as part of an equation, like x² + 4x² = 0, or x² - 4x² = 0, then we can solve for x.
-
For x² + 4x² = 0: This simplifies to 5x² = 0. Dividing both sides by 5 gives x² = 0. Taking the square root of both sides yields x = 0. Therefore, x = 0 is the solution.
-
For x² - 4x² = 0: This simplifies to -3x² = 0. Dividing both sides by -3 gives x² = 0. Taking the square root of both sides again yields x = 0. Therefore, x = 0 is the solution.
Scenario 4: More Complex Interpretations and Implicit Multiplication
The expression could also be interpreted in more complex ways, particularly if we consider the possibility of implicit multiplication. For example, is there a missing multiplication sign between the 4 and x²?
If we interpret it as 4 * x² (4x²), the simplification depends on the context, as shown in the previous scenarios. However, it's crucial to use proper notation to avoid ambiguity. The lack of clear operators leads to multiple possible interpretations. This highlights the importance of precise mathematical notation.
Expanding on Quadratic Equations and their Solutions
The solutions obtained (x = 0 in scenarios 3) highlight the nature of quadratic equations. While many quadratic equations have two distinct solutions, the equations derived from interpreting x²4x² result in a single, repeated root. This is due to the specific form of these simplified equations (e.g., 5x² = 0 or -3x² = 0).
A standard quadratic equation is typically written as ax² + bx + c = 0, where a, b, and c are constants. The solutions are found using the quadratic formula:
x = [-b ± √(b² - 4ac)] / 2a
In our simplified scenarios (x² + 4x² = 0 and x² - 4x² = 0), the 'b' and 'c' terms are zero, leading to a simpler solution.
Delving Deeper: Factorization and Polynomial Properties
Understanding the concept of factorization is crucial when dealing with polynomials. Factorization is the process of breaking down an expression into smaller, simpler expressions that, when multiplied together, give the original expression.
In our simplified scenarios, 5x² can be factored as 5 * x * x. Similarly, -3x² can be factored as -3 * x * x.
The factorization process is particularly useful in solving quadratic equations. For instance, if we have a quadratic equation that can be factored easily, finding the solutions becomes much simpler.
Real-World Applications: Where Does This Matter?
While x²4x² might seem like an abstract concept, it has practical applications in various fields:
- Physics: Quadratic equations are used extensively in physics, particularly in projectile motion, where the trajectory of an object is described by a quadratic function.
- Engineering: Engineers use quadratic equations to model various phenomena, such as the strength of materials or the flow of fluids.
- Economics: Quadratic functions are used in economics to model various relationships, such as cost functions and revenue functions.
- Computer Graphics: Quadratic curves and surfaces are essential in computer graphics to create smooth and realistic shapes.
Frequently Asked Questions (FAQ)
-
Q: What does the "x²" mean?
- A: "x²" means "x squared" or "x to the power of 2," representing x multiplied by itself (x * x).
-
Q: What are the different ways to interpret x²4x²?
- A: The ambiguity arises from the missing operator between the terms. It can represent x² + 4x², x² - 4x², or potentially a more complex expression involving implicit multiplication.
-
Q: What is a polynomial?
- A: A polynomial is a mathematical expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents.
-
Q: What is the difference between a quadratic equation and a quadratic expression?
- A: A quadratic expression is simply an expression of degree 2 (highest power of the variable is 2), like 5x² or 3x² + 2x - 1. A quadratic equation is a quadratic expression set equal to zero (e.g., 5x² = 0 or 3x² + 2x - 1 = 0).
-
Q: How do I solve a quadratic equation?
- A: Quadratic equations can be solved using various methods, including factoring, the quadratic formula, and completing the square.
Conclusion: Mastering Algebraic Concepts
The seemingly simple expression "x²4x²" offers a valuable lesson in the importance of clear mathematical notation and the multiple interpretations that can arise from ambiguity. By exploring the different scenarios, simplifying the expression, and solving the resulting equations, we've gained a deeper understanding of algebraic manipulation, polynomial properties, and the broader applications of quadratic equations in various fields. Remember, precision in notation is key, and understanding the fundamental concepts will unlock a deeper appreciation for the power and versatility of algebra. This exercise emphasizes the crucial link between seemingly simple expressions and the rich mathematical world they represent.
Latest Posts
Latest Posts
-
What Marking Banner Or Footer
Sep 06, 2025
-
What Times What Equals 13
Sep 06, 2025
-
Abrasive Cleaners Cause Friction Which
Sep 06, 2025
-
How Many Electrons In Naf
Sep 06, 2025
-
If You Find Yourself Hydroplaning
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about X 2 4 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.