X 2 9x 2 0
cibeltiagestion
Sep 07, 2025 · 5 min read
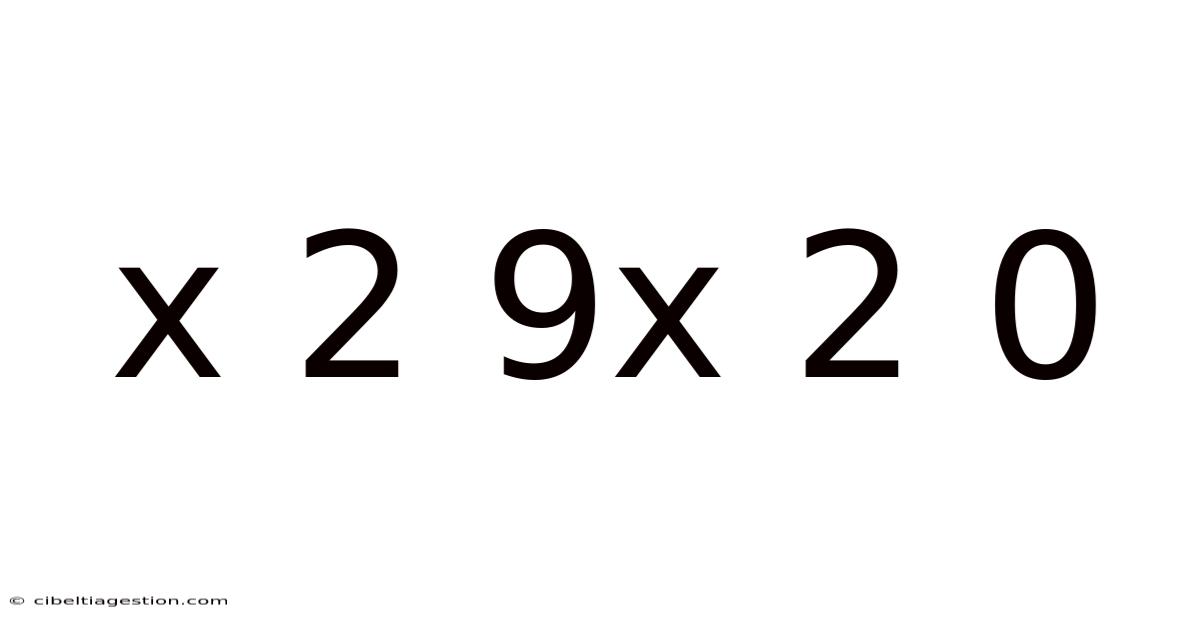
Table of Contents
Decoding the Enigma: Exploring the Mathematical Expression "x² + 9x² + 0"
This article delves into the seemingly simple, yet potentially multifaceted, mathematical expression "x² + 9x² + 0". While at first glance it appears straightforward, a deeper exploration reveals opportunities to understand fundamental algebraic principles, explore simplification techniques, and even touch upon more advanced concepts. This comprehensive guide will break down the expression step-by-step, catering to readers of various mathematical backgrounds, from beginners to those seeking a refresher.
Introduction: Understanding the Components
The expression "x² + 9x² + 0" consists of three terms:
-
x²: This represents a variable 'x' squared, meaning x multiplied by itself (x * x). It's a quadratic term because the highest power of the variable is 2.
-
9x²: This is another quadratic term, representing nine times x squared (9 * x * x). Note the coefficient '9' multiplying the x² term.
-
0: This is a constant term, representing the number zero. It has no impact on the overall value of the expression when simplified.
Understanding these individual components is crucial before attempting to simplify the entire expression.
Simplifying the Expression: Combining Like Terms
The core principle in simplifying this expression lies in combining like terms. Like terms are terms that have the same variable raised to the same power. In our case, both x² and 9x² are like terms. We can combine them by adding their coefficients:
1 + 9 = 10
Therefore, the simplified form of the expression becomes:
10x²
The constant term '0' doesn't contribute to the simplification as adding zero to any number doesn't change its value.
A Deeper Dive: Exploring the Underlying Principles
The simplification process highlights several fundamental algebraic concepts:
-
The Distributive Property: While not explicitly used in this particular simplification, the distributive property is essential for understanding how to manipulate similar expressions. For example, if the expression were 2(x² + 4.5x²), the distributive property allows us to expand it to 2x² + 9x², which is equivalent to our original expression before simplification.
-
Combining Coefficients: The ability to combine coefficients of like terms is a cornerstone of algebra. It demonstrates the power of factoring and recognizing common elements within algebraic expressions. This skill is crucial for solving equations, graphing functions, and performing more advanced mathematical operations.
-
The Concept of Zero: The presence of '0' in the original expression underscores the significance of the additive identity property. Adding zero to any number does not change its value. This seemingly simple concept underpins numerous mathematical operations and proofs.
Expanding the Scope: Applications and Further Exploration
While this specific expression might seem rudimentary, understanding its simplification lays a strong foundation for more complex algebraic manipulations. Consider these extensions:
-
Solving Quadratic Equations: Quadratic equations involve expressions with x² terms. The ability to simplify expressions like "x² + 9x² + 0" is essential for solving such equations using techniques like factoring, completing the square, or the quadratic formula.
-
Graphing Quadratic Functions: The simplified expression, 10x², represents a parabolic function. Understanding how to simplify the expression allows for easier graphing of this function and analyzing its properties, such as its vertex, axis of symmetry, and concavity.
-
Calculus: In calculus, the concept of derivatives and integrals involves manipulating and simplifying algebraic expressions. The foundational skills honed by simplifying "x² + 9x² + 0" are vital for performing these more advanced calculations.
-
Polynomial Operations: This expression demonstrates fundamental polynomial operations. Polynomials are expressions consisting of variables and coefficients, such as our example. The skills learned in simplifying this expression extend to adding, subtracting, multiplying, and dividing more complex polynomials.
Practical Examples: Real-World Applications
While the expression "x² + 9x² + 0" might not directly represent a tangible real-world scenario in its purest form, the underlying principles have numerous applications:
-
Area Calculations: Imagine calculating the area of two squares. One square has a side length of 'x', and the other has a side length of '3x'. The total area would be x² + (3x)² = x² + 9x² = 10x². This illustrates how simplifying similar expressions can be applied to geometry problems.
-
Physics and Engineering: Many physics and engineering problems involve quadratic equations and functions. Simplifying expressions like this is crucial for solving problems related to projectile motion, energy calculations, and structural analysis.
-
Financial Modeling: In finance, quadratic functions are sometimes used to model growth or decay. Understanding how to simplify expressions with quadratic terms is vital for analyzing financial models and making predictions.
Frequently Asked Questions (FAQ)
Q: Can I simplify the expression without combining like terms?
A: While technically you could leave the expression as is, combining like terms is the standard practice for simplifying algebraic expressions. It makes the expression more concise and easier to work with in further calculations.
Q: What if the expression was x² + 9x + 0 instead?
A: In that case, x² and 9x are not like terms because they have different powers of x. The expression would remain as x² + 9x. It cannot be further simplified unless more information is provided.
Q: What if the '0' was a different constant?
A: If the constant term was a number other than 0, it would not change the simplification of the x² terms. For example, x² + 9x² + 5 would simplify to 10x² + 5. The constant term would simply be added to the simplified expression.
Q: Is there a specific order of operations to follow?
A: In this instance, the order of operations isn’t strictly relevant because it involves only addition. However, understanding the order of operations (PEMDAS/BODMAS) is crucial for simplifying more complex expressions involving parentheses, exponents, multiplication, division, addition, and subtraction.
Conclusion: The Value of Simplicity
The seemingly uncomplicated mathematical expression "x² + 9x² + 0" offers a valuable opportunity to reinforce foundational algebraic concepts. By breaking down the expression, combining like terms, and exploring its underlying principles, we gain a deeper appreciation for the elegance and power of simplifying algebraic expressions. These foundational skills are not only crucial for succeeding in further mathematical studies but also provide a framework for problem-solving across various disciplines. The seemingly simple act of reducing "x² + 9x² + 0" to "10x²" exemplifies the beauty of mathematical precision and the importance of simplifying complexity to reveal underlying truths. The journey from a seemingly complex expression to its simplified form serves as a microcosm of the broader mathematical endeavor – the pursuit of clarity, precision, and elegant solutions.
Latest Posts
Latest Posts
-
Use Pious In A Sentence
Sep 07, 2025
-
Which Figures Demonstrate A Reflection
Sep 07, 2025
-
The Suns Observed Spectrum Is
Sep 07, 2025
-
What Is 40 Of 225
Sep 07, 2025
-
I Eat Apples In Spanish
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about X 2 9x 2 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.