X 3 3x 2 3
cibeltiagestion
Sep 08, 2025 · 6 min read
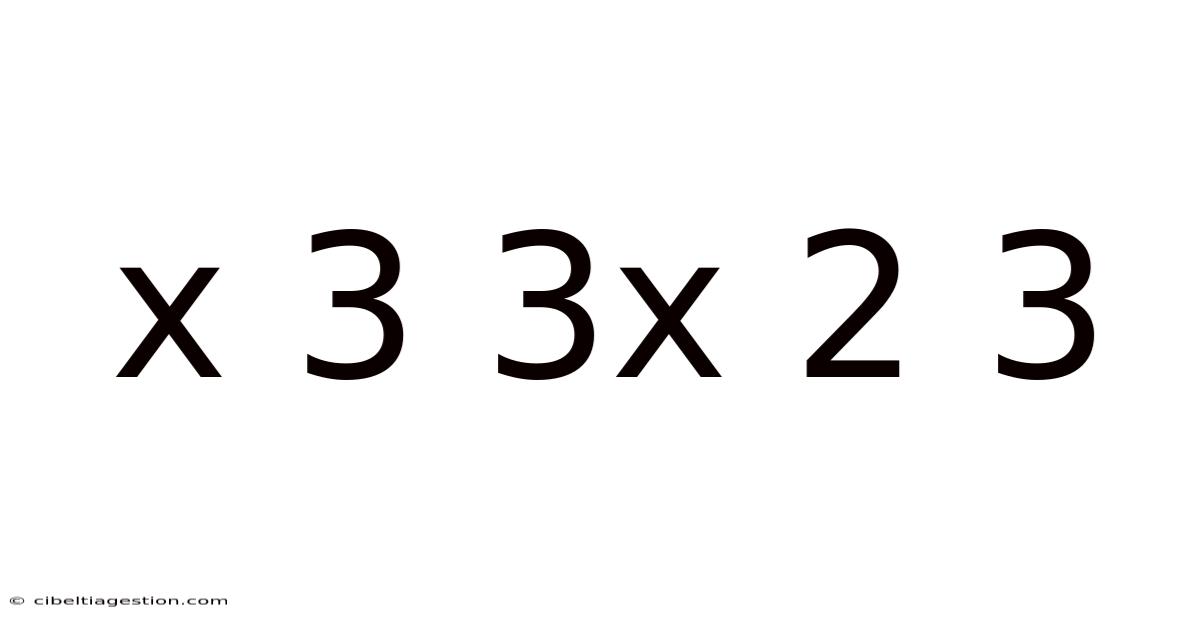
Table of Contents
Decoding the Mystery: Exploring the Mathematical Expression "x³ + 3x² + 3x + 1"
This article delves into the mathematical expression x³ + 3x² + 3x + 1, exploring its meaning, factorization, geometric interpretation, and practical applications. We'll unravel its secrets, step-by-step, making this complex topic accessible to everyone, regardless of their mathematical background. Understanding this expression opens doors to a deeper appreciation of algebra and its powerful applications.
Introduction: Unpacking the Polynomial
The expression x³ + 3x² + 3x + 1 is a polynomial – a mathematical expression involving variables and constants, combined using addition, subtraction, multiplication, and non-negative integer exponents. Specifically, it's a cubic polynomial because the highest power of the variable x is 3. This seemingly simple expression holds a wealth of mathematical significance and can be approached from several perspectives.
Factorization: Unveiling the Hidden Structure
One of the key aspects of understanding any polynomial is its factorization – breaking it down into simpler expressions that, when multiplied, yield the original polynomial. This is crucial for solving equations, simplifying expressions, and understanding its behavior. The factorization of x³ + 3x² + 3x + 1 is surprisingly elegant and reveals a fundamental pattern:
The expression is a perfect cube: it can be factored as (x + 1)³. This means (x + 1) multiplied by itself three times equals x³ + 3x² + 3x + 1. Let's verify this:
(x + 1)³ = (x + 1)(x + 1)(x + 1)
Expanding this using the distributive property (often referred to as FOIL for first, outer, inner, last):
(x + 1)(x + 1) = x² + 2x + 1
Then, multiplying this result by (x + 1) again:
(x² + 2x + 1)(x + 1) = x³ + x² + 2x² + 2x + x + 1 = x³ + 3x² + 3x + 1
This confirms our factorization. The ability to recognize and factor perfect cubes is a valuable skill in algebra.
The Binomial Theorem: A Deeper Understanding
The factorization of x³ + 3x² + 3x + 1 isn't just a coincidence. It's a direct consequence of the binomial theorem, a powerful tool for expanding expressions of the form (a + b)ⁿ, where 'n' is a positive integer. The binomial theorem states:
(a + b)ⁿ = Σ (nCk) * a^(n-k) * b^k (where k ranges from 0 to n)
Here, nCk represents the binomial coefficient, often written as "n choose k," which is the number of ways to choose k items from a set of n items. It's calculated as:
nCk = n! / (k! * (n-k)!)
where "!" denotes the factorial (e.g., 3! = 3 * 2 * 1 = 6).
In our case, (x + 1)³, we have a = x, b = 1, and n = 3. Applying the binomial theorem:
(x + 1)³ = 3C0 * x³ * 1⁰ + 3C1 * x² * 1¹ + 3C2 * x¹ * 1² + 3C3 * x⁰ * 1³
Calculating the binomial coefficients:
3C0 = 1 3C1 = 3 3C2 = 3 3C3 = 1
Substituting these values:
(x + 1)³ = 1 * x³ + 3 * x² + 3 * x + 1 = x³ + 3x² + 3x + 1
This demonstrates the direct link between the binomial theorem and the structure of our polynomial. This theorem is fundamental in various areas of mathematics, including probability and statistics.
Geometric Interpretation: Visualizing the Cube
The expression x³ + 3x² + 3x + 1 has a fascinating geometric interpretation. Recall that x³ represents the volume of a cube with side length x. The expression can be visualized as the volume of a larger cube constructed by adding layers to a smaller cube with side length x. Each term represents the volume of a different part of the larger cube:
- x³: The volume of the original cube with side length x.
- 3x²: The volume of three rectangular prisms, each with dimensions x, x, and 1, added to three faces of the original cube.
- 3x: The volume of three rectangular prisms, each with dimensions x, 1, and 1, added to three edges of the original cube.
- 1: The volume of a small cube with dimensions 1 x 1 x 1 added to a corner.
By visualizing the addition of these volumes, we can understand how the expression represents the total volume of the larger cube with side length (x + 1). This geometric approach provides an intuitive understanding of the algebraic relationship.
Solving Equations: Finding the Roots
The expression x³ + 3x² + 3x + 1 = 0 is a cubic equation. Since we know its factorization, finding its roots (the values of x that make the equation true) is straightforward:
(x + 1)³ = 0
This implies:
x + 1 = 0
Therefore, the only real root of the equation is x = -1. This is a repeated root because (x + 1) is a factor three times. Understanding the roots is crucial for analyzing the behavior of the polynomial.
Applications: Beyond the Textbook
While this might seem like a purely theoretical exercise, understanding cubic polynomials like x³ + 3x² + 3x + 1 has practical applications in several fields:
-
Calculus: This expression serves as a fundamental example in calculus for differentiation and integration, crucial for understanding rates of change and areas under curves.
-
Physics and Engineering: Cubic equations appear in numerous physics and engineering problems, modeling phenomena such as projectile motion, fluid dynamics, and structural mechanics.
-
Computer Graphics and Animation: Cubic curves (related to cubic polynomials) are extensively used in computer graphics and animation to create smooth and realistic curves for modeling objects and simulating motion.
-
Data Analysis and Statistics: Cubic models are used in regression analysis to fit curves to data sets, allowing for the prediction of future values based on past trends.
Frequently Asked Questions (FAQ)
-
Q: What if the expression was x³ + 3x² + 3x + 2? A: This expression is not a perfect cube. It would require more advanced factoring techniques or numerical methods to solve the corresponding cubic equation.
-
Q: Can this expression be graphed? A: Yes. The graph of y = x³ + 3x² + 3x + 1 is a cubic curve. It will have a single x-intercept at x = -1 (since this is the only real root) and will generally increase as x increases.
-
Q: What is the significance of the coefficients (1, 3, 3, 1)? A: These coefficients are the binomial coefficients from the binomial expansion of (a + b)³ where a = x and b = 1. Their pattern is reflected in Pascal's Triangle, a key concept in combinatorics.
-
Q: Are there other perfect cube expressions? A: Absolutely! Any expression of the form (ax + b)³ will result in a perfect cube expression with coefficients determined by the binomial theorem.
Conclusion: A Journey into the Heart of Algebra
This exploration of the expression x³ + 3x² + 3x + 1 reveals that even seemingly simple mathematical expressions can hold profound mathematical significance. From its factorization and geometric interpretation to its application in various fields, this polynomial serves as a gateway to understanding deeper concepts in algebra and their real-world implications. By mastering the techniques discussed here, you'll gain a stronger foundation in mathematics and enhance your ability to tackle more complex problems. The journey of understanding is ongoing; keep exploring, keep questioning, and keep learning!
Latest Posts
Latest Posts
-
An Eap Is An Automotive
Sep 10, 2025
-
2 4 Mcg B12 To Mg
Sep 10, 2025
-
Convert 0 6 To A Fraction
Sep 10, 2025
-
7ft Is How Many Inches
Sep 10, 2025
-
How Much Is One Quart
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about X 3 3x 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.