Y 3 2y 7 76
cibeltiagestion
Sep 10, 2025 · 5 min read
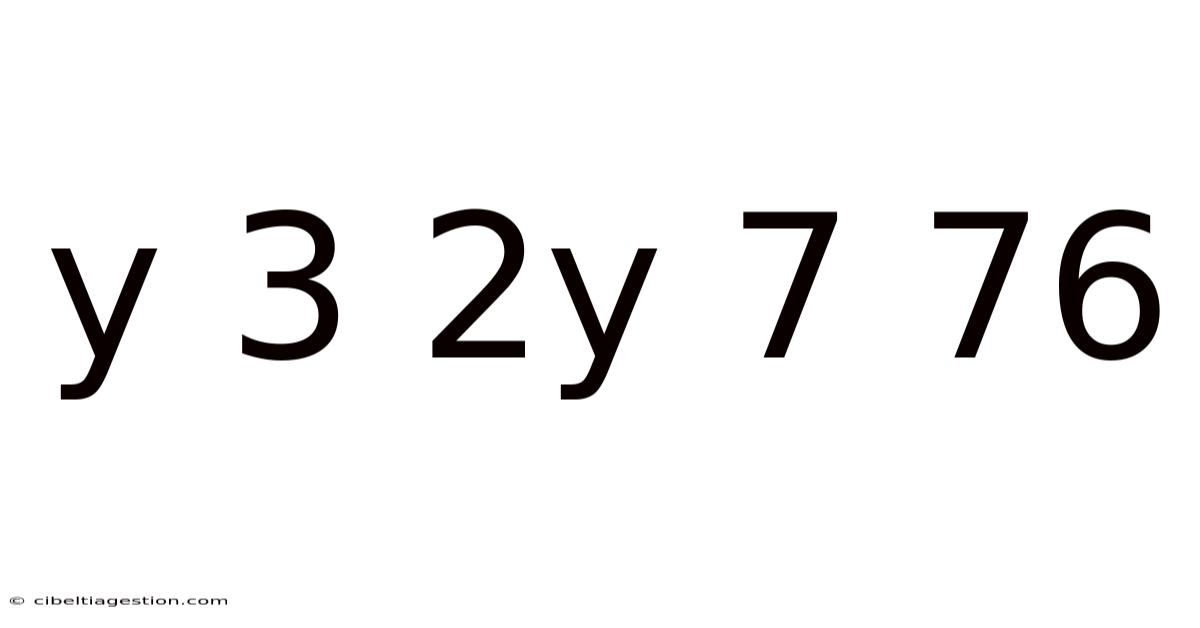
Table of Contents
Unraveling the Mystery: A Deep Dive into the Equation y³ + 2y² + 7y = 76
This article explores the cubic equation y³ + 2y² + 7y = 76, guiding you through its solution using various methods. We'll delve into the mathematical concepts involved, examine different approaches, and discuss the significance of such equations in various fields. Understanding cubic equations is crucial in numerous areas, from physics and engineering to economics and computer science. This comprehensive guide aims to provide a clear and accessible explanation, even for those with a limited mathematical background.
Introduction: Understanding Cubic Equations
A cubic equation is a polynomial equation of the third degree, meaning the highest power of the variable (in this case, y) is 3. The general form of a cubic equation is:
ax³ + bx² + cx + d = 0
where a, b, c, and d are constants, and a is not equal to zero. Our equation, y³ + 2y² + 7y = 76, can be rewritten in this standard form by subtracting 76 from both sides:
y³ + 2y² + 7y - 76 = 0
Solving cubic equations can be more complex than solving linear or quadratic equations. While there's a general formula (Cardano's formula), it can be quite cumbersome. Therefore, we'll explore several approaches to solving our specific equation, focusing on methods that are both effective and relatively straightforward.
Method 1: The Rational Root Theorem
The Rational Root Theorem helps us identify potential rational solutions (solutions that are fractions of integers). It states that if a polynomial equation with integer coefficients has a rational root p/q (where p and q are coprime integers), then p must be a factor of the constant term (in our case, -76) and q must be a factor of the leading coefficient (in our case, 1).
The factors of -76 are ±1, ±2, ±4, ±19, ±38, ±76. Since the leading coefficient is 1, the possible rational roots are simply these factors. We can test each one by substituting it into the equation:
- Testing y = 1: 1³ + 2(1)² + 7(1) - 76 = -66 ≠ 0
- Testing y = 2: 2³ + 2(2)² + 7(2) - 76 = 8 + 8 + 14 - 76 = -46 ≠ 0
- Testing y = 4: 4³ + 2(4)² + 7(4) - 76 = 64 + 32 + 28 - 76 = 48 ≠ 0
- Testing y = 19: 19³ + 2(19)² + 7(19) - 76 = 6859 + 722 + 133 - 76 = 7648 ≠ 0
- Testing y = -2: (-2)³ + 2(-2)² + 7(-2) - 76 = -8 + 8 - 14 - 76 = -90 ≠ 0
- Testing y = -4: (-4)³ + 2(-4)² + 7(-4) - 76 = -64 + 32 - 28 - 76 = -136 ≠ 0
- Testing y = -19: (-19)³ + 2(-19)² + 7(-19) - 76 = -6859 + 722 - 133 - 76 = -6346 ≠ 0
- Testing y = 38: 38³ + 2(38)² + 7(38) -76 = 54872 + 2888 + 266 - 76 = 57950 ≠ 0
- Testing y = -38: (-38)³ + 2(-38)² + 7(-38) - 76 = -54872 + 2888 - 266 - 76 = -52326 ≠ 0
- Testing y = 76: 76³ + 2(76)² + 7(76) - 76 = 438976 + 11552 + 532 -76 = 450984 ≠ 0
- Testing y = -76: (-76)³ + 2(-76)² + 7(-76) - 76 = -438976 + 11552 - 532 - 76 = -428032 ≠ 0
Unfortunately, none of the rational roots work. This indicates that the solutions are likely irrational or complex numbers.
Method 2: Numerical Methods
Since the Rational Root Theorem didn't yield a solution, we can employ numerical methods to approximate the real root(s). One common method is the Newton-Raphson method. This iterative method refines an initial guess to progressively closer approximations of the root. The formula is:
x_(n+1) = x_n - f(x_n) / f'(x_n)
where x_n is the current guess, x_(n+1) is the next guess, f(x_n) is the value of the function at x_n, and f'(x_n) is the derivative of the function at x_n.
For our equation, f(y) = y³ + 2y² + 7y - 76 and f'(y) = 3y² + 4y + 7. Applying the Newton-Raphson method requires an initial guess and iterative calculations. This is best done using a calculator or computer software.
Method 3: Graphing the Equation
Another approach is to graph the function f(y) = y³ + 2y² + 7y - 76. The x-intercept(s) of the graph represent the real root(s) of the equation. Using graphing software or a graphing calculator, we can visualize the function and estimate the root(s). The graph will show that there is one clear real root.
A Deeper Dive into Cubic Equation Solving
The general solution to a cubic equation involves a complex process, often referred to as Cardano's method. This method involves manipulating the equation to remove the quadratic term, then applying a substitution to transform it into a depressed cubic equation. The solution then involves cube roots and complex numbers, even if the final roots are real. Due to its complexity, we won't detail Cardano's method here, as numerical methods offer a more practical approach for this specific problem.
Applications of Cubic Equations
Cubic equations appear in various real-world applications:
- Engineering: Designing structures, analyzing fluid flow, and calculating the trajectory of projectiles.
- Physics: Modeling physical phenomena, such as the motion of objects under gravity or the behavior of electrical circuits.
- Economics: Modeling economic growth, analyzing market equilibrium, and optimizing resource allocation.
- Computer Science: Solving problems in computer graphics, algorithms, and data analysis.
Conclusion: Approximating the Solution
While we haven't found an exact analytical solution using simple methods for y³ + 2y² + 7y = 76, numerical methods like the Newton-Raphson method, or graphical analysis, provides a practical way to approximate the real root. The rational root theorem proved unsuccessful in finding rational roots. The existence of one clear real root, demonstrable through graphical means, highlights the importance of diverse mathematical approaches to problem-solving. Understanding cubic equations and the various techniques used to solve them is essential for anyone working in fields requiring quantitative analysis. Further exploration of numerical methods and specialized software would allow for a more precise determination of the solution. The journey of solving this cubic equation showcases the power and limitations of different mathematical tools and the importance of a multifaceted approach to tackling complex problems.
Latest Posts
Latest Posts
-
Magnesium 25 Protons Neutrons Electrons
Sep 10, 2025
-
37 9 Celsius To Fahrenheit
Sep 10, 2025
-
20 28 In Simplest Form
Sep 10, 2025
-
Noble Gas Configuration For Bismuth
Sep 10, 2025
-
1 3 Divided By 6
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Y 3 2y 7 76 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.