Y Mx B For X
cibeltiagestion
Sep 11, 2025 · 6 min read
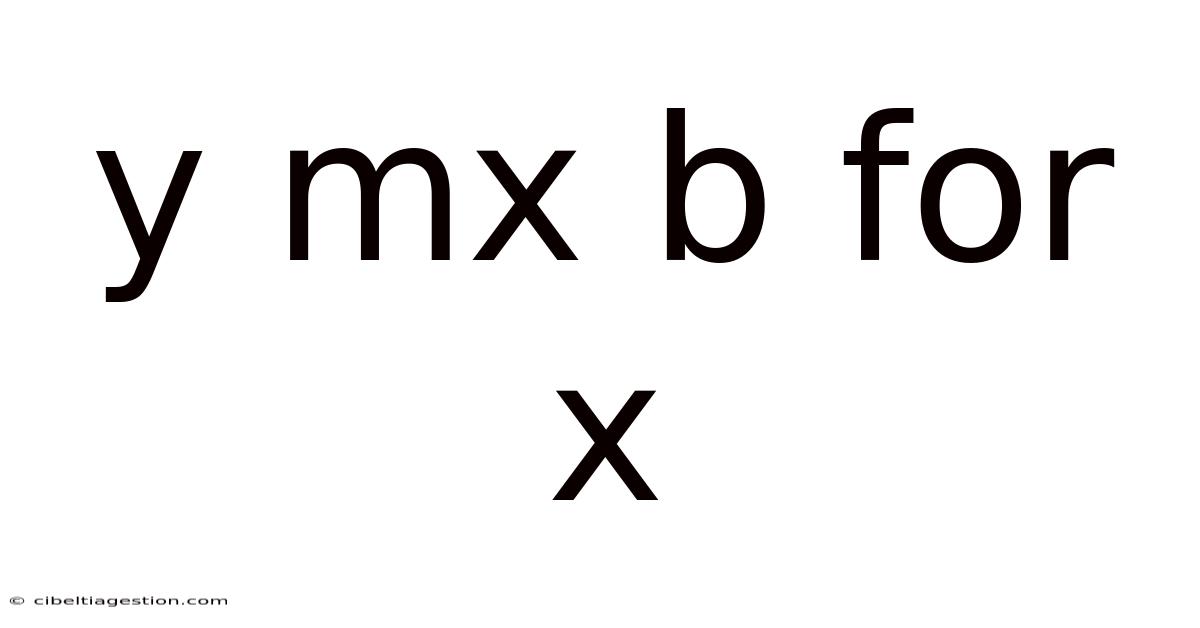
Table of Contents
Solving for x in y = mx + b: A Comprehensive Guide
The equation y = mx + b represents a fundamental concept in algebra and is the slope-intercept form of a linear equation. Understanding how to manipulate this equation, specifically solving for x, is crucial for various mathematical applications and problem-solving scenarios. This comprehensive guide will walk you through the process step-by-step, exploring different approaches and providing practical examples. We'll also delve into the underlying mathematical principles and address frequently asked questions. Whether you're a student struggling with algebra or simply looking to refresh your mathematical skills, this guide will equip you with the knowledge and confidence to master solving for x in y = mx + b.
Understanding the Equation: y = mx + b
Before we dive into solving for x, let's quickly review the components of the equation y = mx + b:
-
y: Represents the dependent variable, often plotted on the vertical axis of a graph. It's the value you're trying to find or predict.
-
m: Represents the slope of the line. The slope indicates the steepness and direction of the line. A positive slope indicates an upward trend, while a negative slope indicates a downward trend. The slope is calculated as the change in y divided by the change in x (rise over run).
-
x: Represents the independent variable, often plotted on the horizontal axis of a graph. This is the variable we are solving for. It’s the value that is being used to predict ‘y’.
-
b: Represents the y-intercept. This is the point where the line intersects the y-axis (where x = 0).
Steps to Solve for x in y = mx + b
Solving for x means isolating x on one side of the equation. Here's a step-by-step guide:
1. Subtract 'b' from both sides:
The first step is to eliminate the constant term (b) from the right-hand side of the equation. To do this, subtract b from both sides of the equation:
y - b = mx + b - b
This simplifies to:
y - b = mx
2. Divide both sides by 'm':
Now, we need to isolate x by removing the coefficient m. Since m is multiplied by x, we divide both sides of the equation by m:
(y - b) / m = mx / m
This simplifies to:
x = (y - b) / m
Important Note: This solution is valid only if m is not equal to zero. If m = 0, the equation becomes y = b, which represents a horizontal line, and there is no unique solution for x. In this case, x can be any real number.
Illustrative Examples
Let's solidify our understanding with some practical examples:
Example 1:
Solve for x in the equation y = 2x + 5, when y = 9.
-
Substitute y = 9 into the equation: 9 = 2x + 5
-
Subtract 5 from both sides: 9 - 5 = 2x => 4 = 2x
-
Divide both sides by 2: 4 / 2 = x => x = 2
Therefore, when y = 9, x = 2.
Example 2:
Solve for x in the equation y = -3x + 10, when y = 1.
-
Substitute y = 1 into the equation: 1 = -3x + 10
-
Subtract 10 from both sides: 1 - 10 = -3x => -9 = -3x
-
Divide both sides by -3: -9 / -3 = x => x = 3
Therefore, when y = 1, x = 3.
Example 3:
Solve for x in the equation y = (1/2)x - 4, when y = -2.
-
Substitute y = -2 into the equation: -2 = (1/2)x - 4
-
Add 4 to both sides: -2 + 4 = (1/2)x => 2 = (1/2)x
-
Multiply both sides by 2: 2 * 2 = x => x = 4
Therefore, when y = -2, x = 4.
Geometric Interpretation
The equation y = mx + b represents a straight line on a Cartesian coordinate system. Solving for x given a specific value of y corresponds geometrically to finding the x-coordinate of the point on the line where the y-coordinate is equal to the given value. This is essentially finding the intersection point of the line and a horizontal line at the specified y-value.
Applications of Solving for x
Solving for x in y = mx + b has numerous applications across various fields:
-
Physics: Many physical relationships can be modeled using linear equations. Solving for x allows you to determine a variable based on another known variable. For example, calculating distance based on speed and time.
-
Economics: Linear equations are used to model supply and demand, cost functions, and other economic relationships. Solving for x can help determine quantities based on prices or costs.
-
Engineering: Linear equations are used extensively in engineering calculations, especially in structural analysis and circuit design. Solving for x allows you to determine critical parameters in the system's design and function.
-
Computer Science: Linear equations are used in computer graphics, image processing, and machine learning algorithms. Solving for x is an important part of these computations.
Dealing with More Complex Scenarios
While the basic steps outlined above cover most scenarios, some equations might appear more complex initially. However, the core principle of isolating x remains the same. Let's consider a slightly more advanced example:
Example 4:
Solve for x in the equation 2y + 4 = 6x - 8, when y = 5.
-
Substitute y = 5 into the equation: 2(5) + 4 = 6x - 8
-
Simplify the left side: 10 + 4 = 6x - 8 => 14 = 6x - 8
-
Add 8 to both sides: 14 + 8 = 6x => 22 = 6x
-
Divide both sides by 6: 22 / 6 = x => x = 11/3 or approximately 3.67
Therefore, when y = 5, x = 11/3. This example demonstrates that even with a slightly more complex equation, the fundamental steps for solving for x remain the same. You just need to perform additional algebraic manipulations to isolate x.
Frequently Asked Questions (FAQ)
Q1: What happens if 'm' is 0?
If m = 0, the equation simplifies to y = b, which represents a horizontal line. In this case, x can take on any value, and there's no unique solution for x.
Q2: Can I solve for x if the equation is not in slope-intercept form?
Yes, you can. First, manipulate the equation algebraically to get it into the form y = mx + b, then follow the steps outlined above.
Q3: What if the equation involves fractions?
Follow the same steps, but be mindful of fraction arithmetic. Remember to find a common denominator when adding or subtracting fractions and to reciprocate and multiply when dividing by a fraction.
Conclusion
Solving for x in the equation y = mx + b is a fundamental algebraic skill with wide-ranging applications. By understanding the steps involved and practicing with different examples, you'll build a strong foundation in algebra and improve your problem-solving abilities. Remember the core principle: isolate x through systematic algebraic manipulation. This guide provides a thorough understanding of the process, making you confident in tackling various scenarios and applying this knowledge to real-world problems. Don’t hesitate to practice regularly to master this crucial concept. Remember to always check your work! Consistent practice and a clear understanding of the underlying principles will lead you to success.
Latest Posts
Latest Posts
-
Which System Has No Solution
Sep 11, 2025
-
Compound Formula For Calcium Phosphate
Sep 11, 2025
-
How Much Is 32 Ounces
Sep 11, 2025
-
Two Fifths Of A Number
Sep 11, 2025
-
How Much Is 2 Ounce
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Y Mx B For X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.