0.02 X 0.02 X 0.02
cibeltiagestion
Sep 13, 2025 · 6 min read
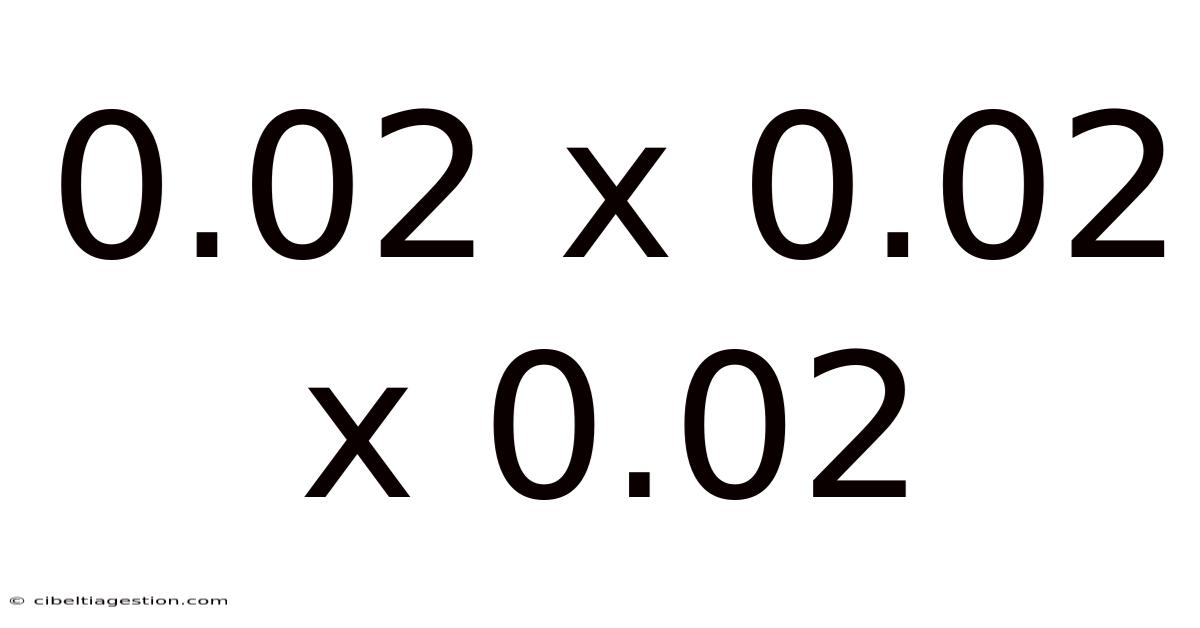
Table of Contents
Decoding the Tiny World: A Deep Dive into 0.02 x 0.02 x 0.02
This article explores the seemingly simple calculation of 0.02 x 0.02 x 0.02, delving beyond the immediate answer to uncover the underlying mathematical principles and real-world applications. We'll unpack the concept of cubic measurements, explore its relevance in various fields, and address common misconceptions. Understanding this seemingly insignificant calculation opens doors to comprehending more complex volumetric problems and the world of incredibly small scales.
Understanding the Basics: Multiplication and Cubic Units
At its core, 0.02 x 0.02 x 0.02 is a simple multiplication problem. We're multiplying three values, each representing 0.02 or two-hundredths. The result gives us the volume of a cube with sides measuring 0.02 units in length.
The units used are crucial. If our units are centimeters (cm), the answer represents a volume of 0.000008 cubic centimeters (cm³). If the units are meters (m), the volume would be 0.000008 cubic meters (m³). The "cubed" unit (cm³ or m³) signifies that we're dealing with a three-dimensional volume, not just a linear or square measurement. This distinction is essential in various scientific and engineering contexts.
The Calculation:
Performing the multiplication, we get:
0.02 x 0.02 = 0.0004
0.0004 x 0.02 = 0.000008
Therefore, 0.02 x 0.02 x 0.02 = 0.000008.
Visualizing the Cube: From Abstract Numbers to Concrete Reality
Imagine a tiny cube. Each side of this cube measures only 0.02 units long. This is incredibly small; for example, if the units are centimeters, each side is only 2 millimeters long. It's a cube you'd likely need a microscope to see clearly. The calculation 0.02 x 0.02 x 0.02 gives us the volume, or the amount of space this tiny cube occupies. Visualizing this small cube helps to put the abstract number 0.000008 into a more tangible context.
Real-World Applications: Where Tiny Cubes Matter
While seemingly insignificant, calculations involving small volumes like 0.000008 cubic units have significant applications in various fields:
-
Nanotechnology: Nanotechnology deals with materials at the atomic and molecular level. The volume of nanoparticles, which are often incredibly small, is crucial for understanding their behavior and properties. Calculations like 0.02 x 0.02 x 0.02, while possibly dealing with larger nanoparticles, illustrate the principles used in computing the volume of even smaller structures.
-
Microfluidics: Microfluidics involves manipulating tiny amounts of fluids in microscopic channels. Precise volume calculations are essential for controlling the flow and mixing of these fluids. The volume of small chambers or reaction areas within microfluidic devices can be represented by calculations similar to our example.
-
Material Science: In material science, researchers study the properties of materials at the microscopic and macroscopic level. Understanding the volume of tiny particles or pores within materials is crucial for determining their overall behavior and performance. This understanding is fundamental to designing new materials with specific properties.
-
Pharmacology and Drug Delivery: In drug development, precise volume measurements are crucial. The volume of drug particles, as well as the volume of drug delivery systems like nanoparticles, are essential factors in determining dosage and efficacy. Calculations like 0.02 x 0.02 x 0.02 can represent the simplified model of drug particle volume.
-
Medical Imaging: In medical imaging techniques like MRI and CT scans, extremely precise volumetric calculations are performed to reconstruct three-dimensional images of the body. These calculations are built upon fundamental concepts of volume measurement.
Scientific Notation and its Significance
The result, 0.000008, can be expressed more concisely using scientific notation: 8 x 10⁻⁶. Scientific notation is a standardized way of writing very large or very small numbers. It simplifies calculations and enhances readability, especially when dealing with numerous zeros. Understanding scientific notation is a cornerstone of scientific literacy.
Expanding the Concept: Beyond the Cube
The principle of calculating volume extends far beyond simple cubes. The formula for volume varies depending on the shape of the object. For example:
- Rectangular Prism (Cuboid): Volume = length x width x height.
- Sphere: Volume = (4/3)πr³, where 'r' is the radius.
- Cylinder: Volume = πr²h, where 'r' is the radius and 'h' is the height.
Understanding the underlying principles behind calculating the volume of a simple cube provides a foundational understanding that can be applied to calculate the volumes of more complex shapes.
Dealing with Units and Conversions
The accuracy of volume calculations heavily depends on the correct use and conversion of units. For instance, converting between cubic centimeters (cm³), cubic millimeters (mm³), and cubic meters (m³) requires careful attention to the conversion factors. One cubic centimeter is equal to 1000 cubic millimeters, and one cubic meter is equal to 1,000,000 cubic centimeters. These conversions are essential for maintaining consistency and accuracy in scientific calculations.
Common Misconceptions and How to Avoid Them
A common misconception is that multiplying decimals always results in a smaller number. While often true, it's not always the case. For instance, multiplying a decimal by a number greater than 1 would yield a larger result. Understanding the concept of place value and the impact of decimal points is crucial for performing accurate calculations.
Another misconception is overlooking the units. Always remember to include the appropriate units (cm³, m³, etc.) with your answer, as this conveys the physical meaning of the result. Ignoring units can lead to errors and misinterpretations.
Frequently Asked Questions (FAQs)
Q: What is the practical significance of calculating such a small volume?
A: Although 0.000008 cubic units seems insignificant, the principles involved in calculating this volume are fundamental to various scientific and engineering fields, particularly those dealing with nanoscale materials and microfluidic systems. The ability to calculate small volumes accurately is essential for numerous applications, from drug delivery to material science.
Q: Can this calculation be applied to other shapes besides cubes?
A: Yes, absolutely. The core concept of multiplying dimensions to find volume applies to various shapes, although the specific formulas differ depending on the shape (e.g., sphere, cylinder, cone). Understanding the volume of a cube is a crucial first step in understanding volumetric calculations for more complex shapes.
Q: How can I improve my skills in performing these types of calculations?
A: Practice is key. Work through numerous examples of volume calculations involving different shapes and units. Familiarize yourself with scientific notation to simplify calculations involving very large or very small numbers. Ensure a strong understanding of decimal multiplication and unit conversion.
Conclusion: The Power of Small Numbers
The seemingly trivial calculation of 0.02 x 0.02 x 0.02 reveals the power of fundamental mathematical principles. While the numerical result might appear insignificant, understanding the process and its applications in diverse fields underscores its profound importance. From the microscopic world of nanotechnology to the macroscopic scale of medical imaging, calculating volumes, even those as tiny as 0.000008 cubic units, remains a critical component of scientific and technological advancements. Mastering this fundamental concept opens the door to understanding more complex calculations and the intricate workings of our world at various scales.
Latest Posts
Latest Posts
-
What Is 75 Of 70
Sep 13, 2025
-
Convert 2 Pounds To Cups
Sep 13, 2025
-
B Type Climates Generally Occur
Sep 13, 2025
-
140 Percent As A Fraction
Sep 13, 2025
-
Y 2 X 1 2
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 0.02 X 0.02 X 0.02 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.