Y 2 X 1 2
cibeltiagestion
Sep 13, 2025 · 6 min read
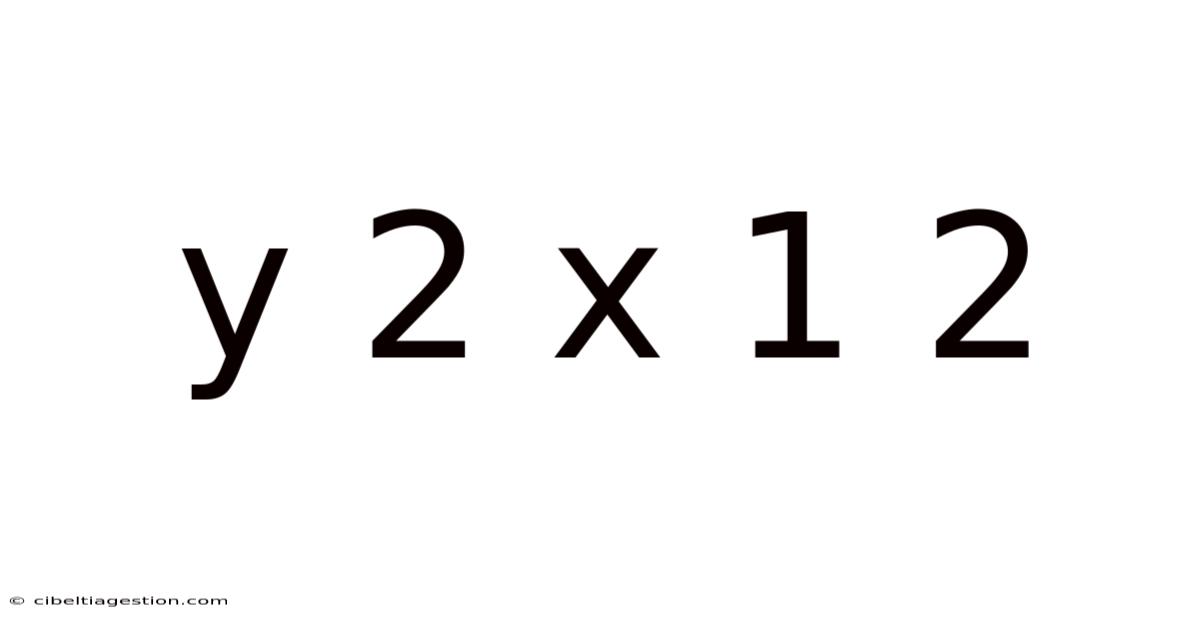
Table of Contents
Decoding the Enigma: A Deep Dive into "y = 2x + 12"
This article explores the linear equation y = 2x + 12, unpacking its meaning, applications, and underlying mathematical principles. We'll move beyond simple substitution and delve into graphing, slope-intercept form, real-world applications, and related concepts. Whether you're a student struggling with algebra or someone curious about the power of mathematical modeling, this comprehensive guide will illuminate the beauty and utility of this seemingly simple equation.
Understanding the Fundamentals: What Does y = 2x + 12 Represent?
At its core, y = 2x + 12 is a linear equation. This means it represents a straight line when graphed on a coordinate plane. The equation expresses a relationship between two variables, x and y, where y is dependent on x. Let's break down each component:
-
y: This is the dependent variable. Its value depends on the value of x. Think of y as the output or result.
-
x: This is the independent variable. You can choose any value for x, and the equation will tell you the corresponding value of y. x is the input.
-
2: This is the slope of the line. It represents the rate of change of y with respect to x. In this case, for every 1-unit increase in x, y increases by 2 units. The slope dictates the steepness and direction of the line.
-
12: This is the y-intercept. It's the point where the line crosses the y-axis (where x = 0). The y-intercept represents the initial value of y when x is zero.
Graphing the Equation: Visualizing the Relationship
Graphing y = 2x + 12 allows us to visualize the relationship between x and y. Here's how to do it:
-
Find the y-intercept: When x = 0, y = 12. This gives us the point (0, 12).
-
Use the slope to find another point: The slope is 2, which can be expressed as 2/1. This means that for every 1 unit increase in x, y increases by 2 units. Starting from (0, 12), move 1 unit to the right (increase x by 1) and 2 units up (increase y by 2). This gives us the point (1, 14).
-
Plot the points and draw the line: Plot the points (0, 12) and (1, 14) on a coordinate plane. Draw a straight line through these points. This line represents all the possible (x, y) pairs that satisfy the equation y = 2x + 12.
Slope-Intercept Form: Understanding the Structure
The equation y = 2x + 12 is written in slope-intercept form, which is generally expressed as:
y = mx + b
where:
- m is the slope
- b is the y-intercept
This form is incredibly useful because it allows you to quickly identify the slope and y-intercept of a linear equation. In our equation, m = 2 and b = 12.
Solving for x and y: Finding Specific Values
We can use the equation to find the value of y given a value of x, or vice versa.
Example 1: Finding y when x = 3
Substitute x = 3 into the equation:
y = 2(3) + 12 = 6 + 12 = 18
Therefore, when x = 3, y = 18.
Example 2: Finding x when y = 20
Substitute y = 20 into the equation:
20 = 2x + 12
Subtract 12 from both sides:
8 = 2x
Divide both sides by 2:
x = 4
Therefore, when y = 20, x = 4.
Real-World Applications: Where Does This Equation Show Up?
Linear equations like y = 2x + 12 are incredibly versatile and appear in numerous real-world scenarios. Here are a few examples:
-
Cost Calculation: Imagine a taxi service charges $12 as a base fare and $2 per kilometer. The total cost (y) can be modeled by the equation y = 2x + 12, where x is the number of kilometers traveled.
-
Profit Modeling: A company's profit (y) might be related to the number of units sold (x) by a linear equation. The 12 could represent fixed costs, and the 2 could represent profit per unit sold.
-
Temperature Conversion: While not a perfect linear relationship across all temperature scales, a simplified linear equation could approximate the conversion between Celsius and Fahrenheit over a specific range.
-
Physics and Engineering: Many physical phenomena, especially those involving constant rates of change, can be modeled using linear equations. Think of distance traveled at a constant speed, or the relationship between force and acceleration.
Beyond the Basics: Exploring Related Concepts
Understanding y = 2x + 12 opens doors to more advanced concepts:
-
Systems of Equations: Solving a system of linear equations involves finding the point where two or more lines intersect.
-
Linear Inequalities: Instead of an equals sign, you might encounter inequalities like y > 2x + 12 or y ≤ 2x + 12, which represent regions on the coordinate plane rather than just a line.
-
Matrices and Linear Transformations: Linear equations form the foundation for linear algebra, a powerful branch of mathematics used extensively in computer graphics, data analysis, and many other fields.
-
Calculus: The slope of a line is a fundamental concept that extends into the study of derivatives and rates of change in calculus.
Frequently Asked Questions (FAQ)
Q: What if the equation was y = -2x + 12? How would that change the graph?
A: The negative slope (-2) would indicate that the line slopes downwards from left to right, instead of upwards. The y-intercept would remain the same (12).
Q: Can this equation be written in other forms?
A: Yes, it can be rearranged to solve for x, resulting in x = (y-12)/2. It can also be expressed in standard form (Ax + By = C).
Q: How can I determine if a given point lies on the line represented by y = 2x + 12?
A: Substitute the x and y coordinates of the point into the equation. If the equation holds true, the point lies on the line.
Conclusion: The Significance of y = 2x + 12
While seemingly simple, the equation y = 2x + 12 serves as a foundational building block in mathematics and its applications. Understanding its components – the slope, the y-intercept, and the relationship between x and y – is crucial for grasping more complex mathematical concepts. From modeling real-world phenomena to solving systems of equations, this linear equation provides a gateway to a deeper appreciation of the power and elegance of mathematics. Its simplicity belies its profound impact across various disciplines, reinforcing the idea that even the most basic mathematical principles can unlock powerful insights and solutions. Continue exploring, asking questions, and pushing your understanding further – the world of mathematics is vast and rewarding!
Latest Posts
Latest Posts
-
Molar Mass Of Ammonium Phosphate
Sep 13, 2025
-
X 3 2x 2 3x
Sep 13, 2025
-
Aquellos Sombreros Son Muy Elegantes
Sep 13, 2025
-
X 2 Y 2 16
Sep 13, 2025
-
34x 25 How To Solve
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Y 2 X 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.