1/3 + 1/3 In Cups
cibeltiagestion
Sep 13, 2025 · 6 min read
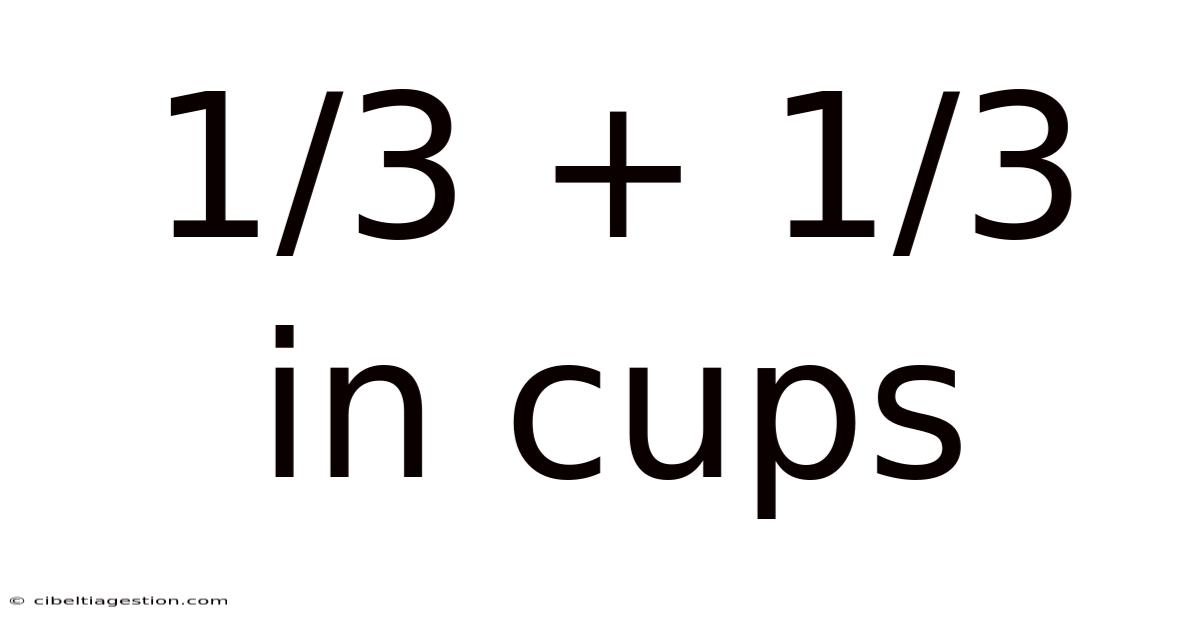
Table of Contents
1/3 + 1/3 in Cups: A Comprehensive Guide to Fraction Addition in Cooking
Adding fractions might seem daunting, especially when dealing with recipes and measurements in the kitchen. Understanding how to calculate 1/3 + 1/3 in cups is not just a math problem; it's a crucial skill for anyone who enjoys baking or cooking. This comprehensive guide will break down this seemingly simple calculation, exploring the underlying mathematical principles, providing practical applications, and addressing frequently asked questions. By the end, you’ll confidently tackle any fractional measurements in your culinary adventures.
Introduction: Why Understanding Fractions is Crucial in Cooking
Accuracy is key in cooking. A slight deviation in ingredient quantities can significantly impact the final outcome of a dish. Whether you're a seasoned chef or a baking novice, mastering the addition and subtraction of fractions, especially common ones like 1/3, is vital for consistent and successful results. This article specifically focuses on the addition of 1/3 + 1/3 cup, demonstrating the process and offering practical examples relevant to your kitchen. We'll delve into the mathematical explanation, highlighting why it works and offering various scenarios where this calculation is applicable.
Understanding the Basics: Adding Fractions with Common Denominators
Before we dive into the specific problem of 1/3 + 1/3, let's review the fundamental rules of adding fractions. The key principle lies in the denominator – the bottom number in a fraction. When adding fractions with the same denominator (like our 1/3 + 1/3 example), the process is straightforward:
-
Add the numerators: The numerators are the top numbers in the fractions. In our case, they are both 1. Adding them together gives us 1 + 1 = 2.
-
Keep the denominator the same: The denominator remains unchanged. Since both fractions have a denominator of 3, the denominator of our sum will also be 3.
-
Simplify the fraction (if possible): Our sum is now 2/3. This fraction cannot be simplified further because 2 and 3 have no common factors other than 1.
Calculating 1/3 + 1/3 in Cups: A Step-by-Step Guide
Applying the above rules to our specific problem, 1/3 cup + 1/3 cup, becomes a simple process:
-
Add the numerators: 1 + 1 = 2
-
Keep the denominator: The denominator remains 3.
-
Result: 1/3 cup + 1/3 cup = 2/3 cup
Visualizing the Calculation: A Practical Approach
Imagine you have two measuring cups. You fill one with 1/3 cup of flour and another with 1/3 cup of flour. If you pour both into a single, larger container, you'll have a total of 2/3 cup of flour. This visual representation reinforces the mathematical calculation, making it more intuitive and easy to understand.
Practical Applications in Cooking and Baking
Understanding 1/3 + 1/3 = 2/3 cup has countless applications in the kitchen:
-
Baking: Many recipes require precise measurements. If a recipe calls for 1/3 cup of sugar and 1/3 cup of butter, you'll need a total of 2/3 cup of the combined ingredients.
-
Cooking Sauces: When thickening sauces, you might need to add 1/3 cup of cornstarch slurry followed by another 1/3 cup to achieve the desired consistency. Understanding fraction addition ensures you add the correct amount.
-
Adjusting Recipes: If you want to halve a recipe that calls for 2/3 cup of an ingredient, you'll need to calculate half of 2/3, which involves understanding the initial addition of 1/3 + 1/3.
-
Portion Control: Understanding fractions is essential for dividing recipes into smaller portions or scaling them up or down for different numbers of servings.
-
Mixing Ingredients: Many cocktails and drinks use precise measurements, and knowing how to add fractions is useful for understanding the proportions of various ingredients.
Beyond 1/3 + 1/3: Adding Fractions with Different Denominators
While the example of 1/3 + 1/3 is straightforward, adding fractions with different denominators requires an additional step: finding a common denominator. This is the lowest common multiple (LCM) of the two denominators. For example, let's consider 1/3 + 1/2:
-
Find the Least Common Denominator (LCD): The LCD of 3 and 2 is 6.
-
Convert the fractions: To get a denominator of 6, we need to multiply the numerator and denominator of 1/3 by 2 (resulting in 2/6) and the numerator and denominator of 1/2 by 3 (resulting in 3/6).
-
Add the fractions: 2/6 + 3/6 = 5/6
Therefore, 1/3 + 1/2 = 5/6. This illustrates a slightly more complex scenario, but the underlying principle of adding numerators and maintaining a common denominator remains the same.
Addressing Common Misconceptions
A common mistake is to add both the numerators and denominators directly (e.g., incorrectly adding 1/3 + 1/3 as 2/6). Remember, you only add the numerators while keeping the common denominator unchanged. Understanding this fundamental principle is crucial to avoid errors in calculating fractional quantities.
Frequently Asked Questions (FAQ)
Q: What if I don't have a measuring cup that measures 1/3 cup?
A: You can use other measuring tools. Many measuring cups have markings for smaller fractions. Alternatively, you can use a liquid measuring cup and estimate the 1/3 cup mark. However, for baking, using a measuring cup that measures 1/3 cup precisely is recommended.
Q: Can I use a tablespoon or teaspoon to measure 1/3 cup?
A: Yes, there are conversion charts available that allow you to convert cup measurements to tablespoons and teaspoons. One cup equals 16 tablespoons and 48 teaspoons. So 1/3 cup equals approximately 5.33 tablespoons or 16 teaspoons. However, for accuracy, especially in baking, using a 1/3 cup measuring cup is the most reliable approach.
Q: How can I improve my understanding of fractions in cooking?
A: Practice is key. Try converting various fraction measurements to decimal equivalents or adding and subtracting different fraction amounts. Using visual aids like measuring cups can also help reinforce your understanding. You can find many practice problems and online resources to assist you.
Q: Are there any online tools or apps that can help with fractional calculations?
A: Yes, many online calculators and cooking apps offer fractional calculation tools. These tools can assist you with complex fraction operations, ensuring accurate ingredient measurements in your recipes.
Conclusion: Mastering Fraction Addition for Culinary Success
Mastering the simple addition of fractions, such as 1/3 + 1/3 = 2/3 cup, is a foundational skill for any aspiring or experienced cook or baker. This understanding ensures accuracy in following recipes, adjusting portion sizes, and ultimately achieving consistent and delicious results in your culinary creations. While initially seemingly simple, this skill extends far beyond a basic math problem and demonstrates practical application with significant impact on the quality and success of your cooking endeavors. Remember the key steps: add the numerators, keep the denominator consistent, and simplify your answer if necessary. Happy cooking!
Latest Posts
Latest Posts
-
65 Kilos How Many Pounds
Sep 13, 2025
-
Why Did America Enter Ww1
Sep 13, 2025
-
0 29 Acres In Sq Ft
Sep 13, 2025
-
2 1 2 Divided By 1 2
Sep 13, 2025
-
41 Degrees F To C
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 1/3 + 1/3 In Cups . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.