1/4 Is Greater Than 3/8
cibeltiagestion
Sep 14, 2025 · 6 min read
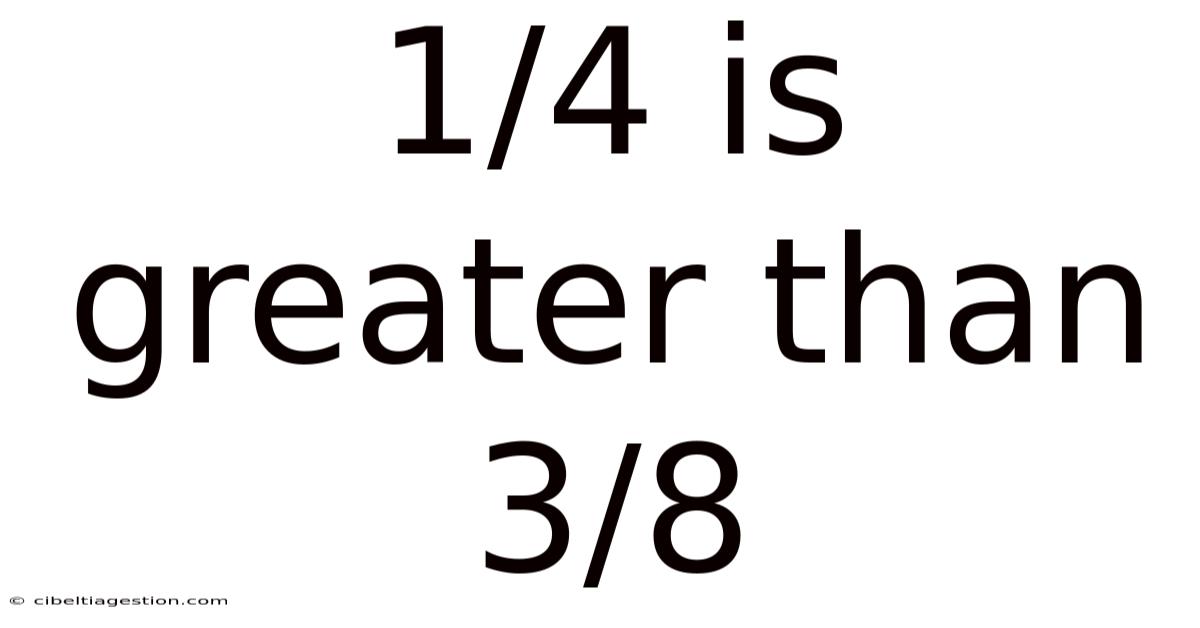
Table of Contents
Is 1/4 Greater Than 3/8? Unraveling Fraction Comparisons
Understanding fractions is fundamental to mathematics, and comparing them is a crucial skill. Many students struggle with this concept, often finding themselves perplexed when faced with seemingly simple comparisons like "Is 1/4 greater than 3/8?". This comprehensive guide will not only answer this question definitively but also equip you with the tools and understanding to confidently compare any two fractions. We'll explore multiple methods, delve into the underlying mathematical principles, and address common misconceptions. By the end, you’ll be able to tackle fraction comparisons with ease and confidence.
Introduction: Understanding Fractions
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), separated by a horizontal line. The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/4, the numerator (1) tells us we have one part, and the denominator (4) tells us the whole is divided into four equal parts.
Method 1: Finding a Common Denominator
The most common and reliable method for comparing fractions is to find a common denominator. This means finding a number that is a multiple of both denominators. Once both fractions have the same denominator, we can simply compare the numerators.
Let's apply this to our question: Is 1/4 greater than 3/8?
-
Step 1: Find a common denominator for 4 and 8. The smallest common multiple of 4 and 8 is 8.
-
Step 2: Convert 1/4 to an equivalent fraction with a denominator of 8. To do this, we ask ourselves: "What number multiplied by 4 gives us 8?". The answer is 2. We then multiply both the numerator and the denominator of 1/4 by 2:
(1 x 2) / (4 x 2) = 2/8
-
Step 3: Compare the numerators. Now we have 2/8 and 3/8. Since both fractions have the same denominator, we can directly compare their numerators: 2 is less than 3.
-
Conclusion: Therefore, 1/4 (which is equal to 2/8) is not greater than 3/8. In fact, 1/4 is less than 3/8.
Method 2: Visual Representation
Visual aids can be incredibly helpful in understanding fraction comparisons. Let's use a visual representation to illustrate the comparison between 1/4 and 3/8.
Imagine two identical squares.
-
Representing 1/4: Divide the first square into four equal parts. Shade one of those parts. This visually represents 1/4.
-
Representing 3/8: Divide the second square into eight equal parts. Shade three of those parts. This visually represents 3/8.
By comparing the shaded areas, you can clearly see that the shaded area representing 3/8 is larger than the shaded area representing 1/4. This confirms that 1/4 is less than 3/8.
Method 3: Converting to Decimals
Another effective method involves converting fractions to decimals. This is particularly useful when comparing fractions with different denominators that are not easily converted to a common denominator.
-
Converting 1/4 to a decimal: Divide the numerator (1) by the denominator (4): 1 ÷ 4 = 0.25
-
Converting 3/8 to a decimal: Divide the numerator (3) by the denominator (8): 3 ÷ 8 = 0.375
Comparing the decimal values, 0.25 is less than 0.375. This confirms that 1/4 is less than 3/8.
The Mathematical Explanation: Why this is True
The reason 1/4 is less than 3/8 stems from the fundamental concept of fractions representing parts of a whole. When we express both fractions with a common denominator (as we did in Method 1), we are essentially comparing equal-sized pieces of the same whole. Since 2/8 (equivalent to 1/4) has fewer parts shaded than 3/8, it represents a smaller portion of the whole.
Addressing Common Misconceptions
A frequent mistake students make is comparing numerators and denominators independently. For instance, some might incorrectly conclude that 1/4 is greater than 3/8 because 4 (the denominator of 1/4) is larger than 3 (the numerator of 3/8). This is incorrect; the denominator and numerator must be considered together as a single entity representing a part of a whole.
Beyond the Basics: Extending the Comparison Skills
The methods outlined above are not just limited to comparing 1/4 and 3/8. They can be applied to any fraction comparison. Mastering these techniques will provide a solid foundation for more complex mathematical concepts involving fractions, such as adding, subtracting, multiplying, and dividing fractions, as well as working with mixed numbers and improper fractions.
Frequently Asked Questions (FAQ)
Q1: Are there other ways to compare fractions besides the ones mentioned?
A1: Yes, there are other approaches, such as using cross-multiplication. However, the methods described (common denominator, visual representation, and decimal conversion) are generally the most intuitive and easiest to grasp for beginners.
Q2: What if the fractions have very large denominators?
A2: Finding the least common multiple of large numbers might be challenging. In such cases, converting to decimals is often the more efficient approach.
Q3: Is there a quick way to estimate which fraction is larger without performing calculations?
A3: Sometimes, a quick mental estimation is possible. If one fraction is clearly more than half (i.e., its numerator is more than half its denominator) and the other is less than half, you can quickly determine which is larger. However, this approach is not always reliable and shouldn't replace the accurate methods described above.
Q4: Why is understanding fraction comparison important?
A4: Fraction comparison is a fundamental skill crucial for various applications in mathematics and everyday life. It forms the basis for further study of fractions, decimals, percentages, ratios, and proportions. It also plays a vital role in solving real-world problems involving measurements, cooking, and many other areas.
Conclusion: Mastering Fraction Comparison
Comparing fractions, while seemingly simple, requires a firm grasp of fundamental concepts. By understanding the methods of finding a common denominator, using visual aids, and converting to decimals, you can confidently compare any two fractions. Remember to avoid common misconceptions and always consider the relationship between the numerator and the denominator. With practice, you will develop the skills to tackle fraction comparisons with ease and accuracy, laying a strong foundation for more advanced mathematical concepts. The key is to choose the method that works best for you and to consistently practice until you feel comfortable with the process. The ability to confidently compare fractions will significantly enhance your mathematical abilities and open doors to a deeper understanding of the world around you.
Latest Posts
Latest Posts
-
Scientific Name For A Sheep
Sep 14, 2025
-
Which Term Describes An Enzyme
Sep 14, 2025
-
Formula For Mercury Ii Oxide
Sep 14, 2025
-
48 Degrees Farenheit To Celcius
Sep 14, 2025
-
11 10 As A Mixed Number
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 1/4 Is Greater Than 3/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.