1 8 Divided 3 4
cibeltiagestion
Sep 10, 2025 · 5 min read
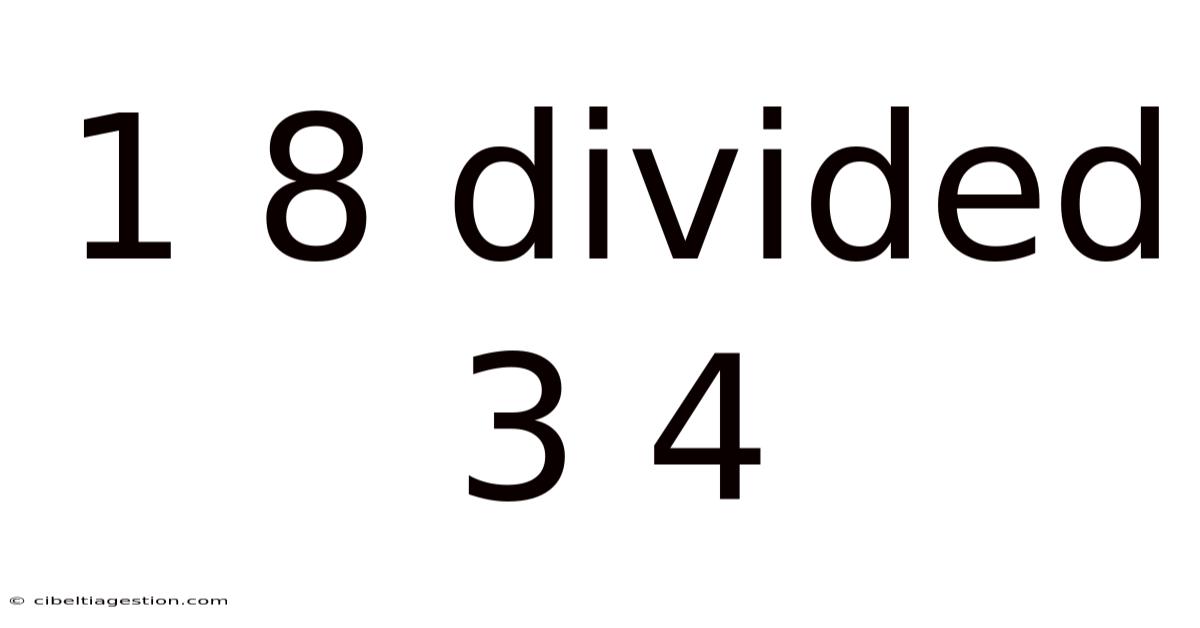
Table of Contents
Decoding 1 8 Divided by 3 4: A Comprehensive Guide to Mixed Number Division
This article explores the seemingly simple yet often confusing calculation: 1 8 divided by 3 4. We'll break down the process step-by-step, providing a clear understanding of the underlying mathematical principles and addressing common misconceptions. Understanding this type of division is crucial for mastering arithmetic and tackling more complex mathematical problems later on. We'll delve into the intricacies of dividing mixed numbers, highlighting efficient techniques and offering helpful strategies for solving similar problems. This guide will serve as a valuable resource for students, teachers, and anyone looking to improve their mathematical skills.
Understanding Mixed Numbers
Before we tackle the division problem, let's review mixed numbers. A mixed number combines a whole number and a fraction. For example, 1 8 represents one whole unit and eight-tenths of another unit. To perform calculations involving mixed numbers, we often need to convert them into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
To convert a mixed number to an improper fraction, we follow these steps:
- Multiply the whole number by the denominator of the fraction. In our example, 1 × 10 = 10.
- Add the result to the numerator of the fraction. 10 + 8 = 18.
- Keep the same denominator. The denominator remains 10.
Therefore, 1 8 converted to an improper fraction is 18/10. Similarly, 3 4 converts to:
- 3 × 10 = 30
- 30 + 4 = 34
- Denominator remains 10
So, 3 4 becomes 34/10.
Now our problem becomes: 18/10 ÷ 34/10
Dividing Fractions: The Reciprocal Method
Dividing fractions involves a crucial concept: the reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2, and the reciprocal of 5/7 is 7/5.
To divide fractions, we follow these steps:
- Convert any mixed numbers to improper fractions (as we've already done).
- Change the division sign to a multiplication sign.
- Replace the second fraction (the divisor) with its reciprocal.
- Multiply the numerators together.
- Multiply the denominators together.
- Simplify the resulting fraction if possible.
Let's apply these steps to our problem:
18/10 ÷ 34/10 becomes 18/10 × 10/34
Now we multiply:
(18 × 10) / (10 × 34) = 180/340
This fraction can be simplified. Both the numerator and denominator are divisible by 10:
180/340 = 18/34
We can further simplify by dividing both by 2:
18/34 = 9/17
Therefore, 1 8 divided by 3 4 is equal to 9/17.
Alternative Approach: Decimal Conversion
Another method to solve this problem is to convert the mixed numbers into decimals before performing the division.
1 8 is equal to 1.8, and 3 4 is equal to 3.4.
Therefore, the problem becomes 1.8 ÷ 3.4. Using a calculator or long division:
1.8 ÷ 3.4 ≈ 0.5294
To convert this decimal back to a fraction, we can use a process of approximation. While not perfectly precise without a calculator, we observe that 0.5294 is approximately 0.53, which is close to 53/100. However, this approach is not as straightforward as the fraction method.
The fraction method delivers a precise answer without the need for approximation.
Understanding the Result: 9/17
The result, 9/17, is an improper fraction (meaning the numerator is smaller than the denominator), representing a value less than 1. This makes sense intuitively, as we're dividing a smaller mixed number (1 8) by a larger mixed number (3 4). Converting 9/17 to a decimal using a calculator yields approximately 0.529, which is consistent with the decimal approach, confirming our result.
Frequently Asked Questions (FAQs)
-
Why is converting to improper fractions necessary? It's essential because it allows us to apply the standard rules of fraction division directly. Trying to divide mixed numbers directly can lead to errors and confusion.
-
Can I use a calculator? While calculators are helpful for checking your work, understanding the underlying mathematical principles is crucial for developing your mathematical skills. Mastering the manual method helps in comprehending the concept, and you'll be able to apply it in more complex scenarios where a calculator might not be readily available.
-
What if the denominators are different? The process remains the same. Convert any mixed numbers to improper fractions, find the reciprocal of the divisor, and then multiply. The only additional step is that you may need to find a common denominator before performing multiplication if the denominators are different; however, this step was not required in this instance, because the denominators were already the same.
-
How can I simplify fractions effectively? Look for common factors in the numerator and denominator. Divide both by their greatest common divisor (GCD) to obtain the simplest form of the fraction. For example, finding the GCD of 180 and 340 is 10, leading to the simplification to 18/34. Further simplification using GCD 2 gives us 9/17.
-
What if I get a decimal answer? Decimal answers are acceptable. Round to a reasonable number of decimal places depending on the context and the precision required.
Conclusion
Dividing mixed numbers like 1 8 by 3 4 may seem daunting at first, but by systematically converting to improper fractions and applying the rules of fraction division, the process becomes straightforward. Remember to always convert mixed numbers to improper fractions before beginning the division process. Mastering this fundamental skill will lay a strong foundation for more advanced mathematical concepts. The steps involved, from converting mixed numbers to finding the reciprocal and simplifying the fraction, will equip you with essential problem-solving tools applicable in various mathematical contexts. By understanding both the fraction and decimal approaches, you'll develop a more complete understanding of this essential arithmetic operation. Keep practicing, and you’ll become proficient in dividing mixed numbers with confidence!
Latest Posts
Latest Posts
-
Dietary Recalls Include Information About
Sep 10, 2025
-
Before Heavily Soiled Condiment Pans
Sep 10, 2025
-
What Is 2 Of 180
Sep 10, 2025
-
What Is 25 Of 520
Sep 10, 2025
-
Assuming You Tested An Organism
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 1 8 Divided 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.