1 9 X 2 0
cibeltiagestion
Sep 15, 2025 · 5 min read
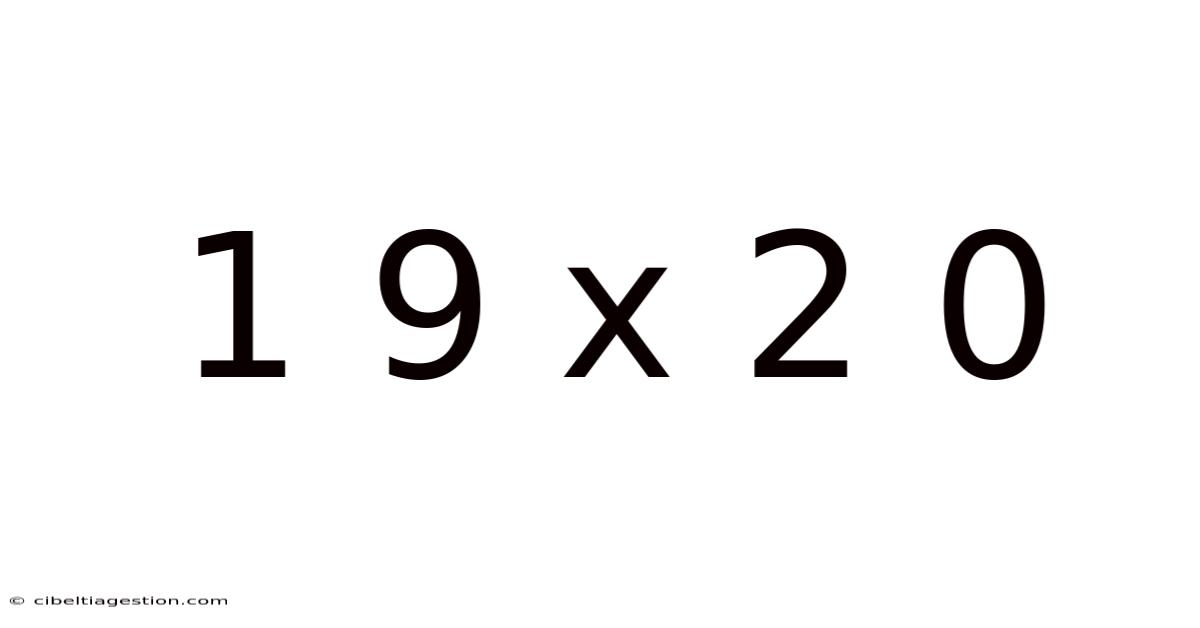
Table of Contents
Decoding 19 x 20: A Deep Dive into Multiplication and Beyond
The seemingly simple calculation of 19 x 20 might seem trivial at first glance. However, this seemingly basic arithmetic problem opens doors to explore fundamental concepts in mathematics, including multiplication, distributive property, mental math techniques, and even touches upon more advanced ideas like number theory. This article will delve into various approaches to solving 19 x 20, demonstrating diverse problem-solving skills and highlighting the interconnectedness of mathematical concepts. Understanding this seemingly simple problem provides a strong foundation for more complex mathematical endeavors.
Understanding the Fundamentals: Multiplication
At its core, 19 x 20 represents repeated addition. It signifies adding the number 19 to itself 20 times. While this method is feasible, it's time-consuming and impractical for larger numbers. Multiplication offers a more efficient method to solve this. Understanding the concept of multiplication as repeated addition is crucial for grasping its application in various contexts. Multiplication is essentially a shortcut to repeated addition.
Methods for Solving 19 x 20
Several methods exist to solve 19 x 20 efficiently, catering to different skill levels and mathematical preferences:
1. Standard Multiplication Algorithm:
This is the traditional method taught in schools. It involves multiplying each digit of the first number (19) by each digit of the second number (20) and then adding the partial products.
- Step 1: Multiply 9 (units digit of 19) by 0 (units digit of 20): 9 x 0 = 0
- Step 2: Multiply 9 by 2 (tens digit of 20): 9 x 2 = 18 (write 8 and carry-over 1)
- Step 3: Multiply 1 (tens digit of 19) by 0: 1 x 0 = 0
- Step 4: Multiply 1 by 2: 1 x 2 = 2
- Step 5: Add the partial products: 0 + 180 + 0 + 200 = 380
Therefore, 19 x 20 = 380
2. Distributive Property:
The distributive property states that a(b + c) = ab + ac. We can utilize this property to simplify the calculation:
- Rewrite 19 as (20 - 1).
- Then, 19 x 20 becomes (20 - 1) x 20.
- Applying the distributive property: (20 x 20) - (1 x 20) = 400 - 20 = 380.
This method showcases a powerful algebraic concept and simplifies the calculation by using easier multiplications.
3. Mental Math Techniques:
For those comfortable with mental calculations, several shortcuts exist:
- Rounding and Adjustment: Round 19 up to 20. Then, calculate 20 x 20 = 400. Since we added 1 to 19, we subtract the extra 20 (1 x 20): 400 - 20 = 380.
- Factoring: Recognize that 20 is a multiple of 10. Therefore, we can multiply 19 by 2 and then add a zero: 19 x 2 = 38. Adding a zero gives 380.
These methods highlight the versatility of mathematical thinking and emphasize the importance of recognizing patterns and relationships between numbers.
Exploring Related Concepts: Number Theory and Factors
The problem 19 x 20 touches upon several concepts within number theory. Analyzing the factors of 19 and 20 reveals valuable insights:
- Prime Factorization: 19 is a prime number (only divisible by 1 and itself). 20 can be factorized as 2 x 2 x 5 (2² x 5). Understanding prime factorization is a fundamental concept in number theory and cryptography.
- Common Factors: 19 and 20 share no common factors other than 1, indicating they are relatively prime. This concept is important in various mathematical contexts, including simplifying fractions.
- Multiples: 380 is a multiple of both 19 and 20. Understanding multiples helps in solving various arithmetic and algebraic problems.
Practical Applications: Real-World Scenarios
The ability to quickly and accurately solve problems like 19 x 20 has practical applications in various real-world scenarios:
- Shopping: Calculating the total cost of 19 items priced at $20 each.
- Construction: Determining the total length of 20 pieces of wood, each measuring 19 inches.
- Finance: Calculating simple interest or total earnings based on a specific rate and duration.
- Data Analysis: Simple calculations are often building blocks for more complex data analysis tasks.
Understanding and mastering basic arithmetic operations like multiplication is fundamental to problem-solving in various professional and personal contexts.
Frequently Asked Questions (FAQs)
Q: What is the easiest way to calculate 19 x 20?
A: The easiest way depends on individual preferences and mathematical strengths. The distributive property ((20-1) x 20) or the mental math technique of rounding and adjusting (20 x 20 - 20) are generally considered efficient methods.
Q: Is there a faster way than the standard multiplication algorithm?
A: Yes, the distributive property and mental math techniques often offer faster calculations, especially for numbers close to easy multiples of 10 or 100.
Q: Why is understanding prime factorization important?
A: Prime factorization is fundamental in number theory, simplifying fractions, and finding greatest common divisors (GCD) and least common multiples (LCM), all essential in various mathematical applications.
Q: Can this calculation be solved using a calculator?
A: Absolutely. Calculators are useful tools for verifying answers and handling larger or more complex calculations. However, understanding the underlying mathematical concepts is vital for developing problem-solving skills and mathematical intuition.
Conclusion: Beyond the Numbers
The seemingly simple problem of 19 x 20 provides a gateway to explore a vast range of mathematical concepts. From the fundamental principles of multiplication and the distributive property to more advanced ideas within number theory, this calculation showcases the interconnectedness and practical applications of mathematics. By understanding different methods of solving this problem, we cultivate valuable problem-solving skills, improve mathematical fluency, and appreciate the beauty and elegance of mathematical relationships. The key takeaway is not just the answer (380), but the journey of exploration and the understanding gained along the way. This seemingly simple problem serves as a powerful reminder of the depth and breadth hidden within even the most basic mathematical operations. Mastering such fundamentals lays a strong foundation for tackling more challenging mathematical problems in the future, building confidence and a deep appreciation for the power of numbers.
Latest Posts
Latest Posts
-
Mg3 Po4 2 Compound Name
Sep 15, 2025
-
X 2 5x 2 0
Sep 15, 2025
-
What Is A Collective Farm
Sep 15, 2025
-
How Do You Spell Yawn
Sep 15, 2025
-
How Long Is 90 Mins
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 1 9 X 2 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.