X 2 5x 2 0
cibeltiagestion
Sep 15, 2025 · 5 min read
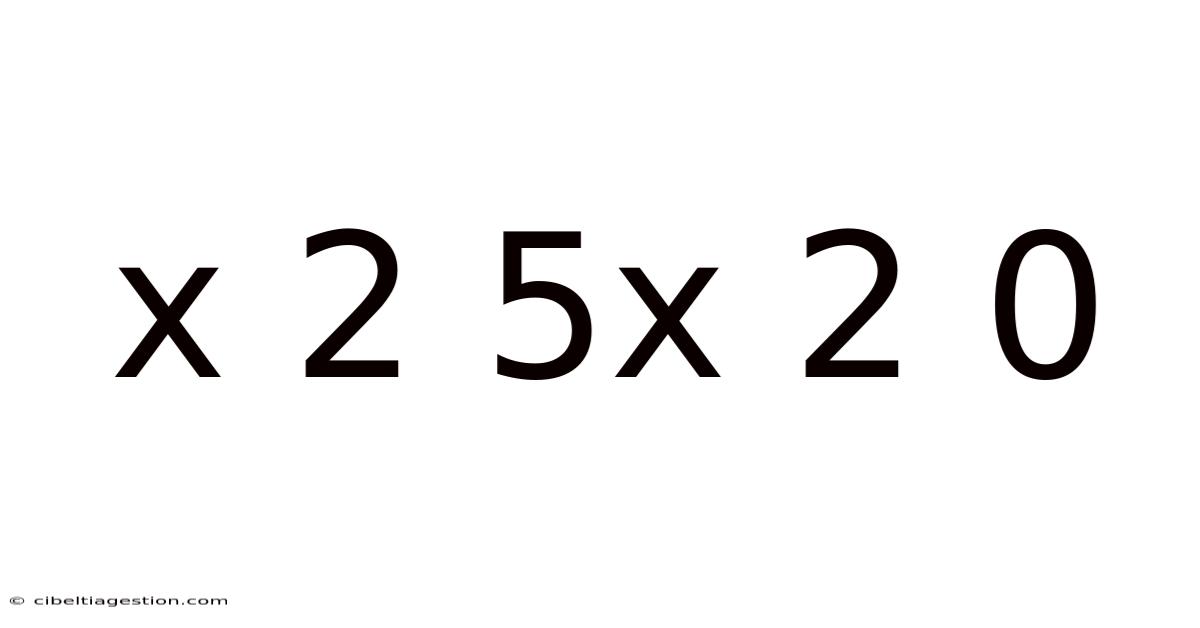
Table of Contents
Decoding the Mystery: x² + 5x² + 0
This article delves into the seemingly simple algebraic expression x² + 5x² + 0, exploring its simplification, the underlying mathematical concepts, and its applications in various fields. Understanding this expression provides a foundational understanding of polynomial algebra, a crucial element in many areas of mathematics and science. We will break down the process step-by-step, ensuring that even those with limited mathematical backgrounds can grasp the concepts easily.
Understanding the Components
Before we begin simplifying, let's examine each part of the expression: x² + 5x² + 0.
-
x² (x squared): This represents x multiplied by itself (x * x). It's a quadratic term, meaning it has a degree of 2 (the highest power of the variable). The 'x' is a variable, representing an unknown value.
-
5x²: This is also a quadratic term. The '5' is the coefficient, a number that multiplies the variable term. It indicates we have five instances of x².
-
0: This is a constant term. Constants are numerical values that don't involve variables. In this case, it's simply zero.
Simplifying the Expression
Simplifying the expression x² + 5x² + 0 involves combining like terms. Like terms are terms that have the same variable raised to the same power. In our expression, both x² and 5x² are like terms.
To simplify, we add the coefficients of the like terms:
1x² + 5x² = (1 + 5)x² = 6x²
The constant term, 0, doesn't affect the simplification since adding zero to any value doesn't change its value.
Therefore, the simplified form of x² + 5x² + 0 is 6x².
The Principles of Polynomial Algebra
This simplification exemplifies fundamental principles of polynomial algebra:
-
Combining Like Terms: The core principle is combining terms with the same variable and exponent. This is based on the distributive property of multiplication over addition: a(b + c) = ab + ac. In our case, we can factor out x²: x²(1 + 5) = 6x².
-
Polynomials: The expression x² + 5x² + 0 is a polynomial. Specifically, it's a monomial (a polynomial with one term) once simplified to 6x². Polynomials are algebraic expressions consisting of variables and constants, combined using addition, subtraction, and multiplication. They are classified by their degree (the highest power of the variable). Our simplified expression has a degree of 2, making it a quadratic monomial.
-
Coefficients and Variables: Understanding coefficients and variables is essential. The coefficient represents the quantity of the variable term, while the variable represents an unknown value or a quantity that can vary.
Applications of Quadratic Expressions
Quadratic expressions, like our simplified 6x², appear extensively in various fields:
-
Physics: They describe projectile motion, the path of objects under gravity. The height of a projectile at a given time can be represented by a quadratic equation.
-
Engineering: Quadratic equations are crucial in structural analysis, determining the forces and stresses on structures like bridges and buildings.
-
Economics: Quadratic functions can model cost functions, revenue functions, and profit functions in business applications.
-
Computer Graphics: Quadratic curves (parabolas) are used in creating curved shapes and animations in computer graphics and game development.
-
Data Analysis: Quadratic regression analysis helps to fit quadratic models to data sets, allowing for better prediction and understanding of trends.
Expanding the Concept: More Complex Scenarios
Let's consider more complex scenarios involving similar principles:
Example 1: 3x² + 2x + 4x² - x
Here, we have multiple like terms. We can combine the x² terms and the x terms separately:
(3x² + 4x²) + (2x - x) = 7x² + x
Example 2: 2x³ + 5x² - x³ + 3x²
In this example, we have different powers of x. We combine like terms based on the exponent:
(2x³ - x³) + (5x² + 3x²) = x³ + 8x²
Example 3: (x + 2)(x + 3)
This is a binomial expansion. We use the FOIL method (First, Outer, Inner, Last):
(x + 2)(x + 3) = x² + 3x + 2x + 6 = x² + 5x + 6
This example demonstrates that expanding expressions can sometimes result in combining like terms afterward.
Frequently Asked Questions (FAQs)
Q1: What is the difference between a term, a coefficient, and a variable?
- Term: A term is a single number, variable, or the product of numbers and variables. Examples: 5x², 3x, 7.
- Coefficient: The numerical factor in a term. In 5x², 5 is the coefficient.
- Variable: A symbol (usually a letter) representing an unknown value or a quantity that can change. In 5x², x is the variable.
Q2: Why is it important to simplify algebraic expressions?
Simplifying expressions makes them easier to understand, work with, and solve. Simplified expressions are more manageable in problem-solving and lead to more efficient calculations.
Q3: Can I simplify expressions with different variables?
You can only combine like terms. If the terms have different variables or different exponents, they cannot be combined. For example, 2x² and 3y cannot be simplified further.
Q4: What happens if I have a negative coefficient?
Negative coefficients are handled the same way as positive coefficients. Simply add or subtract them accordingly. For example: 5x² - 2x² = 3x²
Q5: What are some common mistakes to avoid when simplifying expressions?
- Adding unlike terms: Remember, you can only combine like terms.
- Incorrectly applying the order of operations: Follow PEMDAS/BODMAS (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction).
- Forgetting to distribute correctly: When expanding expressions, distribute the terms accurately.
Conclusion
The seemingly simple expression x² + 5x² + 0, when simplified to 6x², provides a powerful entry point into the world of polynomial algebra. Understanding its simplification involves grasping the fundamentals of like terms, coefficients, and variables. These concepts are broadly applicable across various disciplines, from physics and engineering to economics and computer science. By mastering these basic principles, you pave the way for tackling more complex algebraic expressions and equations, further developing your mathematical skills and problem-solving abilities. The journey from a simple expression to a deeper understanding of polynomial algebra is a rewarding one, opening up a wide range of opportunities for further exploration and application.
Latest Posts
Latest Posts
-
1963 Twenty Dollar Bill Worth
Sep 15, 2025
-
What Is 70 Of 50
Sep 15, 2025
-
How Many Weeks Is Summer
Sep 15, 2025
-
Equipotentials Are Lines Along Which
Sep 15, 2025
-
Can Theocracy Coexist With Democracy
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X 2 5x 2 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.