15 Of What Is 30
cibeltiagestion
Sep 07, 2025 · 5 min read
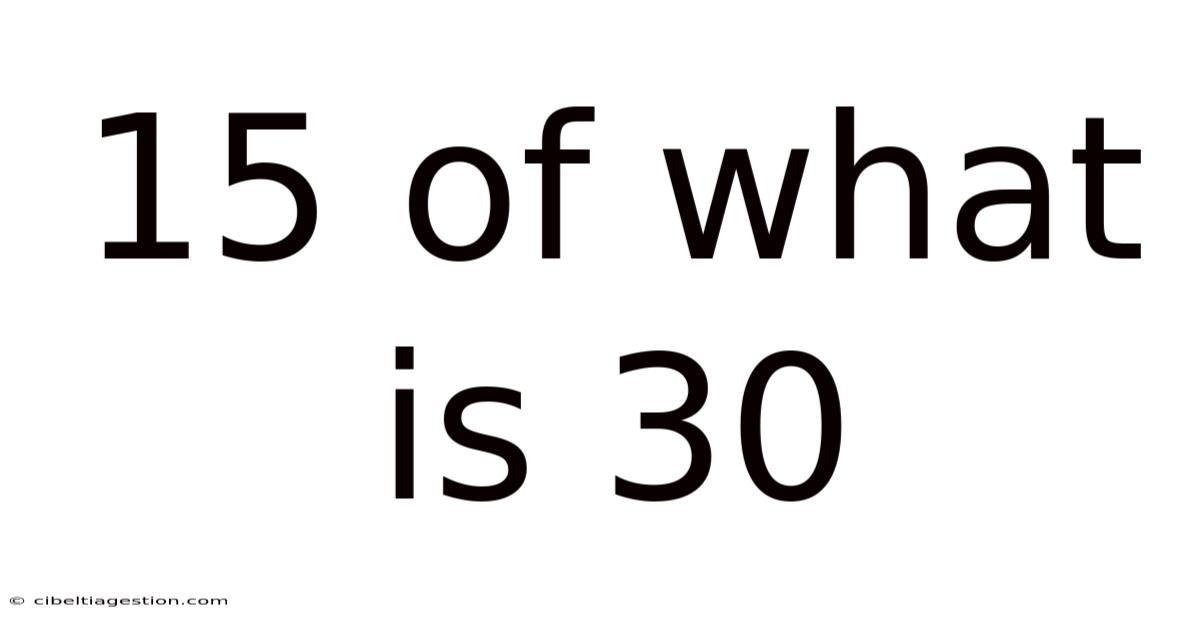
Table of Contents
Unveiling the Mystery: 15 of What is 30? A Deep Dive into Fractions, Ratios, and Proportions
Understanding fractions, ratios, and proportions is fundamental to numerous aspects of life, from baking a cake to calculating financial investments. This comprehensive guide delves into the seemingly simple question, "15 of what is 30?", exploring the mathematical concepts behind it and providing practical applications to solidify your understanding. We'll move beyond a simple answer, uncovering the underlying principles and empowering you with the tools to solve similar problems with confidence.
Introduction: Deconstructing the Problem
The question "15 of what is 30?" presents a classic problem involving fractions, ratios, and proportions. At its core, it asks us to find the whole number (or the "what") from which 15 represents a specific fraction or part. This seemingly basic problem provides a gateway to understanding more complex mathematical concepts, which are vital in various fields, including science, engineering, and finance. We will explore different approaches to solve this, including using fractions, setting up proportions, and applying algebraic methods.
Method 1: Using Fractions
The problem can be expressed as a fraction: 15 is a certain portion of 30. We can represent this unknown portion as 'x', leading to the equation:
15/x = ? (where ? represents the fraction of 30 that 15 represents)
To find the relationship, we need to determine what fraction 15 represents in relation to 30. This is done by setting up a simple fraction: 15/30. Simplifying this fraction, we get 1/2. This tells us that 15 represents half (or 50%) of 30.
Therefore, the answer to the question "15 of what is 30?" is 60. Because 15 is half of 30, doubling 30 gives us the whole number: 30 * 2 = 60
Method 2: Using Ratios
Ratios offer another perspective on solving this problem. A ratio expresses the relationship between two quantities. In this case, the ratio of 15 to 30 can be written as 15:30. This ratio simplifies to 1:2, which again shows that 15 is half of 30.
To find the whole number, we can set up a proportion using the simplified ratio:
1/2 = 30/x
Cross-multiplying, we have:
1 * x = 2 * 30
x = 60
This confirms that 15 is half of 60.
Method 3: Applying Algebra
The problem can also be solved using algebra. Let's represent the unknown number as 'x'. If 15 is a fraction of x and equals 30, we can set up the equation:
(15/x) * x = 30
This simplifies to:
15 = 30/(x/15)
To solve for x, we can use the following steps:
- Multiply both sides by x: 15x = 30
- Divide both sides by 15: x = 30/15 = 2. This shows that 15 is 1/2 (or 50%) of 30 and confirms that the missing number is twice of 30. Thus x = 60
Method 4: Percentage Approach
We can also approach this problem using percentages. If 15 represents a certain percentage of an unknown number and that percentage of the unknown number is 30, then we can set up a simple equation:
Let x be the unknown number. Then, we can say:
(15/x) * 100% = 50% (since 15 is half of 30)
Solving for x:
1500/x = 50 x = 1500/50 x = 30
This indicates that the percentage that 15 represents is 50% of the unknown number. This implies that 30 is 50% of x. Therefore, to find x (the whole number), we can set up the following equation:
0.5x = 30
x = 30 / 0.5 = 60
This again confirms that 15 is half of 60 and that 60 is the number we are searching for.
Expanding the Understanding: Fractions, Ratios, and Proportions
The seemingly straightforward question, "15 of what is 30?", serves as a springboard for exploring broader mathematical concepts:
-
Fractions: A fraction represents a part of a whole. The problem highlights how fractions can be used to express relationships between quantities. Understanding how to simplify fractions is crucial for efficient problem-solving.
-
Ratios: A ratio compares two or more quantities. The ratio 15:30 showcases how ratios can be used to represent relative sizes or proportions. Simplifying ratios to their lowest terms simplifies calculations.
-
Proportions: A proportion is a statement of equality between two ratios. Setting up proportions (like 15/x = 1/2) allows us to solve for unknown quantities. Cross-multiplication is a key technique in solving proportions.
Real-World Applications
The concepts explored above have wide-ranging practical applications:
-
Scaling Recipes: If a recipe calls for 15 grams of sugar and you want to double the recipe, understanding proportions helps you calculate the required amount of sugar (30 grams).
-
Financial Calculations: Calculating percentages (interest rates, discounts, etc.) relies heavily on understanding fractions, ratios, and proportions.
-
Map Scales: Interpreting map scales involves working with ratios and proportions to determine distances in the real world.
-
Mixing Solutions: In chemistry and other sciences, accurately calculating the proportions of different substances in a mixture is crucial.
-
Engineering and Construction: Blueprint interpretation and construction calculations often involve proportional reasoning to scale drawings and plans.
Frequently Asked Questions (FAQs)
-
Q: Is there only one way to solve this problem?
- A: No, there are several methods, as demonstrated above. The best method often depends on personal preference and the complexity of the problem.
-
Q: What if the numbers were more complex?
- A: The same principles apply. Setting up a proportion or using algebraic equations will help solve the problem regardless of the numbers involved.
-
Q: How can I improve my understanding of fractions, ratios, and proportions?
- A: Practice is key! Work through various problems of increasing complexity. Online resources and textbooks offer further practice opportunities.
Conclusion: Mastering the Fundamentals
Solving the seemingly simple problem of "15 of what is 30?" opens a gateway to understanding the fundamental mathematical concepts of fractions, ratios, and proportions. Mastering these concepts is not just about solving mathematical puzzles; it's about developing crucial problem-solving skills applicable to a wide range of real-world situations. By understanding the different methods for solving such problems and practicing regularly, you can build a strong foundation in mathematics and improve your ability to tackle more complex challenges with confidence and ease. The key is to practice consistently and to approach each problem with a clear understanding of the underlying principles. With dedicated effort, anyone can master these core mathematical concepts and unlock their potential in various fields of study and life.
Latest Posts
Latest Posts
-
What Is Equivalent To 2 5
Sep 07, 2025
-
How Tall Is 62 Inches
Sep 07, 2025
-
Tango And Cash The Movie
Sep 07, 2025
-
Inputs And Outputs Of Etc
Sep 07, 2025
-
Average Percentage Alcohol In Beer
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about 15 Of What Is 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.